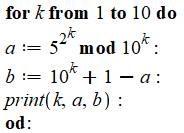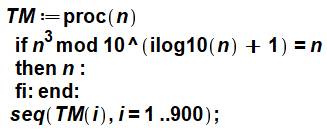collection de nombres, automorphiques, mêmes chiffres dans le carré

NOMBRES – Curiosités, Théorie et Usages

Accueil DicoNombre Rubriques Nouveautés Édition du: 17/06/2022

Orientation générale DicoMot Math Atlas Actualités M'écrire

Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

FORMES des nombres

Débutants

Général

NOMBRES AUTOMORPHES

Glossaire

Général

INDEX

Formes des nombres

Sommaire de cette page

>>> Approche

>>> Automorphes e longueur k

>>> Démonstration

>>> Automorphes généralisés

>>> Trimorphes

NOMBRES AUTOMORPHES

ou nombres circulaires

Motif qui se répète dans le carré.

Exemple: 25² = 625

Nombres N tels que: N² – N = N (N – 1) = 10^k x M

Exemple: 25² – 25 = 25 x 24 = 600

Anglais: Automorphic numbers or circular numbers

Approche

Le carré se termine par le nombre lui-même.

Les deux seuls nombres automorphes inférieurs à 100.

25² = 625

76² = 5 776

90 625² = 8 212 890 625

Voir Nombres plaqués / Nombre 25 / Nombre 76

Construction pour deux chiffres

Si le produit d'un nombre avec son voisin est un multiple de 100, lui ajouter ce nombre.

n (n – 1) = 100k

100k + n

et n (n – 1) – n = n²

76 x 75 = 5700

+ 76 = 5776

et 76² = 5776

Automorphes de longueur k
Pour tout k > 1, il existe deux nombres automorphes avec k chiffres.	Exemple k = 10 8 212 890 625² = 67 451 572 418 212 890 625 1 787 109 376² = 3 193 759 921 787 109 376
Ces nombres se calculent facilement
Programme Python	Programme Maple
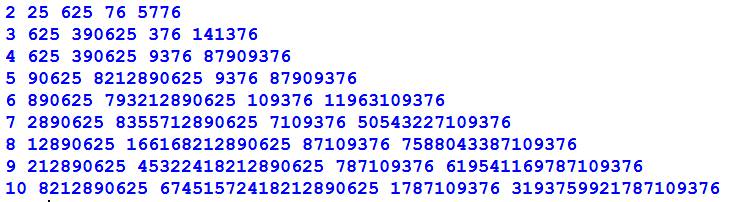
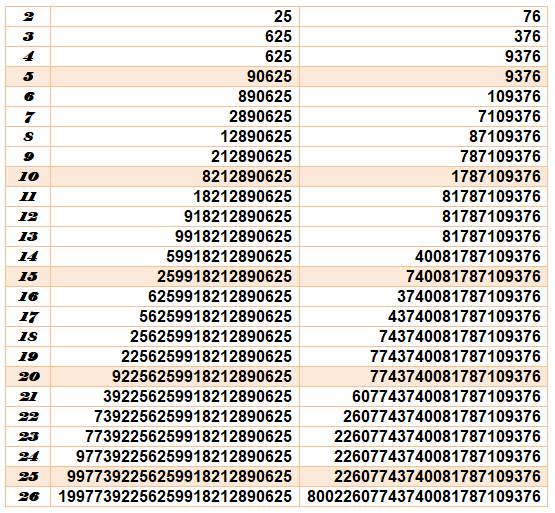
Nombres automorphes de longueur k pour k jusqu'à 10, avec leur carré k, n₅, n₅², n₆, n₆² Note: si le nombre affiche moins de k chiffres, c'est que les premiers sont des 0. Nombres automorphes avec k jusqu'à 26 Notez que chaque nombre est égal au précédent avec un chiffre significatif en plus. Notez aussi que le nombre suivant n'est pas le carré du précédent, mais son carré tronqué (le carré de 390 625 (six chiffres) est 8 212 890 625, on ne conserve que sept chiffres: 890 625). Plus loin 30, 106619977392256259918212890625 51, 574234423230896109004106619977392256259918212890625 Voir Nombres p-adiques Produit nul Le produit de ces deux nombres se termine par autant de zéros que de chiffres dans les opérandes:

Voir Programmation – Index / Brève N° 509

Les automorphes à 2, 3 ou 4 chiffres – Démonstration

Deux chiffres pour a

a² - a doit se terminer par 00 (Ex: 625 – 25 = 600).

a (a – 1) est divisible par 100 = 4 x 25.

Un des facteurs est multiple de 4 et l'autre de 25.

Si a = 25k, alors a – 1 = 25k – 1 = 4h; seule possibilité pour k = 1.

Une des solutions est: a = 25 et a² = 625.

Si a – 1 = 25k, alors a = 25k + 1 = 4h; seule possibilité pour k = 3

L'autre solution est: a = 75 + 1 = 76 et a² = 5 776

Trois chiffres pour a

a (a – 1) est divisible par 1000 = 8 x 125.

Si a = 125k, alors a – 1 = 125k – 1 = 8 x 15k + (5k – 1) = 8h. Il faut que 8 divise 5k – 1. Seule possibilité avec k = 5. et a = 625.

Si a – 1 = 125k, alors a = 125k + 1= 8 x 15k + (5k + 1) = 8h. Seule possibilité k = 3 et a = 376.

Quatre chiffres pour a

a (a – 1) est divisible par 10 000 = 16 x 625.

Si a = 625k, alors a – 1 = 625k - 1 = 624k + (k – 1) = 16h. k = 17 et a = 10 625 qui a plus de quatre chiffres

Si a – 1 = 625 k, alors a = 625k + 1 = 624k + (k + 1) = 16h. k = 16 et a = 9 376, la seule solution.

Nombres automorphes – Généralisation

Définition

Un nombre n,
tel que les derniers chiffres de a.n²sont identiques à n,
est automorphe d'ordre égal à a.

Ex: 88² x 2 = 15 488

Ordre 1

N	*N² avec 5*	*N² avec 6*
5	25
6		36
25	625
76		5 776
376		141 376
625	390 625
9 376		87 909 376
90 625	8 212 890 625

Ordre a

a	N	*a.N²*
1	8	128
2	88	15 488
3	6 666 666 667	133 333 333 346 666 666 667
5	3 642 578 125	66 341 876 983 642 578 125
9	8 888 888 889	711 111 111 128 888 888 889

NOMBRES TRIMORPHES

Définition

Un nombre n tel que
les derniers chiffres de n³sont identiques à n
est trimorphe.

Exemples

N³

125

249

251

375

376

499

125

216

729

13 824

15 625

117 649

132 651

421 875

438 976

970 299

1 953 125

15 438 249

15 813 251

52 734 375

53 157 376

124 251 499

Commentaires

On calcule la longueur du nombre avec le logarithme à base 10.
On teste les derniers chiffres avec un calcul modulo.

La séquence appelle la procédure pour les nombres de 1 à 900.

Résultat du traitement en bleu.

Voir Programmation – Index

Liste jusqu'à 10 000

1, 4, 5, 6, 9, 24, 25, 49, 51, 75, 76, 99, 125, 249, 251, 375, 376, 499, 501, 624, 625, 749, 751, 875, 999, 1249, 3751, 4375, 4999, 5001, 5625, 6249, 8751, 9375, 9376, 9999.

Nombre tri-automorphe (suite)

On retrouve le nombre initial en fin de 3n²
Il en existe 3 pour les nombres à 4 chiffres.

N	N²	3N²
6 667	44 448 889	133 346 667
6 875	47 265 625	141 796 875
9 792	95 883 264	287 649 792

D'une manière générale, il y en a 3 pour tous les nombres à n chiffres.

6666666667	44444444448888888889	133333333346666666667
7262369792	52742014995754123264	158226044987262369792
9404296875	88440799713134765625	265322399139404296875

Suite	Nombres plaqués Répétition des chiffres dans les puissances Dizaine et unité des nombres et leurs puissances
Même type de sujets en	Terminaison des produits Terminaison des puissances Produits amusants en puissances de 2 et de 5
Voir	Facteurs sans zéro Motifs Nombre 6 667 Nombres ABA Palindromes Pannumériques
Site	Nombres automorphes – Wikipédia Automorphic number – Wolfram MathWorld OEIS A033819 - Trimorphic numbers: n^3 ends with n
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/Automorf.htm