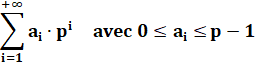|
Édition du: 15/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Introduction Nombres spécifiques, basés sur les nombres premiers (p), qui
propulsent les mathématiciens dans un monde nouveau, comme l'avait fait les nombres
complexes. Ils ont été inventés en 1897 par Kurt Hensel
(1861-1941). Leurs propriétés sont si fascinantes que de nombreux mathématiciens
en font leur quotidien pour explorer les profondeurs de la théorie
des nombres. Les nombres p-adiques sont déroutants: écriture des décimales à
gauche, pas de signe moins, nouvelle manière pour mesurer la proximité entre
nombres, somme de séries qu'on pourrait croire divergente, topologie
déroutante (convergence), etc. |
||
|
|
Sommaire de cette page >>> Approche >>> La formation des p-adiques >>> Un nouvel ensemble de nombres >>> Solution des équations >>> Historique: Kurt HENSEL >>> Bilan |
Débutants Glossaire |
|
Français |
Anglais |
|
P-adique |
P-adic |
|
Décadique |
Decadic |
|
Brenom |
Leftist |
|
Dyadique |
Dyadic |
|
Triadique |
Triadic |
|
Automorphe |
Automorphic |
En bref, un aperçu
|
Les nombre p-adiques sont les gauchers dans le monde des nombres. Ils sont
tous de l'autre côté. Comme dans un miroir. En anglais, ils sont nommés leftists (gauchers) et en français brenoms (nombres en verlan). |
|
Voir Nombres
retournés
Intention
|
Compléter
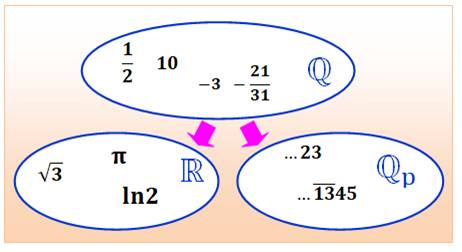
les nombres rationnels ℚ par une nouvelle race de nombres, les p-adiques ℚp, Comme ils
sont complétés pour les réels ℝ. |
|
|
Idée originale ! Les
chiffres des nombres ordinaires (entiers, réels)
se prolongent à l'infini vers la droite. Ils sont en quantité finie à gauche. |
5 =
5,000… 5/2 =
2,500… 1/3 =
0,333… |
|
|
Pourquoi ne pas les prolonger vers
la droite On invente un nouveau type de nombres: à l'image
des nombres ordinaires, sans autres indications, les chiffres de ces nombres
sont nuls à gauche (au lieu de la droite). Ou alors répétitif à l'infini. La période est
signalée par une parenthèse; |
Nombres entiers et rationnels …5 =
…0005 = (0)5 …5,25 =
…0005,25 = (0)5,25 Nombres périodiques …3335 =
…(3)5 ...
3335,18 = …(3)5,18 Notations de la période
Nombres réels …324598,1265 |
|
|
Pas si farfelu ! On obtient ainsi une théorie algébrique complète,
dite p-adique, qui a certaines propriétés
un peu plus simples que l’algèbre avec les nombres ordinaires. Outre une étude de mathématique pure, cette
théorie des nombres p-adiques est utilisée pour se projeter dans un nouveau monde où les propriétés des nombres
ordinaires sont plus faciles à démontrer. En base 10,
ces nombres sont semblables aux nombres ordinaires; on les nomme décadiques ou 10-adiques ou encore
brenoms (nombres en verlan). |
Les mathématiciens utilisent souvent de tels artifices pour contourner
certaines difficultés.
|
|
|
Dans le cas des congruences avec les nombres
ordinaires ou les p-adiques, on travaille dans un monde restreint, en tout
cas limité, et ensuite, on repasse au monde des réels où l'espace est infini. |
Principe général – local
– général, ou global – local –
global, ou infini – fini –
infini |
|
Voir Brève
890
|
Nombre rationnels (fractions) Sur la droite des
nombres, les nombres rationnels
occupent des positions discrètes. Il existe des espaces (des trous) entre
tous ces nombres. |
5, 13,
22/7, 0,333… |
||
|
Nombres réels Avec les nombres réels,
on remplit la droite
des nombres. Certains des nombres ultimes (quantité infinie de
décimales non répétitives) ont un nom. |
3; 3,1;
3,14; 3,11415; … Pi |
||
|
Proximité: notion de distance Cette notion de distance
est nécessaire pour situer les nombres entre eux. Avec les nombre réels, il s'agit de la valeur
absolue de la différence. |
Deux nombres réels
sont d'autant plus proches qu'ils partagent leurs chiffres de grands poids. |
||
|
Nombres p-adiques Semblable aux nombres réels mais avec une notion
de proximité différence; elle est inversée. |
Deux nombres sont d'autant plus proches qu'ils partagent
leurs chiffres de petits poids. 0,03; 0,53; 6,53;
96,53; 196,53; 1196,53;
21196,53 sont de plus en plus
proches en p-adique. |
||
|
Nombres gauchers (leftist numbers)
ou brenoms Nombres qui peuvent s'écrire avec une infinité de
chiffres à gauche et une quantité limitée à droite. |
…21196,53 est 10-adique Note: un p-adique suppose une base
de numération égale à un nombre
premier. Un nombre 10-adique (décadique) n'est pas, à proprement parler,
un p-adique. |
||
|
Les nombres entiers sont connus et vénérés par
les Pythagoriciens
dès le VIe siècle avant notre ère. Mille ans plus tard, ils sont complétés par le zéro en
provenance d'Inde. |
Le zéro marque la frontière entre les entiers
positifs et les entiers négatifs. |
|
|
Les entiers signés forment l'ensemble des entiers
relatifs
ℤ. C'est un
ensemble discret (composé d'éléments individuels). Il possède une structure d'anneau
car il est stable pour l'addition, la
soustraction et la multiplication. |
Autrement-dit le résultat des opérations reste un
entier relatif. |
|
|
Pour passer à la division
et former un corps,
il faut considérer les fractions et former l'ensemble des nombres rationnels ℚ. |
Ce corps qui
permet les quatre opérations est plus compact mais reste encore discret (avec
des "trous"). |
|
|
C'est avec les nombres réels ℝ que l'ensemble
devient continu. On y trouve désormais tous les nombres irrationnels
et transcendants. |
Ce corps est continu. Il présente encore un
inconvénient, il n'autorise pas la division par zéro. |
|
|
Une idée géniale: l'étude des nombres par leurs
restes de la division: congruences. |
Outil très puisant, mais le zéro reste un
inconvénient
|
|
|
Encore mieux: les nombre p-adiques (p est
premier) cochent toutes les cases et offrent de nombreuses autres propriétés intéressantes. |
Corps (quatre opérations) Continu (extension des nombres réels) Pas de diviseurs de zéro à condition que p soit
bien un nombre premier. |
|
|
Les nombres p-adiques offrent de nouvelles
solutions à certaines équations. |
||
|
Théorème fondamental de l'algèbre La quantité de
racines complexes d'un polynôme est égale à son degré. |
Ce n'est pas le cas en
décadiques (ℚ10). |
|
|
Exemple x² – x = 0 Deux solutions évidentes 0 et 1. C'est tout, Non
! |
En p-adiques, il y en a deux
autres (u, v). |
|
|
Les deux autres racines (u et v) présentent les relations
habituelles des racines d'une équation du
second degré. |
u + v = 1 u · v = 0 |
|
|
Si x² = x, ces deux nombres partagent au moins
les mêmes unités |
5² = 25 & 6²
= 36 Les deux seuls nombres à un
chiffre ayant cette propriété d'automorphisme.
|
|
|
Il est tout à fait possible de poursuivre les
recherches avec les dizaines puis les centaines, etc. |
25² = 625 et 76² = 5 776 |
|
|
Après plusieurs itérations: Hors les unités, les chiffres de même rang se
complémentent à 9 pour u et v. La somme vaut 1 en 10-adique. Autre propriété qui justifie sa présence sur
cette page consacrée aux p-adiques: son produit limité à la quantité de
chiffres des opérandes reste nul. Conséquence, pour éviter ce
phénomène de produit nul et de division par zéro, les p-adiques ont toujours une base p première. |
u = …12 890 625 v = … 87 109 376 u + v = …00
000 001 u·v = …00 000 000 Voir Nombres
automorphes |
|
|
De tels nombres (u et v) qui se prolongent sans
fin à gauche sont des nombres décadiques automorphes. Ce phénomène n'existe pas pour le p-adiques avec
p premier. |
Le fait que le produit de ces
deux nombres est nul montre que (ℚ10) n'est pas intégre: hors 0 et
1, car il existe des nombres dont le produit est nul.
|
|
|
Leonhard Euler
(1717-1783) montre que les séries à progression
géométrique (séries entières) convergent vers une valeur, même si la
raison n'est pas comprise entre -1 et 1. En donnant un
sens à ce résultat non conventionnel, la postérité construira les nombres
p-adiques. Kurt Hensel
(1861-1941) est un mathématicien allemand (prussien). Né à Königsberg
(Kaliningrad) et mort à Marbourg en Allemagne.
1897: invention des nombres p-adiques présentés
dans un article étudiant les nombres algébriques. Il s'inspire des travaux de
Ernst Kummer et Richard Dedekind sur la factorisation des nombres. Hensel, élève de Koneker, étudie la
représentation des nombres entiers par des séries entières (power series) du
type:
Ce sont des séries qui n'ont pas de sens
mathématiques mais qui permettent d'effectuer des calculs. Notion de corps
muni d'une valuation. Nombreux résultats sur les formes quadratiques et en théorie des
nombres. 1913: Kürschàk généralise la notion de valuation. 1921 ou 1923:
Le mathématicien Helmut Hasse, travaillant avec Hensel, met en
évidence la richesse des nombres p-adiques. Il prouve que: Une forme
quadratique a une racine rationnelle si et seulement si elle a une solution
dans le corps des nombres p-adiques pour tout nombre premier p ainsi qu'une
solution réelle. Suite: Développements modernes Anglais: Hensel invented
the p-adic numbers, an algebraic theory which has proved important in later
applications.
|
Voir Contemporains
|
Si p est premier, l'ensemble des entiers relatifs p-adiques n'a pas de
diviseurs de zéro. C'est une des raisons pour s'intéresser aux –adiques. |
|
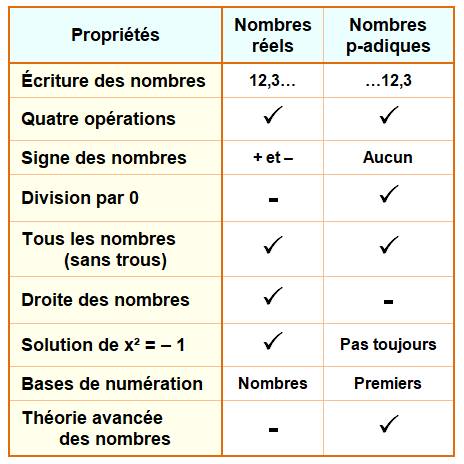
Résumé des propriétés
comparées
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
|
|
|
Cette page |