NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suite de nombres
Débutants Général	Itérations – Cycles			Glossaire Suites et Séries
INDEX Rubriques	Cycle de Syracuse	Procédé de Kaprekar	Cycle des Carrés
	Syracuse – Débutant	Sommaire de cette page >>> Record de durée de vol >>> Record d'altitude >>> Suites de Syracuse pour tous les nombres de 1 à 50 >>> Tables des séquences enchaînées pour tous les nombres de 0 à 102
	Syracuse – développement
	Syracuse - variantes
	Syracuse – algèbre (2^x3^y)
	Syracuse – Tables
	Syracuse et nombre 27
	Syracuse – Programmation

Record de durée de vol
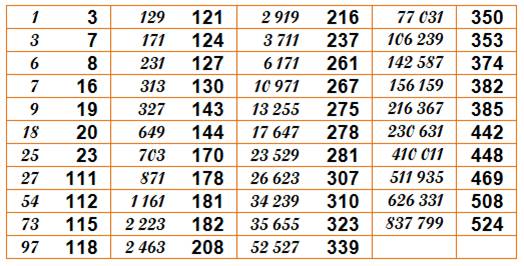
La durée de vol est le nombre d'étapes pour passer de n à 1: Avec 3, il faut sept étapes: 10, 5, 16, 8, 4, 2, 1. La table donne la valeur de n pour des durées de vol de plus en pus grande. Nombres record en durée de vol et leur enchainement Chaque cycle est tronqué dès que le nombre du cycle est déjà apparu dans un cycle record précédent. Le cycle du nombre 9 est stoppé à la rencontre du nombre 22, présent dans le cycle de 7. [3, 10, 5, 16, 8, 4, 2, 1] [6, 3, 10] [7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10] [9, 28, 14, 7, 22], [18, 9, 28], 28 [25, 76, 38, 19, 58, 29, 88, 44, 22] [27, 82, 41, 124, 62, 31, 94, 47, …, 121, 364, 182…160, 80, 40] [54, 27, 82] [73, 220, 110, 55, 166, 83, 250, 125, 376, 188, 94] [97, 292, 146, 73, 220] [129, 388, 194, 97, 292] [171, 514, 257, 772, 386, 193, 580, 290, 145, 436, 218, 109, 328, 164, 82] [231, 694, …, 391, 1174, 587, …, 248, 124] [313, 940, …, 1456, 728, 364] [327, 982, …, 1000, 500, 250] [649, 1948, …, 4696, 2348, 1174] [703, 2110, 1055, …, 4009, 12028, 6014, …304, 152, 76] [871, 2614, 1307, 3922, … 1196, 598], 190996 [1161, 3484, 1742, 871, 2614] [2223, 6670, …, 24056, 12028] [2463, 7390, …, 9355, 28066, 14033, …, 1406, 703, 2110] [2919, 8758…, 112264, 56132, 28066] [3711, 11134, …, 1034, 517, 1552, 776, 388] [6171, 18514, … 1379, 4138, 2069, 6208, 3104, 1552] Altitude maximale pour ces nombres avec record de durée On retrouve souvent les mêmes valeurs. Ce qui veut dire que les cycles en question se rejoignent en ce point là ou bien avant. Lecture: Nombre, altitude maximale, atteinte au rang indiqué.
3, 16, 4 6, 16, 5 7, 52, 6 9, 52, 9 18, 52, 10 25, 88, 7 27, 9232, 78 54, 9232, 79	73, 9232, 82 97, 9232, 85 129, 9232, 88 171, 9232, 91 231, 9232, 94 313, 9232, 97 327, 9232, 110 649, 9232, 111	703, 250504, 83 871, 190996, 32 1161, 190996, 35 2223, 250504, 95 2463, 250504, 121 2919, 250504, 129 3711, 481624, 25 6171, 975400, 79

Record d'altitude

Les quatre premiers records

Le nombre 3 entraine une montée jusqu'à 16 dés la troisième étape (rang 4) sur les sept du cycle. Avec 7, un nouveau record avec 52 obtenu à la septième étape (rang 8) sur dix-sept.

Exemples

2	1
3	10	5	16	8	4	2	1
7	22	11	34	17	52	26	13	40
15	46	23	70	35	106	53	160	80

Liste des records [nombre au départ, longueur du cycle, rang du maximum, valeur du maximum]

[2, 1, 1, 2] [3, 7, 4, 16] [7, 16, 6, 52] [15, 17, 8, 160] [27, 111, 78, 9 232] [255, 47, 16, 13 120] [447, 97, 54, 39 364] [639, 131, 26, 41 524] [703, 170, 83, 250 504] [1 819, 161, 51, 1 276 936] [4 255, 201, 86, 6 810 136] [4 591, 170, 60, 8 153 620] [9 663, 184, 49, 27 114 424] [20 895, 255, 88, 50 143 264] [26 623, 307, 64, 106 358 020] [31 911, 160, 77, 121 012 864] [60 975, 334, 117, 593 279 152] [77 671, 231, 72, 1 570 824 736]

[113 383, 247, 121, 2 482 111 348] [138 367, 162, 72, 2 798 323 360] [159 487, 183, 67, 17 202 377 752] [270 271, 406, 212, 24 648 077 896] [66 5215, 441, 145, 524 83 285 312] [704 511, 242, 70, 56 991 483 520] [1 042 431, 439, 225, 90 239 155 648] [1 212 415, 328, 85, 139 646 736 808] [1 441 407, 367, 142, 151 629 574 372] [1 875 711, 370, 132, 155 904 349 696] [1 988 859, 427, 145, 156 914 378 224] [2 643 183, 430, 202, 190 459 818 484] [2 684 647, 399, 121, 352 617 812 944] [3 041 127, 363, 79, 622 717 901 620] [3 873 535, 322, 128, 858 555 169 576] [4 637 979, 573, 169, 1 318 802 294 932] [5 656 191, 400, 171, 2 412 493 616 608]

Programme Maple

But

Détecter les maximums dans la suite de Syracuse et établir la liste des records.

Commentaires

Record en cours placé en rmx.

Boucle en k avec un max de 10 000 et arrêt par break dès que la fin en 1 est détectée.

La liste L contient tout le vol de la suite. L'ensemble S reprend cette liste en l'ordonnant. Le plus grand nombre en fin de liste S[-1] est détecté et mis en mx.

Search est utilisé pour donner le rang de mx dans la liste L.

Si cette valeur est supérieure au record enregistré rmx, cette nouvelle valeur est placée dans la liste A.

En fin de programme, impression de la liste A.

Voir Programme cycle de Syracuse / Programmation – Index

SUITES DE SYRACUSE

pour tous les nombres de 1 à 50

Légende

5	5	16	5	[1	2	4	8	16	5]
n nombre de départ	longueur de la suite ou temps de vol	valeur maximum dans la suite ou hauteur de vol	longueur de la suite pour atteindre la hauteur maximum	Suite de Syracuse En jaune: nouveaux nombres

1	0	0	0	[1]
2	1	1	1	[1	2]
3	7	16	5	[1	2	4	8	16	5	10	3]
4	2	2	2	[1	2	4]
5	5	16	5	[1	2	4	8	16	5]
6	8	16	5	[1	2	4	8	16	5	10	3	6]

7	16	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7]
8	3	4	3	[1	2	4	8]
9	19	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	9]
10	6	16	5	[1	2	4	8	16	5	10]
11	14	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11]
12	9	16	5	[1	2	4	8	16	5	10	3	6	12]
13	9	40	9	[1	2	4	8	16	5	10	20	40	13]
14	17	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14]
15	17	160	11	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	15]
16	4	8	4	[1	2	4	8	16]
17	12	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17]
18	20	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	9	18]
19	20	88	18	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19]
20	7	16	5	[1	2	4	8	16	5	10	20]

21	7	64	7	[1	2	4	8	16	32	64	21]
22	15	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22]
23	15	160	11	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23]
24	10	16	5	[1	2	4	8	16	5	10	3	6	12	24]

25	23	88	18	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19	38	76	25]
26	10	40	9	[1	2	4	8	16	5	10	20	40	13	26]

27	111	9232	35	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	92	184	61	122
	244	488	976	325	650	1300	433	866	1732	577	1154	2308	4616	9232	3077	6154	2051	4102	1367	2734	911	1822	3644	7288
	2429	4858	1619	3238	1079	2158	719	1438	479	958	319	638	1276	425	850	283	566	1132	377	754	251	502	167	334
	668	1336	445	890	1780	593	1186	395	790	263	526	175	350	700	233	466	155	310	103	206	412	137	274	91
	182	364	121	242	484	161	322	107	214	71	142	47	94	31	62	124	41	82	27]

28	18	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28]
29	18	88	18	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29]
30	18	160	11	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	15	30]

31	106	9232	35	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	92	184	61	122
	244	488	976	325	650	1300	433	866	1732	577	1154	2308	4616	9232	3077	6154	2051	4102	1367	2734	911	1822	3644	7288
	2429	4858	1619	3238	1079	2158	719	1438	479	958	319	638	1276	425	850	283	566	1132	377	754	251	502	167	334
	668	1336	445	890	1780	593	1186	395	790	263	526	175	350	700	233	466	155	310	103	206	412	137	274	91
	182	364	121	242	484	161	322	107	214	71	142	47	94	31]

32	5	16	5	[1	2	4	8	16	32]
33	26	100	26	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19	38	76	25	50	100	33]
34	13	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34]
35	13	160	11	[1	2	4	8	16	5	10	20	40	80	160	53	106	35]
36	21	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	9	18	36]
37	21	112	21	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	56	112	37]
38	21	88	18	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19	38]
39	34	304	25	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19	38	76	152	304	101	202	67	134	268	89	178	59	118	39]
40	8	20	8	[1	2	4	8	16	5	10	20	40]

41	109	9232	35	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	92	184	61	122
	244	488	976	325	650	1300	433	866	1732	577	1154	2308	4616	9232	3077	6154	2051	4102	1367	2734	911	1822	3644	7288
	2429	4858	1619	3238	1079	2158	719	1438	479	958	319	638	1276	425	850	283	566	1132	377	754	251	502	167	334
	668	1336	445	890	1780	593	1186	395	790	263	526	175	350	700	233	466	155	310	103	206	412	137	274	91
	182	364	121	242	484	161	322	107	214	71	142	47	94	31	62	124	41]

42	8	64	7	[1	2	4	8	16	32	64	21	42]
43	29	196	27	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	56	112	37	74	148	49	98	196	65	130	43]
44	16	52	12	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44]
45	16	136	16	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	68	136	45]
46	16	160	11	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46]

47	104	9232	35	[1	2	4	8	16	5	10	20	40	80	160	53	106	35	70	23	46	92	184	61	122
	244	488	976	325	650	1300	433	866	1732	577	1154	2308	4616	9232	3077	6154	2051	4102	1367	2734	911	1822	3644	7288
	2429	4858	1619	3238	1079	2158	719	1438	479	958	319	638	1276	425	850	283	566	1132	377	754	251	502	167	334
	668	1336	445	890	1780	593	1186	395	790	263	526	175	350	700	233	466	155	310	103	206	412	137	274	91
	182	364	121	242	484	161	322	107	214	71	142	47]

48	11	24	11	[1	2	4	8	16	5	10	3	6	12	24	48]
49	24	148	24	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	7	14	28	56	112	37	74	148	49]
50	24	88	18	[1	2	4	8	16	5	10	20	40	13	26	52	17	34	11	22	44	88	29	58	19	38	76	25	50]

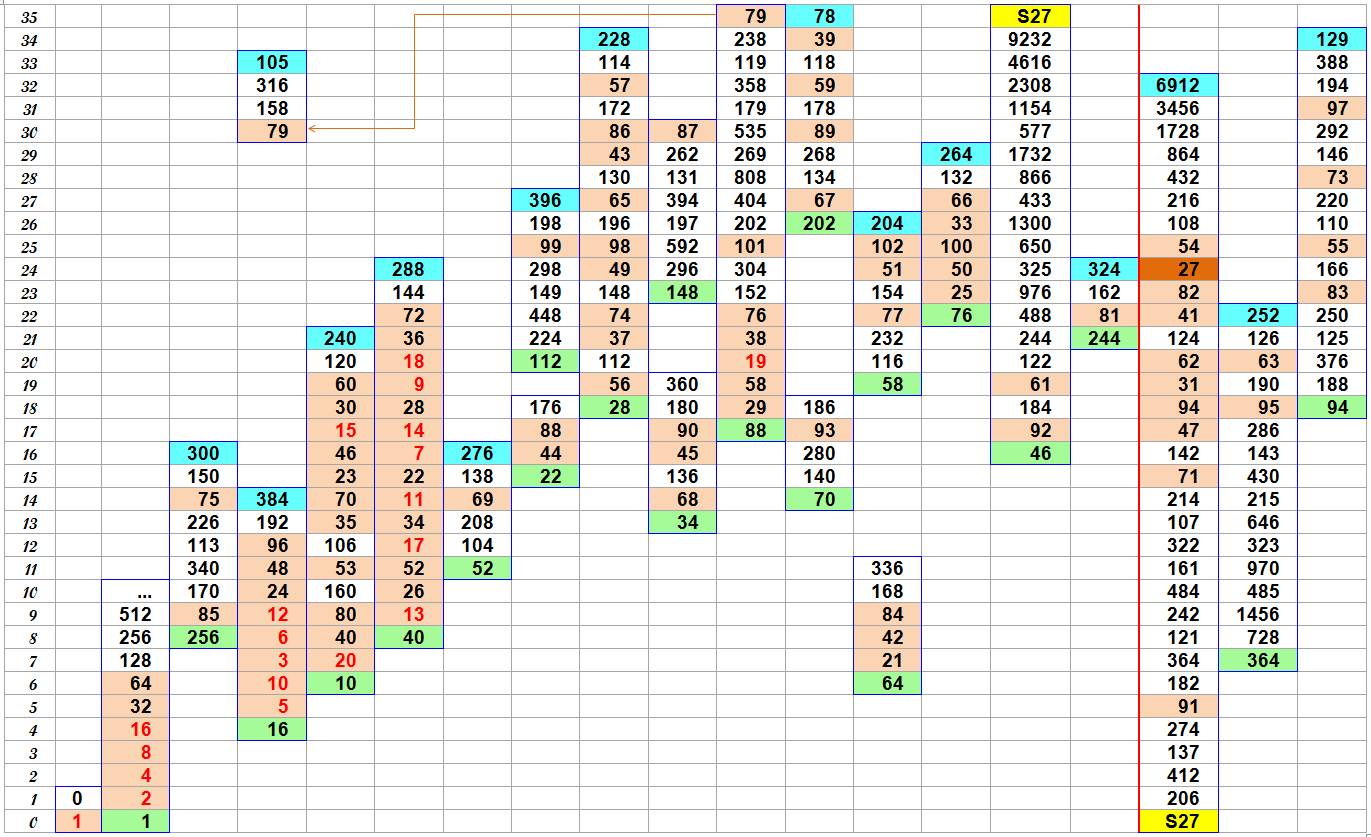
Table des séquences enchaînées pour tous les nombres de 0 à 102.

Une colonne représente une séquence élémentaire comme: 512, 256, 128 … Le pied de séquence en vert indique que ce nombre est déjà présent dans une colonne à gauche (ou droite exceptionnellement). Exemple: 300 …170, 85, 256, => 256, 128 … Les nombres de 0 à 20 sont repérés en rouge. La séquence dite du nombre 27 (27 en marron) part dans la colonne 3 à partir de la droite se poursuit en S27 en tête de colonne 5 à partir de la droite; entre les deux cases notés S27 se trouve la cinquantaine d'autres nombres non représentés. En tête de séquence, en bleu, des nombres divisibles par 3. Ils sont issus d'une division par 2 mais jamais de l'opération 3n +1. Un multiple de 3 moins 1 n'est jamais divisible par 3.

Voir Présentation en arbre

Retour	Cycle de Syracuse Syracuse – algèbre (2^x3^y)
Voir	Syracuse et nombre 27 Syracuse – Programmation
Sites	Voir Liste en page d'introduction
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Syracus1.htm