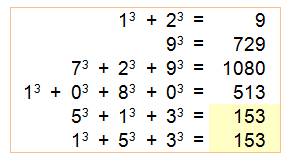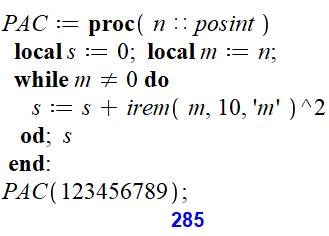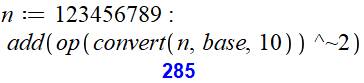|
|||||||||||||||||||||||||||||||||
![]()
|
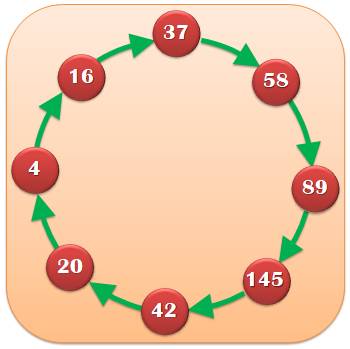
Racine additive carrée Suite en boucle avec des carrés Nombres heureux Le cycle dit de Syracuse est bien curieux. Voici un autre cycle étrange,
finissant toujours sur les mêmes chiffres 1 ou 4. Avec les carrés, ce sont des boucles qui
apparaissent.
Bons sujets pour des travaux
de découverte des nombres avec des élèves. Notez que sans l'élévation au carré des chiffres, on a la racine
numérique des nombres. |
Anglais: happy and sad numbers,
sometimes called friendly numbers
|
|
|
|
Merci à Amine
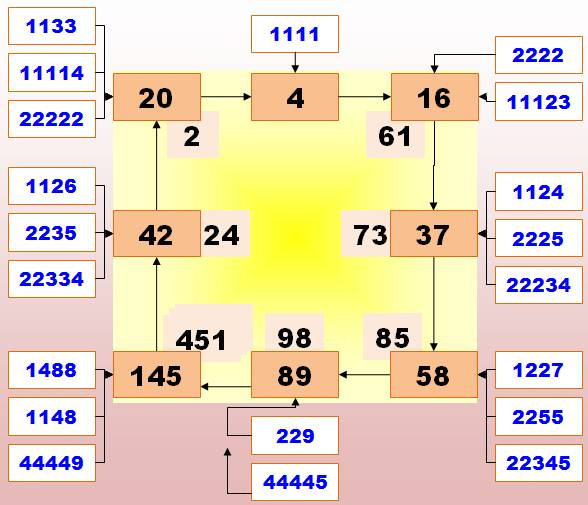
Boucle
et son voisinage
|
|
Remarque
|
En
prenant la somme des chiffres, et non pas celle de leur carré, nous aurions
la racine numérique du nombre qui prend
les valeurs de 0 à 9. |
Voir Racine
numérique / Preuve par
neuf / Divisibilité par 3
|
|
|
|
|
|
|
|
|
|
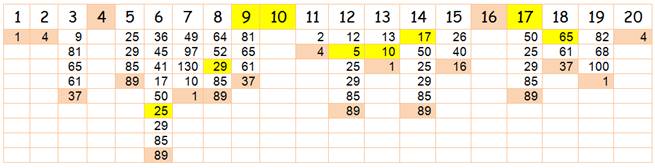
La
même liste complète pour chaque nombre Nombre,
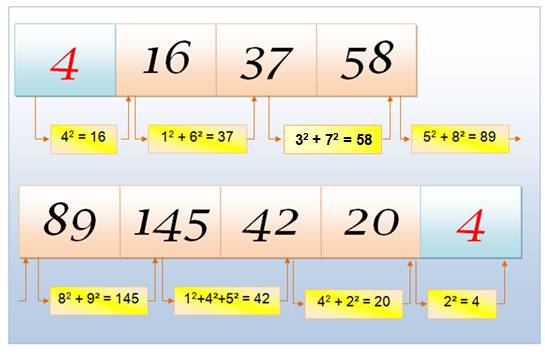
[somme des carrés des chiffres], quantité d'itérations 1, [1], 1 2, [4, 16, 37, 58, 89, 145, 42, 20, 4], 9 3, [9, 81, 65, 61, 37, 58, 89, 145, 42, 20, 4], 11 4, [16, 37,
58, 89, 145, 42, 20, 4], 8 5, [25, 29, 85, 89, 145, 42, 20, 4], 8 6, [36, 45, 41, 17, 50, 25, 29, 85, 89, 145, 42, 20,
4], 13 7, [49, 97, 130, 10, 1], 5 8, [64, 52, 29, 85, 89, 145, 42, 20, 4], 9 9, [81, 65, 61, 37, 58, 89, 145, 42, 20, 4], 10 10, [1], 1 11, [2], 1 12, [5, 25, 29, 85, 89, 145, 42, 20, 4], 9 13, [10, 1], 2 14, [17, 50, 25, 29, 85, 89, 145, 42, 20, 4], 10 15, [26, 40, 16, 37, 58, 89, 145, 42, 20, 4], 10 16, [37, 58, 89, 145, 42, 20, 4], 7 17, [50, 25, 29, 85, 89, 145, 42, 20, 4], 9 18, [65, 61, 37, 58, 89, 145, 42, 20, 4], 9 19, [82, 68, 100, 1], 4 20, [4], 1 En ocre,
les itérations qui se terminent par 1. |
|
|
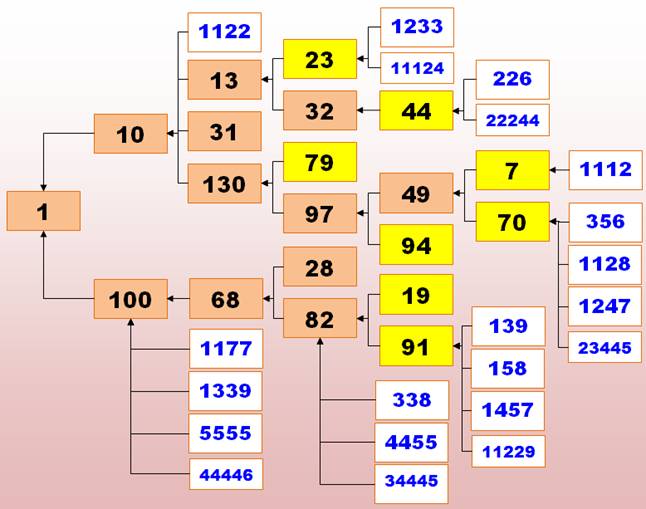
La
somme itérée des carrés des chiffres des nombres conduit
|
|
|
|
|
1, 7,
10, 13, 19,
23, 28, 31,
32, 44, 49,
68, 70, 79,
82, 86, 91,
94, 97, 100,
103, 109, 129,
130, 133, 139,
167, 176, 188,
190, 192, 193,
203, 208, 219,
226, 230, 236,
239, 262, 263,
280, 291,
293, 301, 302,
310, 313, 319,
320, 326, 329,
331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496, 536, 556, 563, 565, 566, 608, 617, 622, 623, 632, 635, 637, 638, 644, 649, 653, 655, 656, 665, 671, 673, 680, 683, 694, 700, 709, 716, 736, 739, 748, 761, 763, 784, 790, 793, 802, 806, 818, 820, 833, 836, 847, 860, 863, 874, 881, 888, 899, 901, 904, 907, 910, 912, 913, 921, 923, 931, 932, 937, 940, 946, 964, 970, 973, 989, 998, 1000, 1003, 1009, … |
|
|
|
|
|
Nombres atteignant une quantité d'itérations
supérieures à celles trouvées jusqu'à là. 1,
[1], 1 2, [4, 16, 37, 58, 89, 145, 42, 20, 4], 9 3, [9,
81, 65, 61, 37, 58, 89, 145, 42, 20, 4], 11 6,
[36, 45, 41, 17, 50, 25, 29, 85, 89, 145, 42, 20, 4], 13 88,
[128, 69, 117, 51, 26, 40, 16, 37, 58, 89, 145, 42, 20, 4], 14 269, [121,
6, 36, 45, 41, 17, 50, 25, 29, 85, 89, 145, 42, 20, 4], 15 15999, [269, 121, 6, 36, 45, 41, 17, 50, 25, 29, 85,
89, 145, 42, 20, 4], 16 Aucun autre jusqu'à 1 million. Soit un record de 16
itérations pour 15 999. Le plus grand avec chiffres non répétés: 986 543 210 (pannumérique) |
|
|
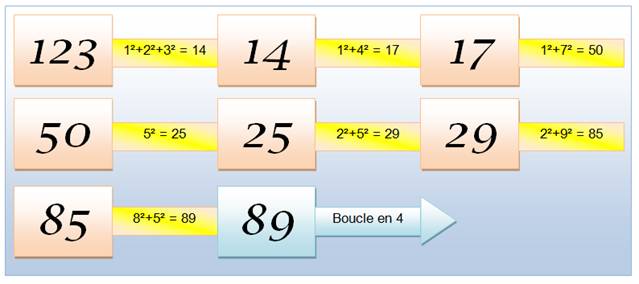
En partant de 12
(exemple), formation d'une boucle avec 153, un nombre narcissique. En partant de 2 et en
sept itérations, ça boucle sur 371, un autre narcissique. |
|
|
|
|
|
Chaque
nombre et ses permutations sont des nombres heureux. On indique
le plus petit et le plus grand. [1,
1], [13, 31], [23, 32], [236, 632], [356, 653], [12456, 65421], [3456, 6543],
[123456, 654321], [7, 7], [1247, 7421], [12347, 74321], [1257, 7521], [1457,
7541], [2457, 7542], [13457, 75431], [23457, 75432], [167, 761], [367, 763],
[24567, 76542], [234567, 765432], [28, 82], [12348, 84321], [1258, 8521],
[12358, 85321], [2458, 8542], [68, 86], [368, 863], [23468, 86432], [123468,
864321], [2568, 8652], [12568, 86521], [123568, 865321], [478, 874], [1478,
8741], [2478, 8742], [13478, 87431], [1578, 8751], [234578, 875432],
[1235678, 8765321], [45678, 87654], [2345678, 8765432], [19, 91], [129, 921],
[139, 931], [239, 932], [49, 94], [2369, 9632], [469, 964], [34569, 96543],
[79, 97], [379, 973], [124579, 975421], [1679, 9761], [13679, 97631],
[134679, 976431], [15679, 97651], [145679, 976541], [24589, 98542], [3689,
9863], [235689, 986532], [245689, 986542], [12345689, 98654321], [3789,
9873], [123789, 987321], [34789, 98743], [5789, 9875], [145789, 987541],
[245789, 987542], [6789, 9876], [36789, 98763], [3456789, 9876543] Les
plus grands nombres heureux croissants
à k chiffres. 7, 97, 973, 9 876,
98 763, 987 542, 9 876 543, 98 654 321 Aucun
n'est pannumérique
(tous les chiffres une fois). Le
plus grand dans l'ordre croissant:
12 345 689 |
|
Voir Nombre
12 345 689 / Nombre
98 654 321
|
|
|
|
A number is said to
be happy, for on finding the sum of the
squares of its digits, and then the sum of the squares of the digits of that
sum, and so on, the process ends in 1. Numbers which do
not end in 1 after the process are said to be sad. |
|
Voir Anglais
|
|
||
|
102, [5, 25, 29, 85, 89, 145, 42,
20, 4], 9 104, [17, 50, 25, 29, 85, 89, 145,
42, 20, 4], 10 105, [26, 40, 16, 37, 58, 89, 145,
42, 20, 4], 10 106, [37, 58, 89, 145, 42, 20, 4],
7 107, [50, 25, 29, 85, 89, 145, 42,
20, 4], 9 108, [65, 61, 37, 58, 89, 145, 42,
20, 4], 9 |
Commentaires Un premier sous-programme (procédure ou fonction)
calcule la somme des carrés des chiffres d'un nombre n. Le nombre est converti en base 10 pour disposer des
chiffres dans la liste N. On ajoute le carré de chacun, du premier au
dernier (nops(N)). La somme est disponible
comme résultat de ce programme. Le programme principal exécute une boucle de
recherche sur les nombres de 100 à 110 par exemple. Le premier résultat du calcul de la somme des
carrés des chiffres (PAC) est placé dans la liste L. Un compteur témoigne de
ce résultat (kt mis à 1). Tant que l'itération ne donne ni 4 ni 1, on
poursuit le travail. Calcul de la nouvelle somme, incrémentation du
compteur d'itérations et mise en liste de ce résultat. Prudent, on évite une recherche qui dépasserait
les 100 itérations (break). Ici, on demande (par exemple) de ne sortir que
les nombres avec plus de 5 itérations. |
|
|
Variante de la procédure
|
Commentaires Dans la déclaration de procédure, pour faire
propre, on prend la précaution de dire que n est positif. Un nombre négatif
induira le message "invalid". Le calcul est basé sur la puissance de
l'instruction irem: elle calcule le reste
de la division de m par 10, lequel est ajouté à la somme s déjà calculée. Cette instruction produit également le quotient
en troisième paramètre ('m'), lequel devient la nouvelle valeur de m pour la
prochaine itération. |
|
|
Calcul direct (programmation
avancée)
Pour info
|
Commentaires add: addition des nombres qui suivent. op produit la suite des nombres à partit d'une
liste. convert n en base 10:
transforme n en une liste de chiffres. ^~2 est un "element-wise Operators" qui
est utilisé pour effectuer une opération sur tous les éléments qui précédent,
ici le carré.
|
|
Recherche des nombres Heureux
|
But Exploiter le programme de calcul direct pour
établit la liste des nombres heureux et les tristes Procédure Hx Élimination d'entrée des cas n = 1 ou 4. Calcul de la première somme, puis boucle pour la
suite tant que la somme n'est ni 1 ni 4. En sortie, évaluation binaire de s: true or false. Programme principal Instruction selectremove
qui trie les Hx true et les Hx false sur la suite des nombres de 1 à 20. |
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/CycleCar.htm |
![]()