NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/01/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Itérations
Débutants Nombres	Triangles de NOMBRES			Glossaire Nombres
INDEX Triangles Nombres	Des nombres	De Pascal	De Leibniz
		Sommaire de cette page >>> Approche >>> Le triangle des nombres >>> Explications >>> Carrés >>> Colonne centrale >>> Divisibilité par 3 >>> Produit – Démonstration

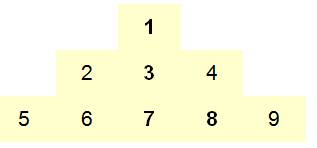
TRIANGLE des NOMBRES

En inscrivant les nombres entiers les uns après les autres dans ce triangle, un certain nombre de propriétés se révèlent. Que de surprises …

Approche
Il s'agit d'aligner les nombres successifs selon une sorte de pyramide. Chaque ligne comporte un nombre de plus, de chaque côté. A priori, rien de spectaculaire! Et pourtant …	Tiens! On constate la présence de carrés en bout de ligne.

Devinette

Dans une telle pyramide quel est le nombre immédiatement au-dessus de 2019 ?

Internet parle d'un habitant de l'appartement 2012 qui voudrait aller dire deux mots à son voisin du dessus qui fait du tapage.

Solution

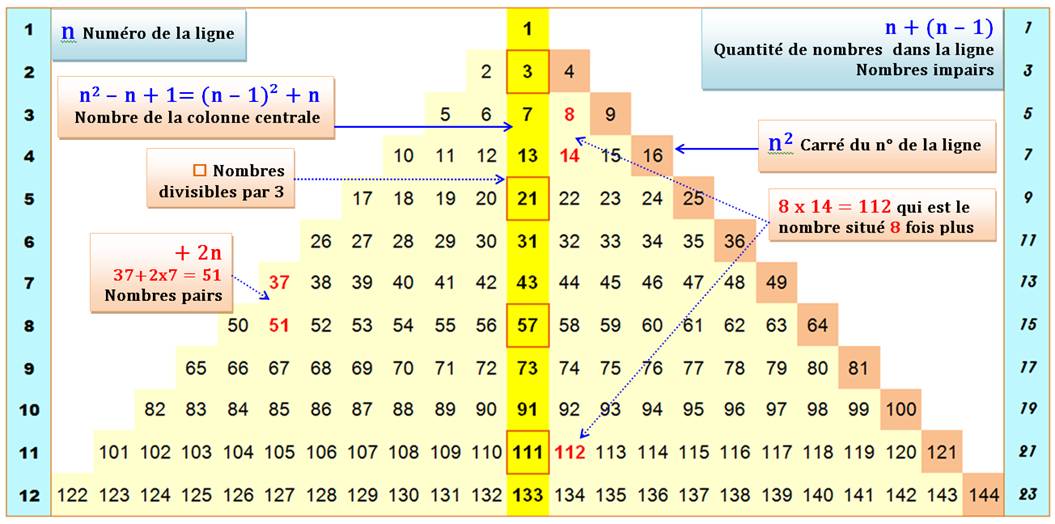
Le triangle des nombres jusqu'au douzième niveau

Explications
Numéro	La colonne de gauche indique le rang n des lignes successives.	n
Quantité	La colonne de droite indique la quantité de nombres dans la ligne. Ce sont les nombres impairs successifs.	n + (n – 1) = 2n – 1
Dessus- Dessous	Les écarts qui séparent les nombres entre deux lignes correspondent à la suite de tous les nombres pairs.	2n
Carré	Le bord droit du triangle fait apparaître tous les carrés successifs.	n^2
Centre	La colonne centrale est facilement calculable.	n^2 – n + 1
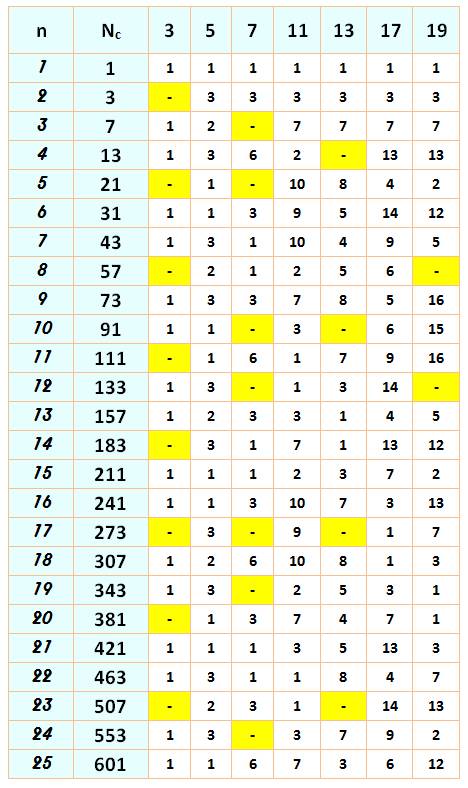
Division par 3	Un nombre sur quatre est divisible par 3 dans la colonne centrale.	3, 21, 57 …
Produit	Le produit de deux nombres l'un sous l'autre est dans la même colonne, k cellules plus bas, k étant le nombre le plus petit du produit.	8 x 14 = 112

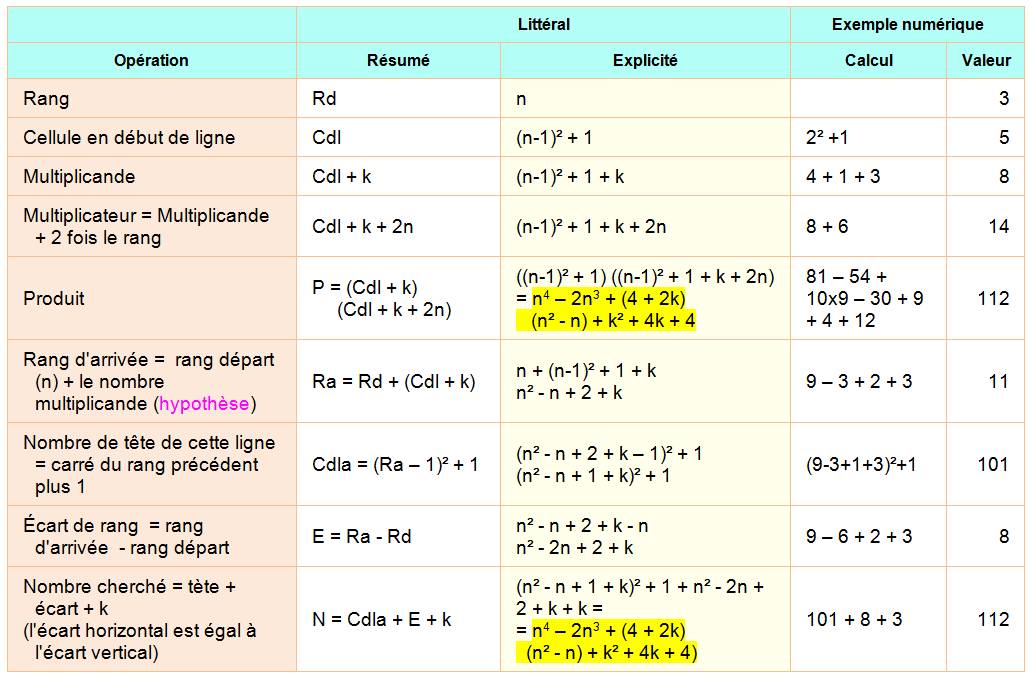
Ces propriétés sont explicitées ci-dessous

Carrés
Différence entre deux carrés: elle est égale à la quantité de nombres dans la ligne. pas étonnant de retrouver les carrés en bout de ligne.	n² – (n – 1)² = 2n – 1 = n + (n – 1) = quantité de nombres dans la ligne
Pour passer d'un carré au suivant, on lui ajoute la somme des deux nombres concernés

Colonne centrale
Les nombres de la colonne centrale se trouvent au carré précédent plus la moitié de la ligne (en respectant les quantités entières).	Nc = (n – 1)² + (2n – 1 + 1) /2 = n² – 2n + 1 + n = n² – n + 1

Divisibilité par 3
Point de départ: le nombre 3 en rang 2 et les suivants sont en rang 2 + 3k. Avec d'autres formules en n + mk, on trouve cette propriété pour les premiers suivants à raison de un sur deux. C'est ce que montre le tableau suivant.		N3 = n² – n + 1 avec n = 2 + 3k N3 = (2 + 3k)² – (2 + 3k) + 1 = 4 + 12k + 9k² – 2 – 3k + 1 = 9k² – 9k + 3 = 3 (3k² – 3k + 1) Divisible par 3
Nc est le nombre central de rang n. Les cases en jaunes montrent les cas où le nombre central est divisible par le nombre premier en tête de colonne. C'est le cas pour 3 7, 13, 19 … mais pas pour 5, 11 17 … Les nombres dans le tableau sont les valeurs des restes de la division (le modulo).

Produit - Démonstration

Un bon exercice d'algèbre qui exploite les propriétés du triangle des nombres. On procède en deux étapes: On calcule le produit littéralement, tout en vérifiant les valeurs numériques obtenues avec l'exemple 5 x 8. En faisant l'hypothèse que la propriété est vraie, le résultat est calculé littéralement, toujours avec la vérification numérique. En final, il s'agit bien de la même formule dans les deux cas (marquée en jaune). n est le numéro de la ligne et k est le rang dans la ligne (exemple numérique avec n = 3 et k = 3 qui désignent le nombre 5 dans le triangle des nombres)

Devinette – Solution

Dans une telle pyramide quel est le nombre immédiatement au-dessus de 2019 ?

Quel est le carré immédiatement supérieur: 45² = 2025 et 44² = 1936

De 2019 à 2025, il y a 6, soit 1936 (6 – 1) = 1931

Soit la disposition:

1931 1932 1933 1934 1935 1936

2019 2020 2021 2022 2023 2024 2025

Retour

Bilan

Un simple tableau de nombres nous apprend les nombres pairs, impairs, les carrés et leur progression, la divisibilité … et l(occasion d'un bon exercice d'algèbre.

Suite	Triangle de Pascal Spirale de Ulam
Voir	Barre magique des nombres premiers Boucle infernale Calcul mental Combinaisons Formule du binôme Géométrie – Index Petit théorème de Fermat Récurrence Théorie des nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgNombr.htm