|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SPIRALES des nombres PREMIERS Spirales d'Ulam En
enroulant les nombres premiers
sur une spirale, certains
alignements apparaissent. Signe d'un certain ordre dans les nombres premiers.
Ordre qui reste bien mystérieux, s'il existe! Il
est plus facile d'isoler des zones entières de
nombres composés. |
Anglais: Ulam Spiral, prime spiral
|
|
|
|
En
1963, le mathématicien Stanislaw Ulam
s'ennuie "grave" durant une conférence, il se met à dessiner une grille
et à y placer les nombres selon une spirale en plaçant le nombre 1 au centre. Il
y noircit les nombres premiers, et, surprise! Il découvre des alignements
obliques. Succès assuré. Sa spirale fit la une du magazine Scientific
American de mars; Martin Gardner y consacre un article: The Remarquable Lore
of the Prime Numbers. Exemple
du départ de la spirale d'Ulam et
allure pour 160 000 nombres
|
|
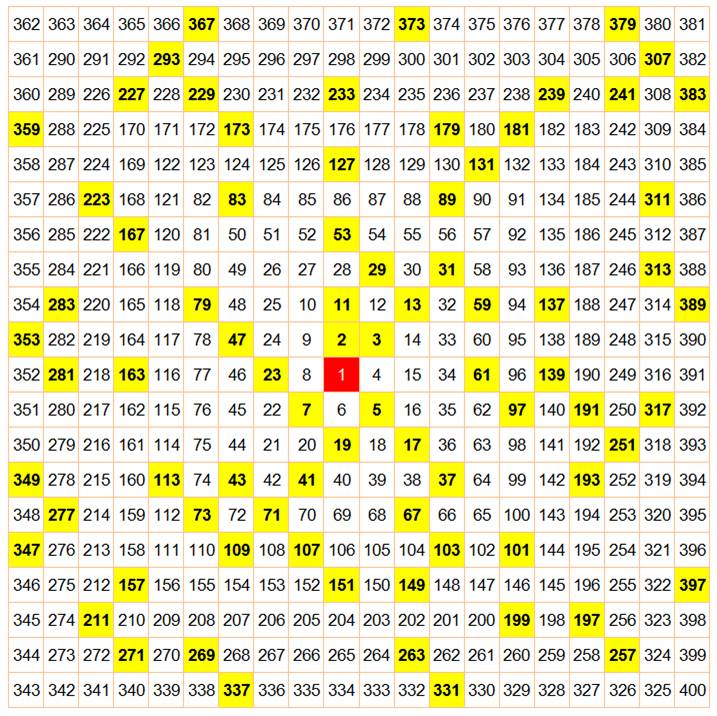
Exemple de 1 à 400
|
|
|
Notez que les carrés sont placés sur la diagonale
descendante, légèrement décalée à droite pour les carrés des nombres pairs. Un
carré apparaît à chaque demi-tour de la spirale. Voir Curiosités sur le spirale d'Uman
À gauche 160 000
nombres dont 14 683 sont premiers (en noir) En
poursuivant cette présentation pour une très grande quantité de nombres, on
remarque quantité d'alignements. Ces
alignements correspondent à des polynômes du 2e degré du type: y = a.x² + b.x + c Et,
voilà! C'est la naissance de la recherche de formules
qui produisent un maximum de nombres premiers. La
conjecture F de Hardy et Littlewood (1923) pourrait
expliquer quelques propriétés de cette spirale. Certains
affirment que la sprirale d'Ulam apporte peu d'information sur les nombres
premiers, à preuve, le même dessin avec des nombres aléatoires aurait à peu
près la même allure. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
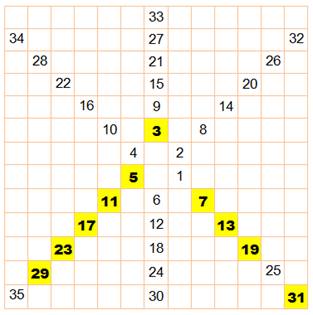
On
remarque que l'équation
y = 4 x²
+ 10 x + 5 représente
l'un des segments du tableau :
Les
cinq premières valeurs sont premières. En
tenant compte de ce type d'équations, on peut construire des spirales
appropriées (en choisissant le nombre central c).
Les deux plus célèbres sont les suivantes: x² + x +
17
x² + x +
41
Source: Experimenting
with the Ulam Spiral – Wolfram Cette formule en 41 produit de très nombreux nombres
premiers, comme le montre la diagonale montante de ces deux graphiques. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Équations des lignes de la spirale et comment les
établir
|
|
||
|
Spirale hexagonale
ou de Marteinson Les nombres sont enroulés
sur une spirale à six pas. Or comme les nombres premiers sont tous de la
forme 6k Voir tous ces graphes en cercles de 4, 6, 12, 24
/ Crible de la roue – Cercle à 30 rayons |
|
|
|
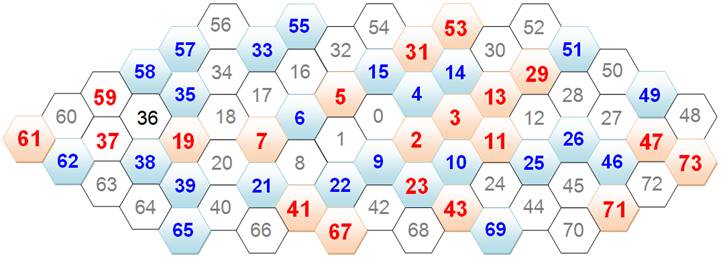
Spirale d'Abbott
(2005) Cette fois, les nombres
premiers sont disposés sur une spirale formée d'hexagones. Les adeptes de cette spirale y
marquent les nombres premiers et les nombres semi-premiers (nombres à deux facteurs
premiers) et tentent d'y repérer des alignements ou des blocs.
|
||
|
Spirale de Sacks
(1994) Les nombres premiers sont
placés sur une spirale d'Archimède en commençant par 0 (Illustration). Cette fois les carrés
apparaissent à chaque tour de la spirale. premier tour avec 2, 3 et 4; le
suivant avec 5, 6, 7, 8 et 9; etc. |
|
|
|
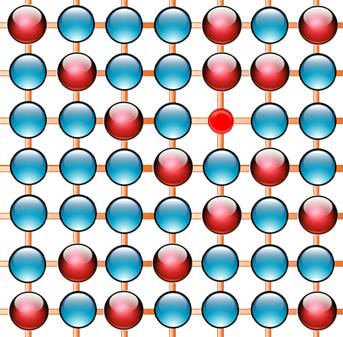
Spirale avec
quantité de diviseurs Chaque nombre est représenté
par un disque dont le diamètre est proportionnel à la quantité de diviseurs de ce
nombre. La quantité de diviseurs des
nombres premiers étant 2. |
Extrait de: Spirale d'Ulam –
Wikipédia |
|
|
Spirales de
séquences particulières Certains ont cherché à
appliquer cette méthode aux séquences classiques des nombres: Fibonacci, Lucas … vainement à ma connaissance ou
alors avec des conclusions très tirées par les cheveux. |
||
|
|
|||
|
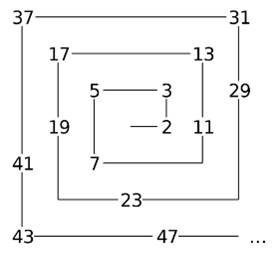
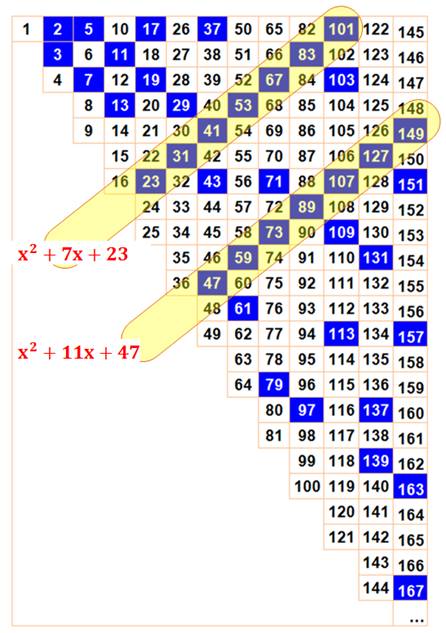
Vous vous
souvenez que la spirale d'Ulam montre un nombre carré à chaque demi-tour. Plaçons les nombres
successifs en colonnes, avec changement de colonne à chaque carré : 1, 4, 9,
16 … Là-aussi, repérons les
nombres premiers. Des alignements apparaissent. Prenons la diagonale en 23,
31, 41. La différence est la suite des nombres pairs: 8 , 10, 12 … La
différence seconde est égale à 2. Ces nombres peuvent être représentés par
une courbe du second degré. En l'occurrence: x² + 7x + 23. Nous découvrons ainsi de
nouveaux polynômes quadratiques qui engendrent des séquences de nombres
premiers. |
|
||
|
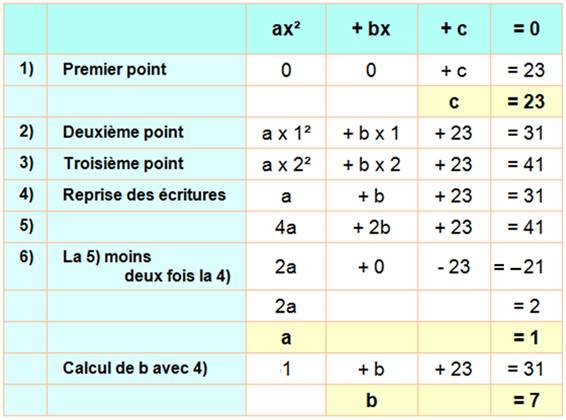
Établissement de l'équation On utilise les trois
premiers points (0, 23), (1, 31) et (2, 41) pour déterminer les trois
coefficients inconnus de ax² + bx + c. |
|
||
Cette présentation est une idée de Christophe L.
|
|
|
|
In 1963 Stanislav Ulam came up with a way to graph prime
numbers which seemed to indicate some recognizable structure in a graph of
the primes. People have since that time made elaborate graphs showing these
patterns, believing them to be of significance. Ulam marks the primes in the
spiral and studies the visual display for patterns or almost-patterns in the
primes number sequence. By use of a computer at Los Alamos, he is able to
generate displays having around 65,000 points in them. The Ulam spiral is a method of
visualizing the prime numbers that shows the apparent tendency of certain
quadratic polynomials to generate unusually large numbers of primes. It was
discovered by Stanisław Ułam in 1963 while doodling during the
presentation of a long and boring paper. He constructed the spiral by writing
down a regular rectangular grid of numbers, starting with 1 at the centre,
and spiraling out. Many decades earlier in 1923, Hardy
and Littlewood stated a conjecture that, if true, may explain many of the striking properties of the Ulam spiral. NB. The Ulam spiral, or prime spiral is also called the
Ulam Cloth
in other languages. Attention pas
clock, l'horloge; mais cloth le tissu, le chiffon en anglais. Quelle est la
signification dans les soi-disant autres langages? Est-ce parce qu'une
boutique américaine commercialise le dessin de la spirale d'Ulam sur des
tissus pour kilts? |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()