introduction à la programmation par l'exemple

Édition du: 13/01/2023

INDEX Logique Algorithme Programmation Multimédia	LOGIQUE et IA
	Introduction	Algorithmes	Jeux	Théorie
	Humaine	Machine de Turing	Systèmes experts	Rx neuronaux
	Programmation	Automate	Lambda-calcul	Robots
	Historique	Algorithmes TOP 15	ChatGPT	IA Avancée

PROGRAMMATION

Petit florilège en guise d'introduction.

Vous allez apprécier la simplicité du dessin du cercle en programmation fonctionnelle.

Vous verrez aussi des exemples de telles simplicités abstraites avec les nombres.

Sommaire de cette page

>>> Approche

>>> Dessiner un cercle – Classique

>>> Dessiner un cercle – Récursive

>>> Factorielle – Classique

>>> Factorielle – Récursive

Débutants

Logique

Glossaire

Logique

Approche

La programmation a beaucoup évolué au cours de ces décennies. À l'origine, il fallait connaître la structure interne du calculateur et, le programmeur avait trois tâches à gérer:

désigner des variables: codage du problème;

dérouler un algorithme: mécaniser la résolution du problème; et

organiser les manipulations de données: s'adapter aux possibilités de la machine.

Aujourd'hui, les inventeurs de langages, les spécialistes du génie logiciel, tentent de créer de plus en plus d'abstraction par rapport à ces tâches.

Les langages évolués s'affranchissent des contraintes dues aux ressources matérielles;

Les langages fonctionnels font disparaître les variables.

De leur côté, les systèmes expert et les réseaux de neurones sont un moyen de confier la constitution de l'algorithme au système.

Voir Trois méthodes de programmation

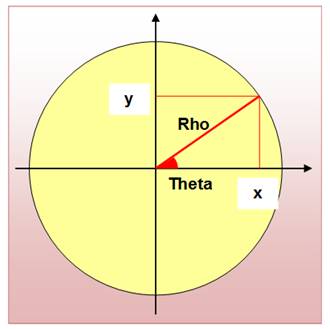
DESSINER un CERCLE – Méthode classique
	PROGRAMME # On déclare et on initialise les variables Rho := 12; Theta := 0; x := 0; y := 0; # On réalise une boucle sur 360° # À chaque pas défini en degré par la valeur de i, on calcule x et y en fonction du rayon (Rho) et de l'angle (Theta) pour i de 0 à 359 faire Theta := i; *x := Rho cos(Theta); y := Rho * sin(Theta); dessiner le point (x, y); fin;**
Explications	Langage du type Maple
#	Le texte sur cette ligne est un commentaire.
;	Indique la fin d'une instruction.
Rho := 12	On attribue la valeur 12 à la variable Rho.
pour i de 0 à 359	Le programma va calculer toute la séquence d'instructions jusqu'à fin avec les valeurs successives i = 1, puis i = 2 … jusqu'à i = 359.
Theta := i	On attribue la valeur de i (d'abord 1, puis 2 …) à la variable Theta. Theta prendra successivement toutes les valeurs d'angle de 0 à 359 degrés.
*x := Rho cos(Theta);**	Calcul de x = Rho . cos(Theta).
*	Veut dire multiplier. Astérisque pour ne pas confondre x (multiplier) et x (inconnue).
dessiner le point (x, y);	Allume le pixel de coordonnées x et y sur l'écran.
fin;	Marque la fin de l'instruction faire.

Voir Trigonométrie / Cercle

DESSINER un CERCLE – Méthode récursive
	PROGRAMME Pour CERCLE faire Si ARRIVÉE = DÉPART alors ARRÊT AVANCER d'un pas en avant TOURNER d'un cran à gauche CERCLE FIN
Explications	Langage du type Logo
Pour CERCLE	Définition d'une procédure. Chaque fois que CERCLE est appelé, on exécute le programme.
AVANCER d'un pas	On avance d'un pas devant soi; le pas étant défini au préalable. Cette progression a été comparée à celle d'une TORTUE dans le langage LOGO. Notez qu'il ne s'agit pas d'un positionnement absolu (en x et y), mais en relatif (par rapport à là où je suis et selon la direction devant moi).
TOURNER d'un cran	Original comme instruction! La "tortue" pivote d'un cran, la valeur du cran étant définie quelque part.
Avant, arrière, à gauche, à droite	Ce sont les quatre instructions pour commander la "tortue".
CERCLE	On rappelle la procédure cercle. Elle va régénérer un pas en avant et une rotation d'un cran. Oui, c'est curieux de faire appel à soi-même. C'est ce qui est nommé une procédure récursive.
Arrêt	Tel quel, la tortue parcourt le cercle sans fin. Un critère du type, je suis déjà passé là, permettra de déclencher l'arrêt de la tortue.

Voir Cercle pas à pas / Cercle avec Scratch / Les quatre tortues / Programmer en jouant avec Scratch

FACTORIELLE – Méthode classique
PROGRAMME	Déroulement	Variables	Résultats
F := 1; Pour i de 1 à 10 faire F := F * i ; imprimer (i, "! =", F) ; Fin Langage du type Maple	On débute avec	F = 1
	La première boucle avec i = 1 donne	F = F_ancient . i F = 1 x 1 = 1
	On imprime		1! = 1
	La deuxième boucle avec i = 2 donne	F = F_ancient . i F = 1 x 2 = 2
	On imprime		1! = 2
	La 3^e boucle avec i = 2 donne	F = F_ancient . i F = 2 x 3 = 6
	On imprime		3! = 6
	Etc. jusqu'à i = 10.

Voir Factorielle

FACTORIELLE – Méthode récursive 1
PROGRAMME	Commentaires
int fact (int n) { if (n = = 0) return 1; *return n fact (n – 1);** }	Typiquement récursif, car la procédure s'appelle elle-même. Langage du type C.
Si n vaut 0, c'est fini.	Le programme retourne un entier (integer, abrégé en int) qui vaut 0.
Si n vaut 3, par exemple	Le programme veut retourner 2! qu'il ne connaît pas encore. Il réinjecte 2 dans le programme et cherche 1! qu'il ne connait pas. Ainsi de suite, jusqu'à arriver à 0 qu'il connaît. Il remonte ensuite toute la chaîne: 0! = 1 1! = 1 2! = 2 3! = 6

FACTORIELLE – Méthode récursive 2
PROGRAMME	Commentaires
FAIRE fact n = SI n = 0 ALORS 1 *SINON n fact (n-1);;**	Encore plus simple à écrire. Basé sur le même principe récursif que ci-dessus On arrive à une telle concision C'est une écriture fonctionnelle
Code exact # let rec fact n = if n=0 then 1 else n*fact (n-1);;	Langage du type OCaml Langage diffusé par l'INRIA

Pourquoi développer des capacités informatiques chez les enfants.

La pratique de l’informatique, à l'aide d'objets ludiques comme les logiciels du type Scratch ou même des jouets du type robots, développe trois grandes qualités:

Capacité à résoudre des problèmes: les enfants sont devant des briques logiques, des capteurs, des moteurs et ils doivent résoudre un problème par eux-mêmes, penser par eux même pour arriver au résultat.

Pensée critique: un programme ne marche jamais du premier coup. L’enfant doit critiquer son propre raisonnement et chercher à résoudre les anomalies. C’est d’autant plus utile que l’école française développe peu cette capacité.

Pensée créative: un problème simple ou complexe peut être résolu de plusieurs façons différentes en informatique. Les enfants développent leur capacité à passer à travers les difficultés, chacun à sa manière.

Suite	Automate Algorithmes – Index Programmation – Index HTML Informatique
Voir	Crible d'Ératosthène Dualité Énigmes et paradoxes Factorielle Fractales Fractales en programmation Incomplétude Intelligence Logique – Index Multimédia et informatique – Index Outils de la logique Puissance de calcul Raisonnement Réseaux neuronaux Systèmes experts
Sites	Programmer en jouant avec Scratch (Jouer en ligne ou télécharger gratuitement le programme- Amusement immédiat!).
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Logique/IAProgra.htm