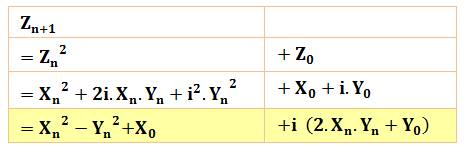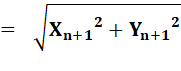|
|||||||||||||||||||||||||||||
![]()
|
FRACTALES en PRATIQUE Comment construire soi-même des
dessins fractals et approcher ces objets si fascinants. Comme pour un moteur ou une montre, vous
allez avoir l'occasion d'aller voir comment c'est fait. Quatre étapes relativement faciles:
|


|
|
|
|
Plusieurs possibilités selon votre passion pour
les fractales Contemplatif Consulter tout simplement les nombreux sites Internet pour de jolies images fractales, avec
n'importe quel moteur de recherche. Interactif Se procurer le shareware FRACINT qui permet de construire
toutes sortes de fractales en jouant sur les paramètres de définition (se télécharge sur
Internet). Il en existe d'autres que vous trouverez sur Internet sous le
nom: fractal generator on line Actif Faire le programme avec votre logiciel
préféré, ça vaut vraiment l'effort. Sous vos yeux vous apprécierez l'aspect
magique de ces êtres mathématiques. Autant de
"complexité esthétique" avec une formule si simple ! Expert Vous pouvez approfondir la théorie concernant
les fractales de tout type, et voir comment construire de belles images dans
le livre célèbre: " the science of fractal images de Barnsley, Devaney,
Mandelbrot, Peitgen, Saupe, Voss - Éditions Springer Verlag. |
|
Voir Réflexion sur
les Fractales
![]()
Construction: théorie et programmation
|
|
||
|
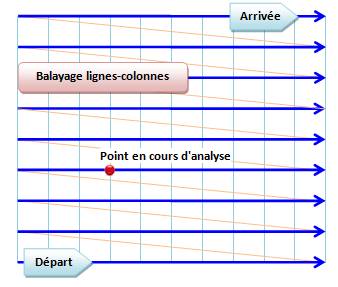
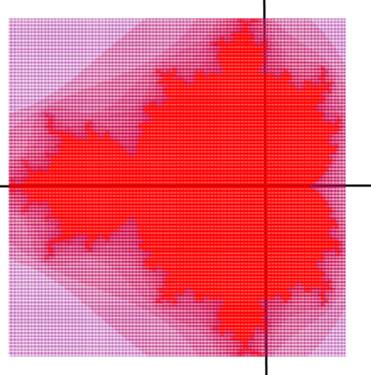
Imaginez
un balayage du plan en lignes et colonnes. Tous les points sont
méthodiquement passés en revue. Chacun de
ces points est analysé pour décider quelle couleur lui associer. |
Balayage en x et y et analyse de chaque
point |
|
|
Le
traitement appliqué est particulièrement simple: il consiste à essayer de
déloger ce point. Alors, de deux choses l'une:
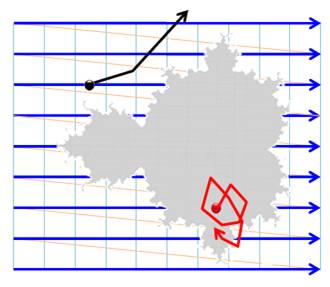
Après
analyse de tous les points, la forme fractale se dessine. |
Le point s'échappe: couleur blanche. Le point virevolte localement: couleur
noire. |
|
|
|
|||
|
Vous
connaissez le célèbre cycle de
Syracuse: un traitement est appliqué à un nombre, puis au résultat
trouvé, puis au résultat, etc. Il s'agit
d'une formule de récurrence
qui indique comment le nombre suivant
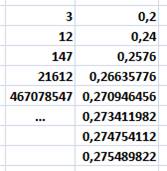
est obtenu à partir du nombre précédent. En utilisant le formule indiquée à droite et avec le nombre 3 comme
racine, il devient 3x3 + 3 = 12, puis 12x12 + 3 = 147, etc. Les nombres
suivants sont de plus en plus grands. Avec le nombre 0,2 les nombres suivants se cantonnent autour de 0,27. |
Formule de récurrence pour les fractales
Exemples ce calcul
|
||
|
Pour le
dessin de la fractale, nous n'allons pas utiliser un seul nombre. Nous allons
prendre les deux nombres qui caractérisent le point: son abscisse et son
ordonnée (X et Y). Une
technique de manipulation des points du plan consiste à associer les deux
coordonnées pour former un nombre complexe.
Inutile de connaitre ce domaine pour
suivre la suite. |
Coordonnées d'un point et nombres complexes Les coordonnées x et y sont associées en un nombre composé dit
complexe. On les sépare bien en multipliant le second par i, symbole des
nombres imaginaires. Z = X +
i.Y Le représentant de Z dans le plan est le point de coordonnées X et Y. |
||
|
Reprenons
la formule de récurrence, mais avec ces nombres complexes; et développons en
X et Y. Pour
tester si le point est papillon ou déserteur, on calcule le module du nombre
complexe. Le test consiste à exécuter un certain nombre d'itérations (15 par
exemple):
|
Formule de récurrence
Notes: on se souvient que i² = -1 La partie sans "i" est la partie réelle, et celle avec "i" en facteur est la partie imaginaire.
|
||
|
|
||
|
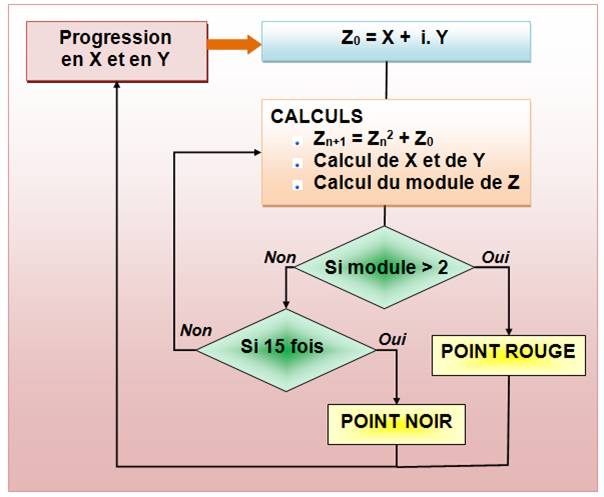
Un système de progression (balayage) en X et en Y est mis en place. Pour chaque couple (X et Y), calcul du point-racine (Z0)
puis entrée dans la boucle d'itérations avec à chaque fois le calcul du
module. Si le module s'envole, on pose un point rouge en X et Y. Sinon,
lorsque 15 itérations sont exécutées, on pose un point noir. |
|
|
|
|
||
|
|
Commentaires Le programme Maple commence par
réinitialiser tout (restart). Annonce d'une liste (L). Mise en route de deux boucles en i et j et calcul
des coordonnées x et y dans l'espace x (-1.5 à 0,5) et y (-1 à +1), zone
propice à la formation de la figure fractale. Calcul de z et z0. Mise en place de la boucle de 15 itérations et
calcul direct de la formule d'itérations. En effet, Maple sait faire les
calculs en nombres complexes: Re est la partie réelle (ou x) et Im est la
partie imaginaire (ou y). Si le carré du module (r) est supérieur à 4,
arrêt des itérations en forçant k à 15. Si le r reste inférieur à 4 jusqu'à la fin des
itérations, ajoutez le couple (x,y) à la liste L, témoignant que ce point est
interne au POU. Fin des trois boucles (od). Appel des programmes exécutant les tracés
(plots). L'instruction pointplot dessine les points aux emplacements désignés
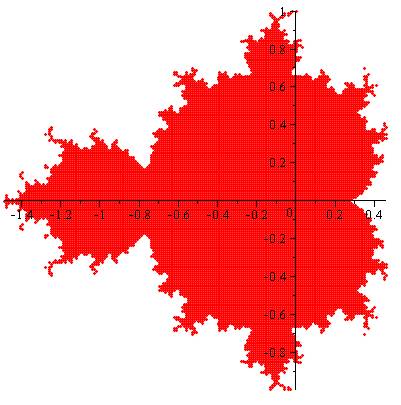
par les couples (x, y) présents dans la liste L. Résultat de l'exécution du programme qui dure
environ une minute. Il est possible de choisir d'autres paramètres.
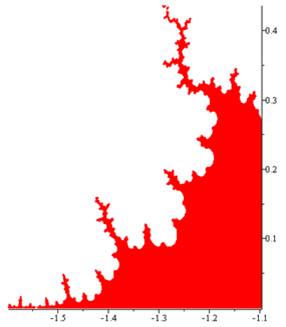
Exemple avec la zone extrême gauche (ci-dessous):
|
|
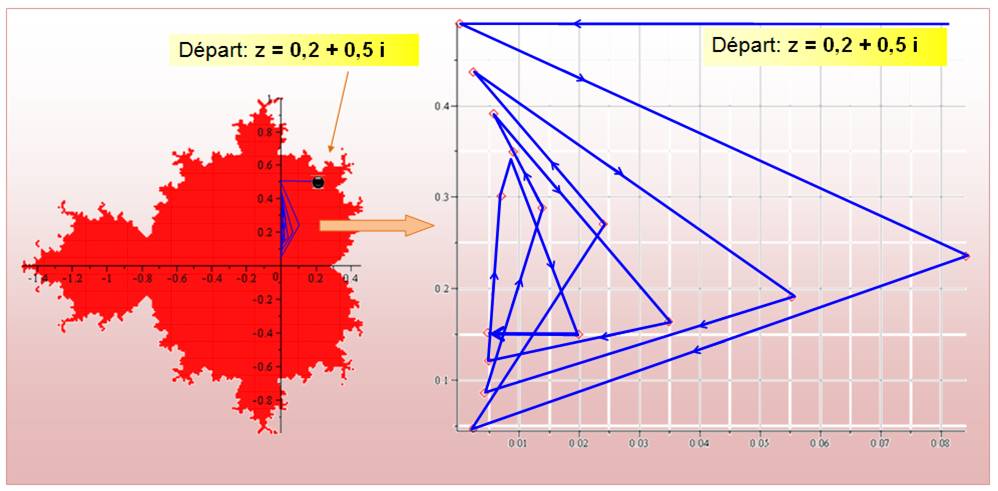
Exemple
de "papillonnage" pour le point (x = 0,2 et y = 0,5) pour 15
itérations
|
|
||
|
Le logiciel Scratch est téléchargeable
gratuitement et
immédiatement utilisable.
|
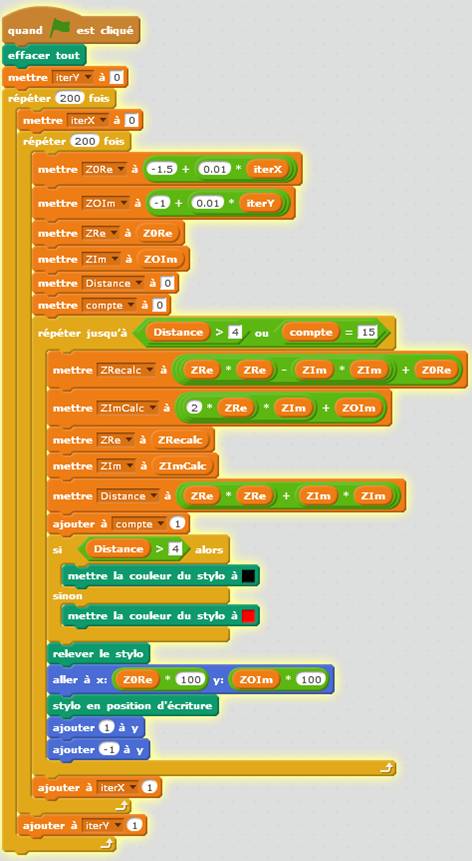
Commentaires Même avec le logiciel didactique Scratch, on obtient de bons
résultats. Démarrage en cliquant sur le drapeau vert.
Effacer tout sur l'écran. Boucles en Y et en X avec iterY et iterX. On met
ces paramètres à 0 au départ et on incrémente en fin de boucle. Z0Re est la partie réelle de Z0 (soit x) qui
commence à -1,5 et progresse 200 fois de 0,01 jusqu'à 0,5. Idem pour Z0Im, la
partie imaginaire (soit y). Initialisation de ZRe (partie réelle de Z) et de
ZIm (partie imaginaire). Distance (module) est mis à 0 pour permettre de
passer le premier test. La variable "compte" va comptabiliser
la quantité d'itérations. Boucle d'itération sur le point (X,Y). Arrêt si
distance supérieure à 4 ou si 15 itérations ont été effectuées. Calcul des parties réelles et imaginaires de Z,
mises temporairement dans ZRecalc et ZImcalc. Calcul de la distance et passage à l'itération
suivante en incrémentant la valeur dans compte. Selon la distance trouvée, mise en place d'un
stylo noir ou rouge. Mettre le stylo en bonne position (x, y) sur
l'écran (100 fois les valeurs Z0Re et Z0Im). Stylo baissé, faire un petit trait (y + 1 et y –
1). Incrémenter les pointeurs iterX et iterY en fin
de leur boucle respective. Le résultat de l'exécution de ce programme est montré
ci-dessous. Durée: environ deux heures. |
|
|
Autre exemple de sortie en supprimant le petit trait en y
|
||
Voir Ensemble de Mandelbrot en
Processing / Programmation de la
fractale du nombre Fibonacci
|
Dans le cadre des loisirs, nous étions très nombreux dans
les années 1980 à découvrir à la fois:
Pour mon compte, je n'ai pas gardé trace de ces images et
encore moins des programmes qui ont disparus avec l'obsolescence de ces
ordinateurs de l'époque. 1 Comme
beaucoup de personnes de ma génération dans le début des années 1970, j'avais
essentiellement codé en assembleur, Algol et Fortran dans le cadre scolaire
et professionnel. |
Voir Informatique et programmation
Très profond dans l'ensemble de Mandelbrot

Source
image: Dimensions – Jos Leys 6/9
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()
![]()
Archives
|
|
||||||||||||||
|
Voir Algorithmes Balayage
du plan en X et en Y
–2,4 < X < 2,4 –1,5 < Y < 1,5 avec une profondeur d'itération de 16
(Quantité de calculs de la formule pour déterminer si le résultat tend vers
l'infini ou se stabilise sur une valeur fixe.
Boucle
de test de la convergence
Z0 =
0 ZN+1 = ZN²
+ C
Calcul
de ZN+1
|
||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
Les instructions sont simples et sont donc
très facilement adaptables au langage de programmation que vous possédez. Le petit effort en vaut la peine. C'est purement magique.
|
|||||||||||||||||||||||||||||
Zone des liens >>>
![]()