|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Crible d'Ératosthène Programmation
|
Anglais:
The Sieve of Eratosthenes
|
Liminaire – Pour
déterminer si p est premier |
|
|
du type "premier(p)" ou
"isprime(p)" … selon
le logiciel considéré.
l'un des nombres de 2 à p.
jusqu'à la racine de p. |
|
|
|
||
|
|
Ces nombres
successifs qui restent sont des nombres premiers. |
|
|
Élimination
des nombres pairs |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Élimination
des nombres divisibles par 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Élimination
des nombres divisibles par 5 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ensuite,
avec 7
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Méthode de la barre magique
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple
avec n = 100:
Conclusion: pour rechercher la racine de 100, on peut
se contenter de n'explorer que jusqu'à 10, nombre qui est la racine de 100. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Puissance du crible
|
Il suffit de huit étapes de filtrage pour
isoler les nombres premiers jusqu'à 400. Il en faut 168 pour aller jusqu'à un
million. C'est là toute la puissance du crible d'Ératosthène. |
With eight filtering steps, one can isolate the
primes up to 400. With 168 filtering steps, one can isolate the primes up to
1 million. That’s the
power of the sieve of Eratosthenes. |
|
Au
début des années 1700, on connaissait tous les premiers jusqu'à 100 000 grâce
à un mathématicien amoureux des nombres: John Pell. Vers
1800, on les connaissait jusqu'à un million. Vers 1850, Jacok Kulik eut l'ambition d'aller jusqu'à
100 millions. Un certain Hildenburg utilisait des réglettes pour simuler le
crible; d'autres des pochoirs. |
|
Voir Historique
|
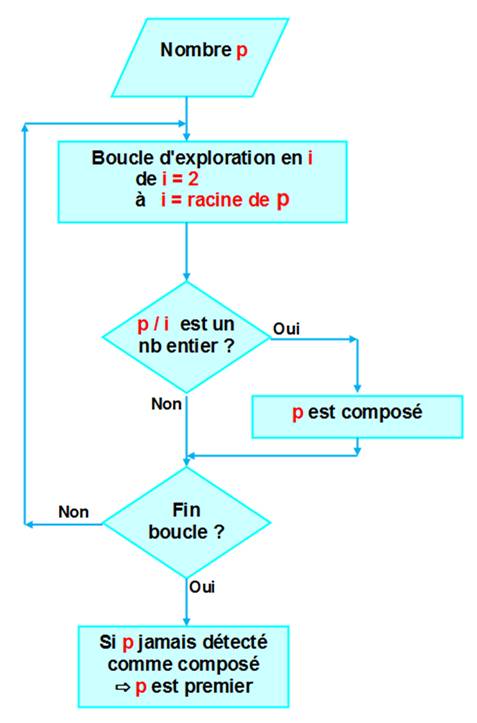
ALGORITHME - Phasage |
|
|
|
|
|
|
|
|
Pour un nombre p, candidat pour être
premier, nous explorons toutes les valeurs d'un nombre i depuis 2 jusqu'à
racine de p. Pour chaque valeur de i nous cherchons s'il
est un diviseur de p. Si oui, c'est que
le nombre est composé. Nous mémorisons ce fait et
nous poursuivons (bêtement) l'exploration pour ne pas compliquer l'algorithme
(pour le moment). Le nombre est décrété premier si aucun
diviseur n'a été trouvé.
|
|
Voir Algorithme
|
Programme |
Commentaires |
||||
|
On se donne p |
Donnée d'entrée dans ce programme de
test de primalité de p. |
||||
|
|
|
|
|
|
Initialisation de la boucle de test. |
|
|
imax := racine de p |
Valeur maximale pour le crible. |
|||
|
|
premier:=1 |
|
|
On fait l'hypothèse que p est premier. premier est un
indicateur à 1 si p est premier et 0 sinon.
On place cet indicateur dans
cette position par défaut et on va observer s'il résiste dans cette position. Note: le nombre
1 n'est pas premier >>> |
|
|
|
|
|
|
|
Lancement de la boucle de test. |
|
|
Boucle pour i à partir de 2 jusqu'à imax |
Il s'agit d'une boucle d'itérations. Le programme effectue le parcours de
la boucle pour toutes les valeurs de i. |
|||
|
|
|
Division de p par i |
Division par toutes les valeurs
successives que prend i. |
||
|
|
|
Quotient entier ? |
Si le quotient est entier, c'est que
p est divisible par i. |
||
|
|
|
|
Oui |
premier :=0 |
p est divisible par i, p est
composé, p n'est pas premier. |
|
|
|
|
Non |
aucune action |
On conserve l'indicateur premier
dans son état. |
|
|
Fin de la boucle |
L'exploration pour chacun des
nombres de 2 à i max est finie. |
|||
|
|
|
|
|
Fin de la boucle de test. |
|
|
premier à 1 si p est premier premier à 0 si p est composé |
On observe l'indicateur
"premier" Dans la suite du programme, il suffit de tester la valeur de
l'indicateur pour savoir si p est premier ou non. |
||||
|
Une première
amélioration consiste à stopper l'exploration dès que le nombre est détecté
comme composé. Facile, il suffit de forcer i à prendre tout de suite la
valeur de la racine de n.
On peut encore
limiter le nombre des recherches en explorant uniquement les nombres en 6n plus ou moins un, car tous les nombre premiers
sont de cette forme. |
|||||
Voir
Programmation
|
|
||
|
p:=109:
imax:=round(sqrt(p)): premier:=1:
for i from 2 to imax do div:=
evalf(p/i): if
frac(div)=0 then
premier:=0:
fi: od: if
premier=1 then lprint(p,
est_premier): fi: |
On prend p = 109 comme exemple. Sa racine arrondie est placée en
imax, qui doit être un nombre entier. On positionne l'indicateur premier
à 2. On lance la boucle d'exploration.
Dont l'anglais se lit en français: "pour i de 2 à imax faire"
Le résultat de la division évalué en
décimal est placé en div. Si la partie décimale est nulle, le
nombre est entier. Et, p est divisible par un i;
l'indicateur premier est mis à 0. Fin du test de divisibilité. Fin de la boucle d'exploration en i. Si l'indicateur premier
est à 1, le nombre est premier. L'imprimer. Fin. |
|
|
109
est_premier |
<=
Exécution du programme. |
|
Le
programme tel qu'il apparait dans le logiciel Maple

Programmation du type Maple (marque Waterloo Maple, logiciel mathématique)
Voir Programme
Python / Autres
cribles
|
Premiers
d'Euler en n² + n + 41 |
|
|
|
k:=0: for n from 1
to 107 do p:= n*n + n + 41: |
On initialise un compteur k pour
comptabiliser la quantité de premiers trouvés. Boucle sur la plage de recherche. Ici;: tous les nombres n de 1 à 107 Calcul du nombre p à partir de la
valeur de n. |
|
|
imax:=round(sqrt(p)): premier:=1:
for i from
2 to imax do div:=
evalf(p/i): if
frac(div)=0 then
premier:=0:
fi: od: if
premier=1 then lprint(k, n, p): fi: |
Programme de recherche si p est
premier C'est exactement celui vu ci-dessus. Lors de l'impression si p est
premier, on donne aussi la valeur de n
correspondante et la quantité de
premiers déjà trouvé. |
|
|
od: lprint ( evalf ( 100*k / (n-1) ) ) ; |
Fin de la boucle d'exploration en n. On imprime le pourcentage de nombres premiers trouvés par rapport à la quantité de nombres
explorée. |
|
|
Résultat de l'exécution |
|
||||||||||||||
|
On trouve
successivement k, numéro; n, la variable; et, p
le nombre premier d'Euler associé à n.
Sur cette plage
pour n jusqu'à 107, la proportion de nombres premiers d'Euler est de 85%. |
|||||||||||||||
|
La
recherche des nombres premier en utilisant le crible d'Ératosthène est vite limité du fait de sa gourmandise
en place mémoire. En
2016, Harald Helfgott développe un algorithme qui réduit le besoin de place
par 100 ou plus. C'est lui qui, en 2013, a démontré la conjecture faible
de Goldbach (tout nombre plus grand que 5 est la somme de trois nombres
premiers). Mais
Helfgott s’est inspiré
d’une technique de calcul analytique appelé la méthode du cercle pour que le
crible d’Ératosthène fonctionne avec peu de mémoire. En termes mathématiques,
plutôt que d’utiliser un espace N, le crible utilise la racine cubique de N.
Selon Helfgott, pour calculer tous les nombres premiers jusqu’au trillion, la
version modifiée du crible nécessite quelques millions de bits au lieu de
milliards de bits. Source: New Take on an Ancient Method Improves Way
to Find Prime Numbers The modified
version of the sieve of Eratosthenes could accelerate computer calculations –
Scientific American et sa tradition
en: Mathématiques – Le
Crible d’Ératosthène pour optimiser la recherche des nombres premiers –
Jacqueline Charpentier – 28/09/2016
(Actualité Houssenia Writnig). |
![]()
|
|
||
|
|
Crible brut sans optimisation (comme exercice de programmation). Commentaires Le module time est importé pour mesure le temps
d'exécution du programme. Définition d'une fonction Crible d'Ératosthène. On place 2 comme premier nombre premier dans la
liste Premiers, et on commence
l'exploration à p = 3. E (comme éliminés) est une liste qui contient n
fois la variable booléenne False. Un False devient True
lorsque le nombre correspondant à sa position est éliminé. La variable p explore les nombres impairs; sa
valeur sera incrémentée de 2 (p += 2) en fin de boucle. Mais, tant que sa valeur est inférieure à n et
qu'il n'est pas en face d'un True , on
retient cette valeur comme nombre premier; il est ajouté à la liste Premiers et ses multiples ( i + p) sont positionnés en True dans la liste des éliminés. On note la durée d'exécution en fin de travail,
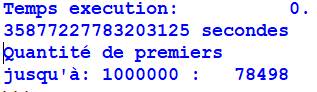
avant de retourner la liste finale des premiers Le programme principal appelle cette fonction
pour n = un million et indique qu'il y a 78 498 nombres premiers. Le temps 'exécution est d'environ un tiers de
seconde (0,358 …) Pour un milliard: |
|
Voir Programmation Python – Index / Programmation – Index
![]()
|
Voir |
|
|
Aussi |
|
|
|
|
|
Programmation |
|
|
Cette page |
![]()