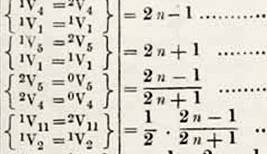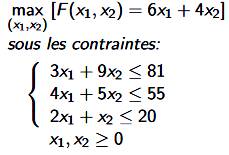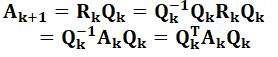|
Édition du: 13/01/2023 |
|
INDEX |
LOGIQUE et IA |
|||
![]()
|
ALGORITHMES – TOP 15 Les plus importants de l'histoire Algorithme, procédure, recette … sorte de
mode d'emploi très précis qui permet de produire un résultat attendu à chaque
fois qu'il est utilisé, même si les données de départ sont différentes. Un algorithme permet de résoudre un
problème répétitif, récurrent. C'est une suite d'opérations très précises
(instructions) qui permet de résoudre un problème ou d'obtenir un résultat. Quels sont les algorithmes les plus
importants qui ont marqué l'histoire? Ou, du moins, les grandes avancées en
procédures informatiques. Classement selon Christopher McFadden – 2018 Anglais: Algorithms can be found in many fields of science such as physics,
math, and computing. They have a long history with some being more
influential than others. On
rencontre les algorithmes dans de nombreux domaines des sciences comme la
physique, les maths et l'informatique. Avec une longue histoire, certains
furent plus déterminants que d'autres. Voir Anglais – Le bagage minimum
|
|||
|
|
Sommaire de cette page >>>
Algorithmes Babyloniens >>>
Algorithme d'Euclide >>>
Crible d'Ératosthène >>>
Algèbre de Boole >>>
Programmation avec Ada Lovelace >>>
Transformée de Fourier rapide >>>
Algorithme de classement de Google |
>>>
Méthode Monte Carlo >>>
Algorithme de SIMPLEX >>>
Méthode de résolution des espaces de Krylov >>>
Filtre de Kalman >>>
Algorithme QR >>> Compilateur
Fortran optimisé >>>
Algorithme de tri QUICKSORT >>>
Algorithmes de compression |
Débutants Glossaire |
Voir Les trois
algorithmes les plus célèbres aujourd'hui
|
|
||
|
Sans
doute les algorithmes les plus vieux du monde, découverts inscrits sur des tablettes
d'argile. Ces
algorithmes indiquent comment effectuer les opérations courantes tout en utilisant leur système de
numération particulier: sexagésimal
flottant. Ils
montrent également comment résoudre de nombreux cas d'équations algébriques en procédant
pas à pas par une suite précise d'instructions. Knuth
explique: les Babyloniens
fonctionnaient avec un "langage machine" et non un "langage
symbolique" comme le nôtre aujourd'hui. |
C'est Donald E. Knuth (mathématicien et
informaticien à l'Université de Stanford) qui publie en 1972 les premières
traductions de ces tablettes et met en évidence l'aspect algorithmique des
calculs.
|
|
|
|
||
|
L’un des
premiers algorithmes en théorie
des nombres qui n'ai jamais été créés, l’algorithme
d’Euclide s’utilise encore jusqu’à aujourd’hui. Il permet
de trouver les plus grands diviseurs communs de deux nombres ou entiers
positifs (PGCD). |
Euclide (v-325
à -275) est un mathématicien grec, père de la géométrie, auteur du manuscrit Les éléments dans lequel figure cet
algorithme. Algorithme d'Euclide: suite de
divisions itératives dont les résultats sont réinjectés dans la division
suivante. |
|
|
|
||
|
Le crible
d’Ératosthène permet de trouver tous les nombres
premiers à partir de 1 jusqu'au nombre que vous voulez. Toujours
efficace pour de petits nombres, il est supplanté aujourd'hui par d'autres
méthodes plus
sophistiquées. |
Ératosthène
(-276 à -194), connu pour avoir calculé la longueur du méridien
terrestre. Crible d'Ératosthène: écrire la
suite des nombres à partir de 2 et supprimez tous les multiples de 2. Le
nombre 3 reste en tête: supprimez tous ses multiples. Le nombre 5 reste en
tête: supprimez tous ses multiples. Etc. Les nombres de tête: 2, 3, 5 … sont premiers. |
|
|
|
||
|
L’algèbre
de Boole est la base de la conception de toutes les logiques
modernes que ce soit pour les circuits des ordinateurs (matériel- harware) ou
pour l'informatique (logiciel- software)
Il n'y
aurait pas d’ordinateurs ou de systèmes informatiques sans la
découverte de la logique booléenne. |
George Boole (1815-1864)
est un logicien, mathématicien et philosophe britannique. Algèbre de Boole: calcul logique à partir de 0 et de 1 (ou vrai,
faux; ou encore, le courant passe ou non; la mémoire est excitée ou pas;
etc.). La fonction
ET, par exemple, produit un "vrai" en sortie, seulement si les
toutes les entrées sont "vraies". Codé en binaire,
cela donne: 1 ET 1 = 1, mais 0 ET 1 = 0. |
|
|
|
||
|
L’algorithme
développé par Ada Lovelace est reconnu comme étant le premier programme
informatique destiné à être implémenté sur une machine. En 1953,
on a découvert un code informatique écrit par elle, permettant le calcul des nombres
de Bernoulli. Ce
programme est considéré aujourd’hui comme étant le premier exemple de code
informatique enregistré. |
Ada Lovelace
(1815-1852), mathématicienne britannique, fille de lord Byron le poète. En
duo avec Babbage
qui conçoit une machine à
calculer, elle en écrit le programme. Extrait du programme d'Ada Lovelace
|
|
|
|
||
|
Algorithme qui
transforme un signal temporel (qui est fonction du temps) en données
fréquentielles (son spectre de fréquences). Principe: on
part du constat que tout signal, même complexe, peut être reconstitué par sommation
de signaux plus simples à fréquences pures. Son emploi
révolutionna le domaine du traitement du signal. L'algorithme y est connu
sous le nom de FFT (Fast
Fourier Transform). |
Joseph Fourier
(1768-1830) est un mathématicien et physicien français surtout connu pour sa
théorie analytique de la chaleur. En fait c'est Carl Gauss en 1802 qui
initie ce type de procédé pour calculer l'orbite des astéroïdes. En 1822, Joseph Fourier élabore la théorie. La
version moderne, utilisée en traitement du signal, date de 1965, et elle est
due à James Cooley et John Tukey.
|
|
|
|
||
|
Le PageRank est sans aucun doute l’algorithme le
plus utilisé dans le monde. C'est lui
que vous sollicitez lorsque vous introduisez des mots dans le moteur de
recherche Google. L'importance
accordée à une page donnée est fonction de ses liens à d'autres pages, dans
les deux sens. |
Algorithme crée par Larry Page avec la contribution de
Sergey Brin, tous deux étudiants à l'université de Standford. Notez
qu'astucieusement l'algorithme porte le nom de son auteur principal: Page
rank (to rank veut dire: classer, hiérarchiser).
|
|
Voir GAFAM
|
|
||
|
La
méthode Monte-Carlo
est assez déroutante: elle consiste à approcher la solution à un problème par
essais successifs conduits à partir de données aléatoires. Elle est
utilisée pour résoudre des problèmes extraordinairement complexes. Où le
hasard répété un grand nombre de fois conduit au déterminisme. Domaine
d'application: intégration,
optimisation, génération de données sous contrainte de loi de probabilité,
etc. |
John
von Neumann, Stanislaw Ulam,
and Nick Metropolis ont utilisé cette méthode à Los Alamos pour la simulation
stochastique (aléatoire) dans le cadre de l'optimisation de la bombe
atomique.
|
|
|
|
||
|
Il s’agit
d’un algorithme de résolution des problèmes d’optimisation linéaire. Un
programme linéaire résume un problème particulier, comme l'optimisation de la
production d'objets, sous la forme d'un système
d'équations. Ce genre
de problème peut être résolu pour les plus simples par l'algèbre ou par
représentation graphique. Pour les cas plus difficiles, on utilise la méthode
de Monte-Carlo
ou la méthode de Simplex ou d'autres méthodes plus récentes. |
Preuve de sa capacité mathématique: À l'université de Berkeley, le
professeur fait part de deux problèmes ouverts en statistiques.
Croyant qu'il s'agissait d'un devoir, Dantzig les a résolus en quelques
jours. Exemple de programme linéaire à résoudre
Algorithme de Simplex Il fonctionne par itérations successives qui sélectionnent les variables
produisant les plus grandes avancées vers la solution minimale. |
|
L'histoire incroyable de George Dantzig
|
Cela se passe en 1939 à la prestigieuse
université de Berkeley en Californie. Ce jour-là, George Dantzig, un étudiant,
arrive en retard en cours de mathématiques. Il s’installe en essayant de se
faire remarquer le moins possible. Sur le tableau noir, il aperçoit deux problèmes
de statistiques inscrits par son professeur. Il ne sait pas trop à quoi ils
correspondent et, étant à la bourre, il n’ose pas demander. Il les note alors
sans rien dire dans son cahie. Il se dit qu’il s’agit de devoirs à faire chez
lui et à rendre au prochain cours. Quelques jours plus tard, il rend sa copie au
professeur, là en encore en retard. Il s’en excuse, mais concède que ses
problèmes étaient plus difficiles que d’habitude. Le prof, occupé, ne relève
pas et prend machinalement la copie de George Dantzig. Il la pose sur son
bureau surchargé de documents en tout genre. Jusqu’ici rien d’exceptionnel. Mais six semaines plus tard, cette histoire prend
une tournure incroyable. Le professeur de mathématiques déboule un dimanche
matin chez George Dantzig, tout excité. Il tend des feuilles à l’étudiant en
lui demandant de les relire avant qu’il ne les publie. George Dantzig
comprend alors : les deux problèmes qu’il avait pris pour des devoirs étaient
en fait deux célèbres énigmes mathématiques, des problèmes de statistiques
encore jamais élucidés à ce jour. Mais lui, sans le savoir, les avait résolu
en deux coups de cuillère à pot. Cette histoire a été immortalisée dans le
film Will Hunting où Matt Damon, tout jeune acteur, y résolvait sans le
savoir, des équations insolubles. Pendant la seconde guerre mondiale, Dantzig est
responsable de statistiques et planification en logistique de l'armée. Il est
à la recherche d'un nouveau modèle mathématique apte à résoudre les problèmes
en un temps raisonnable. Il dit: J'ai commencé à remarquer que la région
réalisable est un corps convexe, c'est-à-dire un ensemble polyédrique. Par
conséquent, le processus pourrait être amélioré si les mouvements étaient
effectués le long des frontières d'un point extrême vers le suivant.
Cependant, cette procédure semblait trop inefficace. En trois dimensions, la
région peut être visualisée comme un diamant avec des faces, des arêtes et
des sommets. Dans le cas de nombreuses frontières, le processus mènerait à un
parcours le long de celles-ci avant que le coin optimal du diamant ne soit
atteint. Le premier problème résolu a
été celui de la nutrition posé par l'armée américaine pour nourrir ses
troupes sous contraintes. Le problème se composait de 9 équations et 77
inconnues. Résolu aussi manuellement, les résultats obtenus furent si proches
que la méthode du Simplexe devint un vétiable succès. George Dantzig est devenu un
des plus grands mathématiciens au monde. En 1975, le président des
États-Unis, Gerald Ford, lui a remis en personne la médaille nationale des
sciences. |
D'après: Florian Gazan – RTL
– 05/01/2022
Et la biographie complète
– PHPSimplex / Original
anglais
|
Méthode de
résolution de systèmes linéaires imposants (sous-espaces de Krylov) – 1950 |
|
|
|
La
résolution de systèmes linéaires très imposants nécessite des factorisations matricielles très coûteuses
(en temps de calcul et mémoire). On utilise alors des méthodes itératives
qui génèrent des résidus de plus en plus petits qui font converger vers la
solution du problème. La méthode fait appel aux puissances successives d'une
matrice (sous-espace de Krylov) Cette
méthode, connue sous le nom GMRES (généralisation de la Méthode de
Minimisation du Résidu), fait partie des méthodes les plus importantes pour
la résolution des systèmes linéaires.
|
Magnus Hestenes, Eduard Stiefel, and Cornelius
Lanczos ont développé cette méthode à l'Institut d'analyse numérique du
Bureau national des Normes à Zurich. Méthode (idée) Résoudre: Ax = b Idée: utiliser la
méthode des sous-espaces de Krylov avec un système aménagé: M-1Ax
= M-1b. Intérêt: il n'est pas
nécessaire de former explicitement la matrice M-1Ax. Il faut
résoudre Mu = z lorsque nécessaire. Impératif: il doit être
facile de résoudre Mu = z pour un vecteur z arbitraire. Sous-espace de Krylov (1931) À partir d'une matrice A (n x n) et un vecteur b
de dimension n, on forme le sous-espace vectoriel dit sous-espace de Krylov. |
|
|
|
||
|
Il s'agit
de filtrer un signal en présence de bruit. Par exemple, le retour d'un écho
radar ou d'un écho sonar ou d'un
signal GPS. Le cerveau fait
cela automatiquement lorsqu'il trie la parole de votre interlocuteur parmi
tous les bruits de la cantine. Il s'agit
donc d'estimer une information (un signal) utile polluée par un bruit
aléatoire, mais dont on estime la loi du comportement. Autrement-dit: il s'agit de trouver l'aiguille dans la botte de foin, tout en
connaissant les caractéristiques de l'aiguille et celles du foin (Utilisation
d'un aimant?). |
Rudolf E. Kalman (1930-2016) est un mathématicien et automaticien
américain. Sa découverte sera
utilisée par la Nasa pour le programme Apollo et la
Navette
spatiale. Intérêt du filtre de Kalman Dans une méthode d'estimation classique (par
exemple, la méthode des moindres carrés), une simple erreur dans la
modélisation du système entraine inévitablement une erreur au niveau de
l'estimation. La force du filtre de Kalman est d'intégrer un
terme d'imprécision sur le modèle lui-même, ce qui lui permet de donner des
estimations correctes malgré les erreurs de modélisation (pour peu que les
erreurs restent raisonnables). Source Ferdinand
Piette |
|
|
|
||
|
Algorithme
qui permet de trouver les valeurs
propres des matrices. Pour
connaitre les solutions d'un système d'équations,
il faut connaitre les valeurs propres de la matrice qui le représente. L'algorithme
consiste à effectuer une factorisation QR, à multiplier les matrices dans
l'autre sens et itérer (recommencer) le processus. Note: Cet algorithme QR n'a rien à voir avec le QR code (Quick
Response). Ici, il s'agit de matrices nommées Q et R. |
Invention: Heinz
Rutishauser (Zurich) Développement: John G. F.
Francis et Vera N. Kublanovskaya, indépendamment. Factorisation QR Décomposition d'une matrice A en un produit: A = QR avec Q est une
matrice orthogonale
et R une matrice triangulaire haute. QT Algorithme (idée)
Sous certaines conditions, la matrice Ak converge vers une
matrice triangulaire et ses valeurs propres figurent sur la diagonale. |
|
|
|
||
|
Un événement
important dans le monde de l'informatique. Un
compilateur réalise l'interface entre un langage évolué (Ici, le Fortran) compréhensible
par l'homme et le langage de base de l'ordinateur
(assembleur), celui qui traduit les directives en instructions binaires,
lesquelles pilotent les circuits électroniques. |
Créateur: John Backus 1954 et l'équipe IBM qui la développé (1957). Fortran est un mot-valise pour
Formula Translator Histoire personnelle En fin des années 1960, le Fortran était en concurrence avec l'Algol.
J'ai débuté l'informatique avec l'Algol. |
|
|
|
||
|
Algorithme
rapide de classement
de listes par ordre alphabétique ou numérique. Cet
algorithme utilise une stratégie récursive: le
programme est vu comme une fonction qui peut faire appel à elle-même (idée de poupées russes). |
Auteur: Tony Hoare d'Elliott Brothers, Limited, Londres Algorithme Un élément de la liste est choisi comme pivot. Les autres éléments
sont triés en piles de données plus grandes ou plus petites que le pivot. le
procédé est répété dans chaque pile avec son propre pivot (récursivité). |
|
|
|
||
|
Les
algorithmes de compression
de données ont rendu les systèmes informatiques moins chers et plus efficaces
au fil du temps. Ils font
gagner en occupation de place mémoire
au prix d'une puissance calcul
supplémentaire. Ils ont
contribué à faire des économies et surtout à assurer la faisabilité de certains
projets comme la transmission des programmes de télévision. |
Compression Les algorithmes de compression sans perte (lossless) restituent
fidèlement les données initiales. Essentiels pour l'archivage de données, par
exemple. Les algorithmes avec pertes (lossy) concernent plutôt les images, le
son et la vidéo. Formats de données avec compression Sans perte: Zip, rar, PNG Avec perte: JPEG, MP3, MPEG-2,
MPEG-4 |
|
![]()
|
Suite |
|
|
Top |
|
|
Voir |
|
|
|
|
|
Cette
page |
![]()