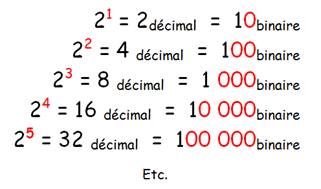Binaire débutants

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/12/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	NUMÉRATION
Débutants Binaire	BINAIRE				Glossaire Général
INDEX Numération	Débutants		Introduction	Conversion
	Magie		Informatique	Table 512
	Code Gray		Numérique	Dualité
		Sommaire de cette page >>> Pair-Impair >>> Exemples >>> Comment cela marche? >>> Petite dose d'arithmétique

NOMBRES BINAIRES

Les ordinateurs ne savent pas compter au-delà de 1.

En fait, ils savent reconnaître

s'il y du courant ou pas;

si un point de sa mémoire est aimanté ou pas.

Donc, deux états seulement:

"il y a" est noté 1, et

"il n'y a pas" est noté 0.

Pour traduire une suite d'états, on notera 1100101100001 …

Un tel nombre est dit binaire, car il ne comporte que deux chiffres, alors que nos nombres habituels en comporte dix, ils sont décimaux.

Il est possible de calculer avec les nombres binaires tout comme avec les nombres décimaux.

Voir Nombre 0 / Nombre 1

Je me lance …

Ouais! Curieux tout cela, même les additions.

En fait, je n'ai rien compris. Voyons cela pas à pas.

Pair-Impair
Vous savez reconnaître les nombres pairs et les nombres impairs, alors vous savez compter en binaire comme les ordinateurs.	Pairs: 0, 2, 4, 6, 8, 10, 12, 14, 16 … Nombres divisibles par 2. Impairs: 1, 3, 5, 7, 9, 11, 13, 15, 17 … Nombres non-divisibles par 2. Divisés par 2, il reste 1.
Dans un nombre binaire, le chiffre des unités est 0 ou 1 selon que le nombre est pair ou impair. En faisant ce premier pas, nous avons fait une moitié de chemin. Normal! Nous sommes dans le monde binaire. On supprime donc une tranche, et on regarde si ce nouveau nombre (3) est pair ou impair. Nous venons de faire une moitié de ce nouveau parcours. On supprime encore une tranche, et On regarde si ce nouveau nombre (1) est pair ou impair. FIN
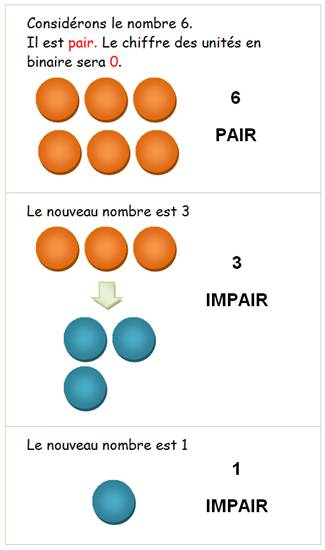
BILAN Compter en binaire consiste à couper le nombre en moitiés successives et à reconnaître si cette moitié est paire ou impaire.	6 divisé par 2 = 3 x 2 + 0 => binaire 0 3 divisé par 2 = 1 x 2 + 1 => binaire 1 1 divisé par 2 = 0 x 2 + 1 => binaire 1 6_décimal = 110_binaire

EXEMPLES
7	7 divisé par 2 = 3 x 2 + 1 => binaire 1 3 divisé par 2 = 1 x 2 + 1 => binaire 1 1 divisé par 2 = 0 x 2 + 1 => binaire 1 7_décimal = 111_binaire
0	0 divisé par 2 = 0 x 2 + 0 => binaire 0 0_décimal = 0_binaire
1	1 divisé par 2 = 0 x 2 + 1 => binaire 1 1_décimal = 1_binaire
2	2 divisé par 2 = 1 x 2 + 0 => binaire 0 1 divisé par 2 = 0 x 2 + 1 => binaire 1 2_décimal = 10_binaire
3	3 divisé par 2 = 1 x 2 + 1 => binaire 1 1 divisé par 2 = 0 x 2 + 1 => binaire 1 3_décimal = 11_binaire

Comment cela marche?

Rien de plus simple. Nous ne disposons que des chiffres 0 et 1 (et non pas 0 à 9).

Alors, au lieu d'aller à 9 et dire 10, l'ordinateur va tout simplement à 1 et, pour le nombre suivant, il va dire 10.

Puis 11

Et comme, il lui est interdit de dire 12 (il ignore totalement l'existence du 2), il va dire tout de suite sauter à 100.

Décimal	M	C	D	U
1				1
2			1	0
3			1	1
4		1	0	0
5		1	0	1
6		1	1	0
7		1	1	1
8	1	0	0	0
9	1	0	0	1
10	1	0	1	0

Observez la régularité de la succession des chiffres des unités (U), des dizaines (D), des centaines (C) et des milliers (M).

Petite dose d'arithmétique

Une partie de la magie de cette mécanique binaire s'explique en faisant intervenir les puissances de 2.

Facile!
Autant de 0 en binaire que la puissance deux en décimal.

Entre deux puissances de deux, des 1 vont apparaître. Eux, aussi, sujet à des puissances de 2.

Les "1" dans un nombre binaire indiquent quelles sont les puissances de deux qu'il faut ajouter.

Décimal	M	C	D	U
10	1	0	1	0
= 8 = 2³	= 1	0	0	0
+ 2 = 2¹	+		1	0

1) La somme en décimal équivaut à la somme en binaire.

2) Les termes de l'adition sont des puissances de deux.

Pour convertir un nombre en binaire on peut procéder comme indiqué en haut, ou

Ajouter les puissances de deux nécessaires en les notant avec un "1"; les absences de puissances de deux seront notées "0".

Décimal	2⁴	2³	2²	2¹	2⁰
23
= 1 x 16	1
+ 0 x 8		0
+ 1 x 4			1
+ 1 x 2				1
+ 1 x 1					1

23_décimal = 10 111_binaire

Les nombres en 10

D'une manière générale un nombre codé en binaire utilise plus de chiffres qu'en décimal.

Notez que les puissances de dix ne sont pas privilégiées. Aucune symétrie particulière. Normal ce sont les puissances de 2 qui sont à la fête dans le monde binaire.

Décimal