|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Base de numération TERNAIRE (base 3) Base utilisée lorsque les choses vont par trois. C'est le cas des pesées avec balance à
plateaux avec trois issues: plateau gauche descend, plateau droit descend ou
équilibre des plateaux. La base ternaire est caractérisée par trois états notés classiquement
par: {0, 1, 2} Autre notation possible plus pratique pour certains emplois: { –1, 0, +1 } ou { –, 0, + } . Cette numération ternaire est dite équilibrée. |
Anglais: Ternary system
|
|
|||
|
La
numération ternaire classique, ou à base
3, utilise les chiffres: 0, 1 et 2. On
compte: 0, 1, 2, 10, 11, 20, 21, 22, 100 … En binaire
on parle de bit; en ternaire, les chiffres sont appelés: trit (trinary
digit). La numération ternaire équilibrée utilisé les
chiffre { –1, 0, +1 }. Le système nonaire
(base 9) permet de regrouper les trits par deux. Un compactage de numération
comme l'octal pour le binaire. |
310 = 103 910 = 1003 2710 = 10003 8110 = 100003 24310 = 1000003 810 = [2, 2]TC = [1, 0, -1]TE = 2x3 + 2x1 = 1x9 – 1x3 |
||
|
Usages |
|
||
Table de conversion décimale / ternaire des
nombres de 0 à 100
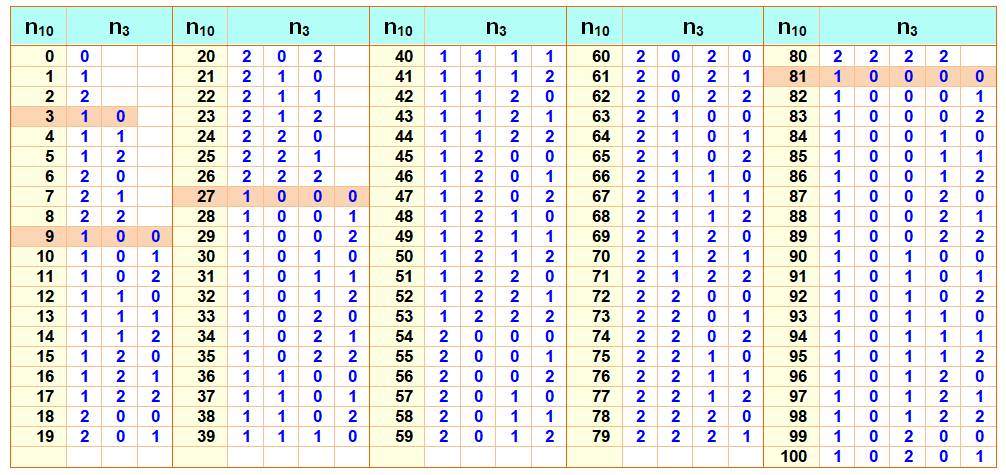
Voir Table – Index
Table de conversion décimale / ternaires classique et équilibré
des nombres de -13 à +13
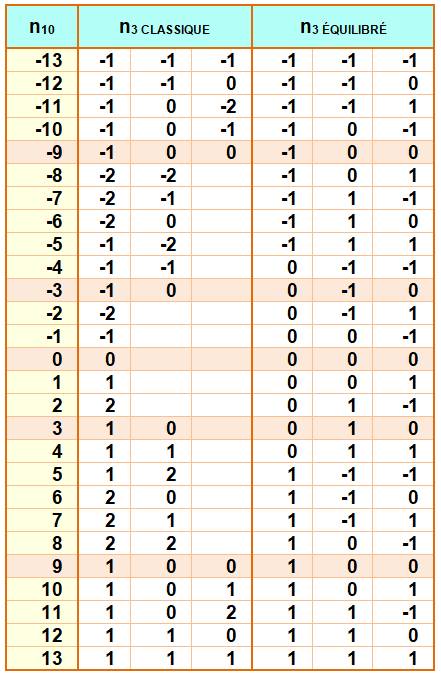
Voir Énigme de la pesée des douze billes
et sa solution ternaire
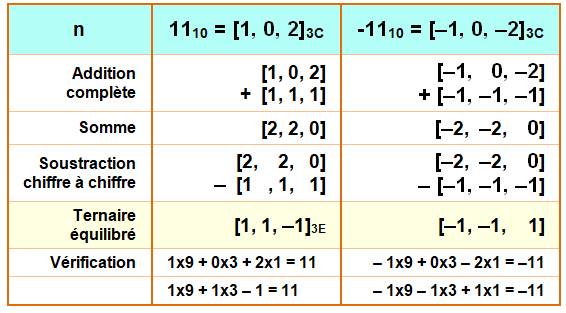
Conversion ternaire classique à ternaire équilibrée
|
On passe de la version classique à
la version équilibrée en ajoutant la constante: 111 … avec retenue (addition
classique, mais ternaire) et en retirant 1 à chaque chiffre (sans retenue).
Pour les nombres négatifs, la constante devient:
[–1, –1, –1, …]. Le principe consiste à transformer tous les 2 en 3 – 1. Exemples
|
![]()
|
|
||
|
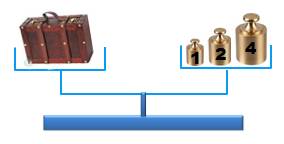
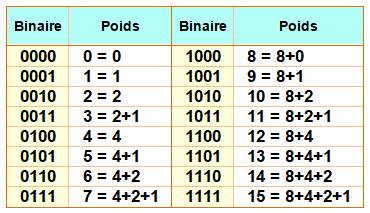
Binaire (Leibniz) Avec des
poids de 1, 2, 4, 8 kg, donc en puissances de 2, il est possible de composer
tous les poids de 1 à 15 kg en utilisant un seul poids de chaque catégorie. Illustration
La valise pèse 4
+ 2 + 1 = 7 kg En binaire: {1,
1, 1} Tableau des pesées
|
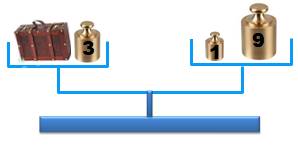
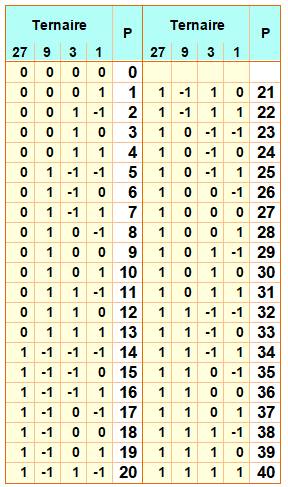
Ternaire ( Bachet) Avec des
poids de 1, 3, 9 et 27 kg, donc en puissances de 3, il est possible de peser
jusqu'à 40 kg en utilisant les poids de chaque côté et, en utilisant un seul
poids de chaque catégorie. Illustration
La valise pèse 9
– 3 + 1 = 7 kg En ternaire
équilibré: {1, –1, 1} Tableau des pesées
Exemple de conversion {1, 1, –1, –1}3
= 27 + 9 – 3 – 1 = 3210 |
|
|
Commentaires Avec le système ternaire à quatre chiffres, on
peut compter de:
La moitié des valeurs sont négatives et ignorées
dans le cas de la pesée et l'autre moitié positive. Soit, les 40 valeurs du
tableau. Conversion décimale du nombre en
ternaire Comme le binaire, la conversion décimale du
ternaire s'obtient en multipliant chaque chiffre { –1, 0 ou +1} par son poids (… 27, 9, 3, 1) |
||
Anglais: Weighing with
counterbalances
|
|
||||||||||||||||||||||||||
|
Leibniz
a démontré qu'on pouvait faire toutes les pesées
possibles avec une série de poids dont chacun est le DOUBLE du précédent. On
ne dispose qu'un seul de chaque, évidemment. Bachet a montré qu'on peut faire la même chose avec des poids TRIPLES, mais
en utilisant les deux plateaux d'une balance. |
|
|||||||||||||||||||||||||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Numerati/aaaBASE/Ternaire.htm
|
![]()