|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère
sans que nous le sachions a priori |
![]()
|
Énigmes de poids avec étiquettes mélangées Le
prétexte de l'énigme est étrange, mais il se prête à quelques énigmes
nécessitant un raisonnement logique. On
commence avec des poids dont la valeur est connue par un étiquetage, mais les
étiquettes ont été mélangées. Suit une
énigme où un bonimenteur connaissant les valeurs des poids, fait l'expérience
devant un public de les retrouver par un minimum de pesées. |
|
|
||
|
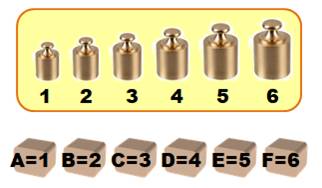
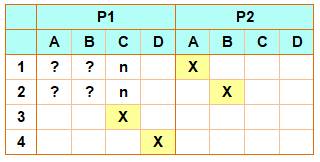
Six poids
de 1 à 6 unités sont enfermés dans des boites identiques. On y a
apposé une étiquette de 1 à 6. En deux
pesées, pouvez-vous vérifier que chaque étiquette correspond bien au poids
qui est dans la boite ? Note: on ne demande pas de remettre les étiquettes en place. |
Les six poids et les six
boites avec étiquettes (vraies ou fausses)
|
|
|
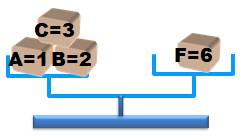
La première pesée Elle se
base sur le fait que: 1 + 2 + 3 = 6, seule possibilité. Elle
permet de départager deux lots:
- étiquette 6: bien placée; - étiquettes (1, 2 et 3) en désordre sur les
poids A, B et C; et - étiquettes (4 et 5) en désordre sur les poids D
et E. |
Les poids dans les boites corespondent-ils à la valeur indiquée sur
l'étiquette ? Oui, s'il y a équilibre. |
|
|
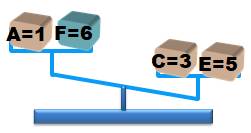
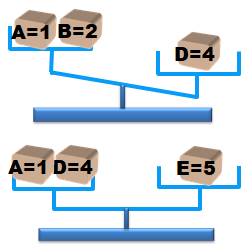
La seconde pesée Elle est plus
subtile. Elle utilise le poids F = 6 qui est maintenant connu. On
installe:
Si les étiquettes étaient à la bonne place, cette
pesée donnerait: 1 + 6 = 7 versus 3 +
5 = 8 et la balance pencherait à droite. Bien! Mais, existe-t-il d'autres possibilités ? En faisant la revue de toutes les associations
d'étiquettes aux valeurs possibles, la seule qui fera pencher la balance à
droite est celle qui est la bonne: 1 + 6 vs 3 + 5 (rouge) |
Possibilités pour A = (1, 2, 3) Possibilités pour C = (1, 2, 3) Possibilités pour E = (4, 5) Pesées possibles 1 + 6 = 7 vs 2 + 4 = 6 => penche à gauche 2 + 6 = 8 vs 1 + 4 = 5 => penche à gauche 3 + 6 = 9 vs 1 + 4 = 5 => penche à gauche |
|
![]()
|
|
||
|
Le
bonimenteur d'adresse à un public et se met lui-même au défi de retrouver les
poids en un minimum de pesées. Le tour
de force réside dans le fait que la valeur des poids est cachée et aucun
indice ne laisse supposer sa valeur. Oui,
mais! Le bonimenteur, lui, connait les valeurs. En
résumé: le bonimenteur sait et le public ne sait pas. |
Poids de 1, 2, 3 ... n fois 100
grammes, par exemple. Selon le nombre n de poids, trouver la quantité de minimale de pesées
P(n) pour retrouver les poids cachés. Tout l'art de ce tour consiste à montrer au public que la déduction
est logique et que les pesées proposées produisent bien le résultat escompté.
Oui! L'audience doit avoir un esprit très logique pour apprécier. |
|
|
Avec 2 poids: 1 et 2 Aucune
magie, le tour est évident. Le
bonimenteur sachant que poids 1 est dans la boite A, place A à gauche et B à
droite. Inutile
d'ouvrir les boites pour confirmer le
résultat. |
Le poids d'une unité est à gauche et celui de deux unités est à
droite. |
|
|
Le
bonimenteur fait les deux pesées indiquées et dit que A contient le poids 1, B
le 2 et C le 3. L'ouverture des boites prouve l'affirmation. Mais
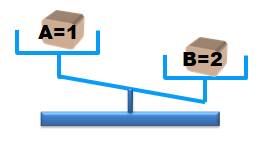
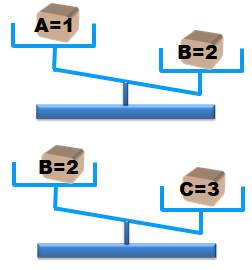
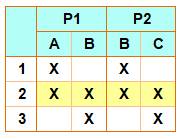
pourquoi est-ce sans discussion ? Tableau des pesées et déductions Lors de
la première pesée, on déduit que A peut contenir le poids 1 et B le poids 2;
mais tout aussi bien: A = 2 et B = 3 Avec la
deuxième pesée, on déduit de la même manière que (B = 1 et C = 2) ou (B = 2
et C = 3). Mais, du fait de la première pesée, B n'est pas égal à 1. Reste (B
= 2 et C = 3). Logiquement A < B < C. Note: c'est la
transitivité des inégalités. |
NB: les étiquettes montrées au public sont A, B et C; les valeusr
associées ne sont connues que du bonimenteur
|
Point
|
Ces
deux exemples sont très simples. Ils permettent de comprendre ce qui est
cherché avec ces énigmes. Le cas n = 4 va demander un peu plus de recherche. |
|
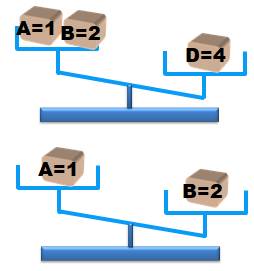
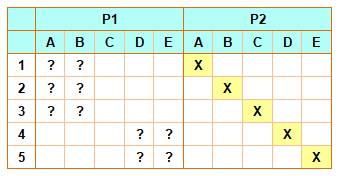
Le
bonimenteur effectue les deux pesées indiquées. L'ouverture des boites
montrent que les égalités indiquées (non connues du public) sont satisfaites. Mais
pourquoi est-ce la bonne logique ? Comme
précédemment, on va noter le poids potentiels de chaque boite à l'issue de
chaque pesée. Tableau des pesées et déductions Seul D =
4 convient à la première pesée. On le vérifie en considérant toutes les
possibilités:
Le 3
n'intervient pas dans la seule pesée possible (1+2 vs 4), c'est que C = 3. La
deuxième pesée départage A = 1 et B = 2. |
|
|
Le
bonimenteur effectue les deux pesées indiquées. Tableau des pesées et déductions Pour la
première pesée, le plateau droit descend pour:
Conclusion
deux lots: (1, 2, 3) et (4, 5). La
deuxième pesée indique que D < E, alors D = 4 et E = 5.
Bilan:
avec ces deux pesées la seule solution correspond bien aux égalités indiquées
sur le dessin (qui, je le répète, ne sont pas connues du public). |
|
|
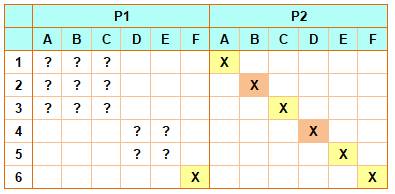
Avec 6 poids: 1, 2, 3, 4, 5
et 6 Le
bonimenteur effectue les deus pesées indiquées. Comme pour la première
énigme Tableau des pesées et déductions En
première pesée, l'équilibre est atteint uniquement pour F = 6. Ce qui partage
les autres en deux lots (1, 2, 3) et (4 et 5). Pour la
seconde pesée, nous avions vu que la seule possibilité pour faire pencher la
balance à droite est d'y placer 3 + 5 = 8 et 1+ 6 à gauche. Nous
avons: A = 1, C = 3, E = 5 et F = 6. Or B est
dans le lot (1, 2, 3) donc B = 2 et D = 4. |
|
|
L'article
en référence de Tanya Khovanova and Joel Brewster Lewis traite
de ce problème et annonce que:
L'article
présente la solution trouvée par Konstantin Knop pour n = 15 en trois pesées.
La propriété suivante est utilisée pour la première pesée: 1 + 2 + 3 + 4 + 5
+ 6 + 7 = 28 & 14 + 15 = 29 Seul
cas où la balance penche à gauche pour sept poids contre deux. |
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette
page |
![]()