|
|||||||||||||||||||||||||||||||||
![]()
|
Nombres
premiers PERMUTABLES ou
CIRCULAIRES ou ROBUSTES
|
Anglais: Permutable prime
numbers
|
ou
CIRCULAIRES ou ROBUSTES |
|
|||||||
|
Définitions Premiers permutables: nombre premier qui
reste premier par permutation circulaire
de ses chiffres. Premier presque permutables: toutes les
permutations sont des nombres premiers, sauf une.
|
Exemples de premiers
permutables
|
|||||||
|
Les quatre permutables à deux chiffres
(hors le repdigit
11) sont aussi Emirp. Coquetterie
pour le couple (37, 73) qui permutent aussi leur rang en tant que premiers
(12, 21). |
|
|||||||
|
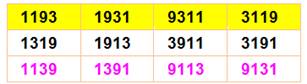
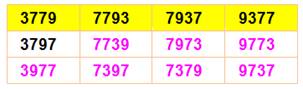
Exemple avec les deux nombres à quatre
chiffres:
|
|
|||||||
Voir Nombres retournés et premiers
|
|
|
|
|
|
|
|
|||
|
Longueur
1 031 Total = ? |
|
Rep-unit 1
031 = (101 031 - 1)/9 |
|
|
Longueur
317 Total = ? |
|
Rep-unit 317
= (10317 -1)/9 |
|
|
Longueur
23 Total = ? |
|
11 111 111 111 111 111 111 111 |
|
|
Longueur
19 Total = ? |
|
1 111 111 111 111 111 111 |
|
|
|
Autres: voir site de De
Geest |
||
|
Longueur
10 Total = 0 |
|
|
|
|
Longueur
9 Total = 0 |
|
33 191 nombres premiers candidats |
|
|
Longueur
8 Total = 0 |
|
9 177 nombres premiers candidats |
|
|
Longueur
7 Total = 0 |
|
2 709 nombres premiers candidats |
|
|
Longueur
6 Total = 2 |
|
757 nombres premiers candidats |
|
|
Longueur
5 Total = 2 |
|
249 nombres premiers candidats |
|
|
Longueur
4 Total = 2 |
|
63 nombres premiers candidats |
|
|
Longueur
3 Total = 3 |
|
30 nombres premiers candidats |
|
|
Longueur
2 Total = 5 |
|
10 nombres premiers candidats |
|
|
Longueur
1 Total = 4 |
|
|
|
|
|
|
|
Un premier REIMERP ou EMIRP (premier ou prime épelés à
l'envers) sont des nombres premiers qui restent
premiers en les retournant, comme 13 et 31. Chacun de ses nombres premiers trouve son double
retourné dans cette liste (exemple avec les premiers en rouge). Ils sont 1
229 sans compter les repdigits
(exclus de la définition). 13, 17, 31,
37, 71, 73, 79, 97, 107, 113, 149, 157, 167, 179, 199, 311, 337,
347, 359, 389, 701, 709, 733, 739, 743, 751,
761, 769, 907, 937, 941, 953, 967, 971, 983, 991, 1009, 1021, 1031, 1033, 1061, 1069, 1091, 1097,
1103, 1109, 1151, 1153, 1181, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237,
1249, 1259, 1279, 1283, 1301, 1321, 1381, 1399, 1409, 1429, 1439, 1453, 1471,
1487, 1499, 1511, 1523, 1559, 1583, 1597, 1601, 1619, 1657, 1669, 1723, 1733,
1741, 1753, 1789, 1811, 1831, 1847, 1867, 1879, 1901, 1913, 1933, 1949, 1979,
3011, 3019, 3023, 3049, 3067, 3083, 3089, 3109, 3121, 3163, 3169, 3191, 3203,
3221, 3251, 3257, 3271, 3299, 3301, 3319, 3343, 3347, 3359, 3371, 3373, 3389,
3391, 3407, 3433, 3463, 3467, 3469, 3511, 3527, 3541, 3571, 3583, 3613, 3643,
3697, 3719, 3733, 3767, 3803, 3821, 3851, 3853, 3889, 3911, 3917, 3929, 7027,
7043, 7057, 7121, 7177, 7187, 7193, 7207, 7219, 7229, 7253, 7297, 7321, 7349,
7433, 7457, 7459, 7481, 7507, 7523, 7529, 7547, 7561, 7577, 7589, 7603, 7643,
7649, 7673, 7681, 7687, 7699, 7717, 7757, 7817, 7841, 7867, 7879, 7901, 7927,
7949, 7951, 7963, 9001, 9011, 9013, 9029,
9041, 9103, 9127, 9133, 9161, 9173, 9209, 9221, 9227, 9241, 9257, 9293, 9341,
9349, 9403, 9421, 9437, 9439, 9467, 9479, 9491, 9497, 9521, 9533, 9547, 9551,
9601, 9613, 9643, 9661, 9679, 9721, 9749, 9769, 9781, 9787, 9791, 9803, 9833,
9857, 9871, 9883, 9923, 9931, 9941, 9967. Les
suivants: 10 007, 10 009, 10 039 … |
|
Voir Nombres
premiers et retournés – Table
|
|
||
|
|
On ouvre une liste vide (L). Recherche des premiers permutables de 1 à 200 que
si n est un nombre premier. Après conversion, N est la liste des chiffres de
n. Addition pondérée par la puissance de 10 qui va
bien pour obtenir le retourné de n en m. L'instruction add agit comme une
boucle avec les valeurs de i successives de 1 à q; q étant la quantité de
chiffres (nops) dans L. Si m, le retourné de n, est premier, on introduit
n dans la liste L. Ici, nous avons fait le choix de mentionner aussi m. Le
fait de mettre des accolages { } indique que les doublons doivent être
éliminés (liste de type ensemble). En fin de condition "si premier" et en
fin de boucle, on imprime la liste. |
|
Voir Programmation des permutations / Programmation – Index
![]()
|
Voir |
|
|
Aussi |
|
|
voir site de Patrick De Geest |
|
|
Cette page |
![]()