|
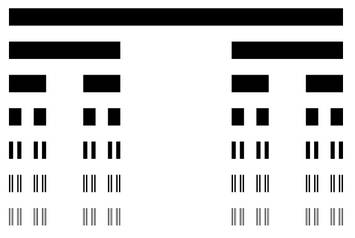
 Prendre un segment, lui retirer son tiers central.
Prendre un segment, lui retirer son tiers central.
 Prendre chacun des deux segments restants et leur
retirer le tiers central.
Prendre chacun des deux segments restants et leur
retirer le tiers central.
 Etc.
Etc.

Etc.
 En continuant, on forme une poussière de points.
En continuant, on forme une poussière de points.
 Il y en a une infinité.
Il y en a une infinité.
 La longueur totale est nulle.
La longueur totale est nulle.
 Ces propriétés paradoxales ont perturbé les
mathématiciens du XIXe siècle.
Ces propriétés paradoxales ont perturbé les
mathématiciens du XIXe siècle.
 Si vous lancer une fléchette sur une ligne des plus
basses, la probabilité d'atteindre un tiret noir tend vers zéro, car la
longueur cumulée des tirets tend vers zéro.
Si vous lancer une fléchette sur une ligne des plus
basses, la probabilité d'atteindre un tiret noir tend vers zéro, car la
longueur cumulée des tirets tend vers zéro.
 La quantité de tirets augmente pourtant jusqu'à devenir
indénombrable comme l'infini des
nombres réels.
La quantité de tirets augmente pourtant jusqu'à devenir
indénombrable comme l'infini des
nombres réels.
Générateur: 3 segments de longueur 1/3
Longueur: Nulle
Dimension: log 2 / log 3 = 0,630 9...
 Mandelbrot utilise cet ensemble comme modèle de
probabilité d'erreurs sur les lignes de transmission électronique. Il avait
observé qu'il y avait des bouffées d'erreurs, et non une continuité
d'erreurs, et ce, à toutes les échelles de temps.
Mandelbrot utilise cet ensemble comme modèle de
probabilité d'erreurs sur les lignes de transmission électronique. Il avait
observé qu'il y avait des bouffées d'erreurs, et non une continuité
d'erreurs, et ce, à toutes les échelles de temps.
|
![]()
![]()
![]()