Défis divers avec le demi-cercle

Édition du: 30/01/2025

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Double triangle rectangle
	Nappe sur table	Triangle rectangle partagé	Rectangle et triangle
	Carré oblique	Carré et triangle équil.	Triangles dans triangle
	Quart de cercle	Cercle et demi-cercles	Deux demi-cercles
	Quatre cercles et carré	Demi-cercle – Divers	Cercle et demi-cercle

DEMI-CERCLE

Florilège de défis

Quelques défis simples de géométrie. Impliquant principalement le demi-cercle ou le quart de cercle.

Sommaire de cette page

>>> Quadrilatère inscrit dans le demi-cercle

>>> Quart de cercle et demi cercle

>>> Carré dans le quart de cercle

Débutants

Géométrie

Glossaire

Géométrie

Quadrilatère inscrit dans le demi-cercle		haut
Proportions et Pythagore à l’œuvre. Plus une équation du second degré à résoudre.
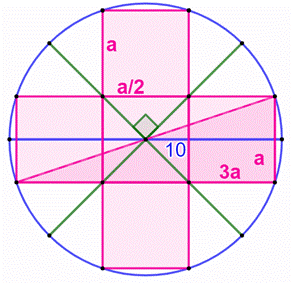
Construction Un quadrilatère inscrit dans un demi-cercle. Deux des côtés ont la même longueur. Quel est le rayon du cercle en fonction des mesures a et b ? Piste (Figure du bas) Le triangle ADB est inscrit dans un demi-cercle, il est rectangle en D. Le quadrilatère DCBE, avec des côtés égaux par paires, est un cerf-volant, un. Ses diagonales se coupent à angle droit. Le triangle EFB est un triangle rectangle en F et il est semblable au triangle ADB. Alors EF = a/2.	Figure Figure avec notations
Calculs Applications numériques

Quart de cercle et demi cercle		haut
Problème très simple à condition de ne pas s'embarquer dans des calculs trop tôt.
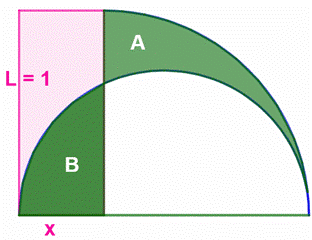
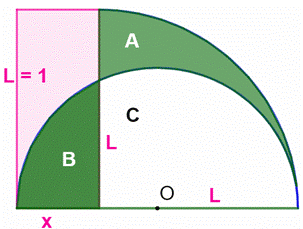
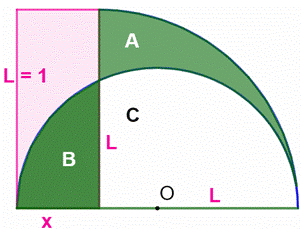
Construction Un rectangle de dimensions (L et x). Un quart de cercle construit sur la sa longueur et un demi cercle tel que sur la figure. Quelle est la valeur de x pour que les aires A et B soient égales ? Donner la valeur de l'aire. Pistes Notons C la zone circulaire blanche : B + C = demi-cercle de diamètre (x + L). A + C = quart de cercle de rayon L. Nous devons obtenir A + C = B + C Calculs Aires : A + C = ¼ π L² B + C = ½ π (½ (L + x))² En égalant huit fois les égalités: 2π L² = π (L² + 2Lx + x²) x² + 2Lx – L² = 0 (x + L)² – 2L² = 0 x + L = √2 L x = (√2 – 1) L = 0,4142... L	Figure initiale avec L = 1 Figure avec notations
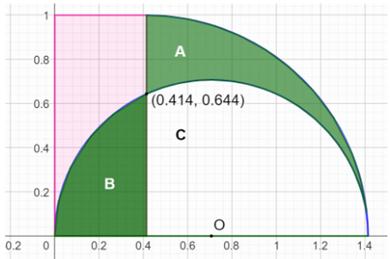
Calcul de l'aire des zones vertes La zone B est en fait un demi-segment de disque. Son aire: Avec R = √2/2 et h = √2/2 – (√2 – 1) = 1 – √2/2 Pour L = 1, le calcul donne: A = B = 0,191677238… cm²	Illustration avec GeoGebra

Carré dans le quart de cercle		haut
Une petite construction pour y appliquer Pythagore ou, plus astucieux, une extension de construction.
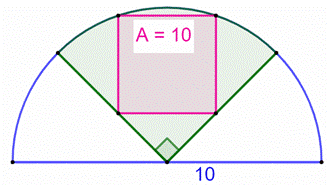
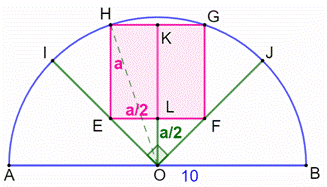
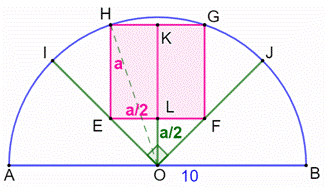
Construction Un quart de cercle (vert) dans lequel est inscrit un carré (rose). Cercle de diamètre 10 cm. Montrer que l'aire du carré vaut 10 cm². Pistes La bissectrice OK de l'angle droit IOJ partage le carré en deux rectangles de côtés (a et a/2). Les triangles EOF et ELO sont isocèles rectangles et : EL = LO = a/2. Côté a du carré Avec le théorème de Pythagore dans le triangle rectangle HKO : HO² = r² = 5² = (a/2)² + (a + a/2)² 4 × 25 = a² + 9a² = 10a² a² = 10 ( qui est l'aire du carré) a = √10 = 3,16 22 77 66 ...	Figure initiale Figure avec notations
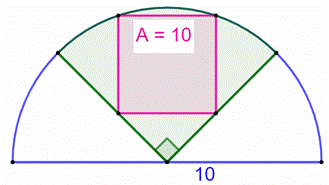
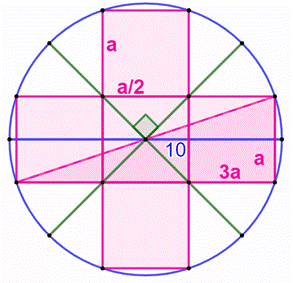
Solution originale Le demi-cercle est complété et les carrés reproduit en quatre exemplaires, plus un carré au centre qui est isométriques aux autres (cf. triangles isocèles rectangles tels que vus ci-dessus). Considérons un rectangles formés de trois carrés et sa diagonale et appliquons de théorème de Pythagore : 10² = a² + 9a² a² = 10	Nouvelle figure

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/TrgDiv.htm