|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
HIDATOTM ou HIDAKU Jeu
avec des nombres à placer sur une grille. Les nombres successifs doivent
former une chaîne continue.
Inventé
par Gyora Benedek, un mathématicien israélien. Hida en hébreux veut dire énigme (riddle en anglais). |
|
|
||
|
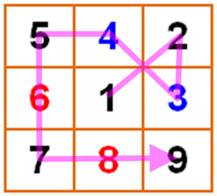
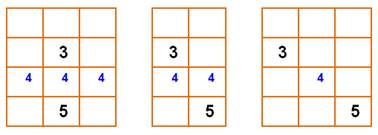
Cette
grille de 3 x 3 doit être complétée pour contenir les nombres de 1 à 9 de
façon à former une chaîne de nombres successifs en horizontal, en vertical ou
en diagonal. Deux
cas sont évidents:
Reste
à placer le 3 et le 4 Seule possibilité: passer par les diagonales. La
chaîne requise est satisfaite:
|
Grille et sa solution en deux étapes
|
|
|
|
||
|
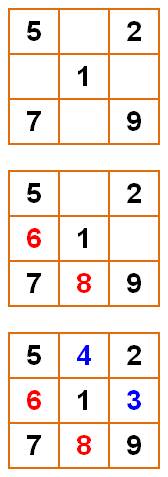
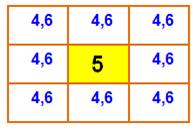
En
présence d'un nombre comme le 5, le 4 et le 6 peuvent se trouver dans l'une
de huit cases contigües. |
|
|
|
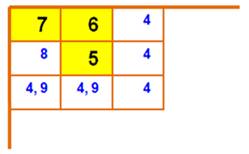
En
présence de cette configuration avec 5, 6 et 7, le 8, successeur du 7, ne
peut se trouver que dans la case indiquée. Les cases voisines sont complétées
par le successeur du 8 (deux positions) et le prédécesseur du 5 (cinq
positions). |
|
|
|
Avec
le 5 en dessous du 3, trois possibilités pour le 4. S'il
est déporté d'une case, deux possibilités S'ile
déporté en diagonale, une seule possibilité. |
|
|
|
|
||
|
Cette
forme de grille en nid d'abeille est fréquente. Sa
résolution est très simple.
|
Grille et sa solution
|
|
|
|
||
|
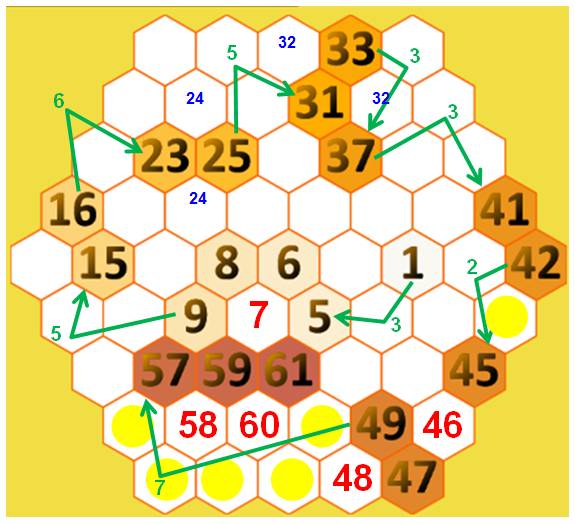
Compléter
cette grille avec les nombres de 1 à 61. Notez
que, cette fois, chaque case n'a plus que six
voisins au lieu de huit dans les grilles rectangulaires. |
|
|
![]()
Solutions
|
|
||
|
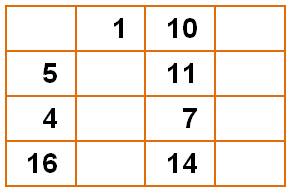
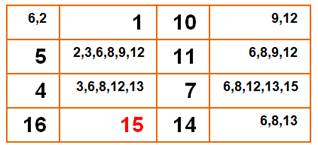
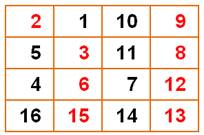
Entre
le 16 et le 14, vient naturellement le 15.
Pour
cette fois, positionnons les nombres possibles dans les cases vides. Il
reste à trouver un chemin qui part du 1 pour arriver au 16. Et
nous avons la solution. Avec
l'habitude, ce raisonnement est fait mentalement. |
|
|
|
|
||
|
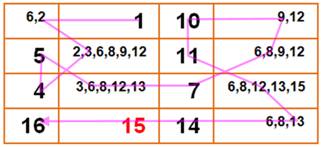
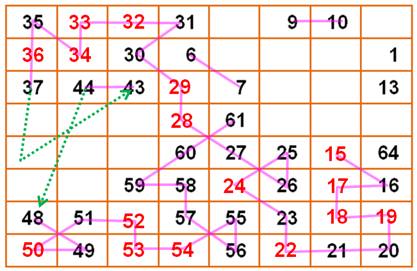
En
violet les suites qu'il est possible de créer avec les nombres de l'énoncé. En
vert, les chemins qui s'imposent pour rejoindre un nombre à un autre:
Par ailleurs, rejoindre 23 à 25 n'offre qu'une possibilité au 24. Pour
aller de 17 à 20, il faut réserver deux places; ce qui implique que le 22
trouve sa place. |
|
|
|
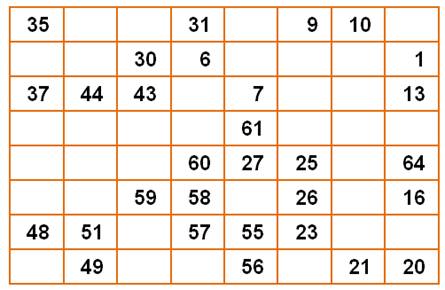
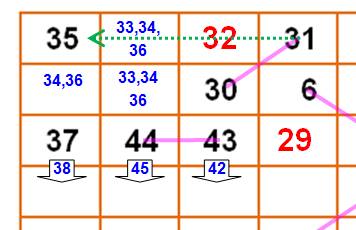
Analyse
du coin haut gauche.
Les
suites de 37, 43 et 44 se situeront vers le bas. Avant
le 30, le 29 trouve sa place dans la seule case libre. |
|
|
|
Les
33, 34, 36 sont placés (plusieurs possibilités). Le
28 rejoint 27 et 29. Le
chemin de 48 à 54 est complété sans difficulté. De
même que de 17 à 20. |
|
|
|
La
poche vide à gauche au milieu se remplit facilement. On rejoint 37 à 43 en
laissant le chemin libre pour rejoindre 44 à 48. La
poche en haut à droite n'est guère plus difficile au risque de quelques
tentatives avortées. |
|
|
|
|
||
|
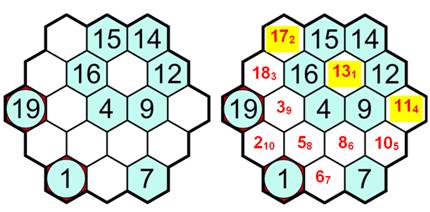
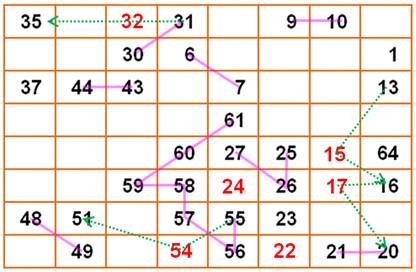
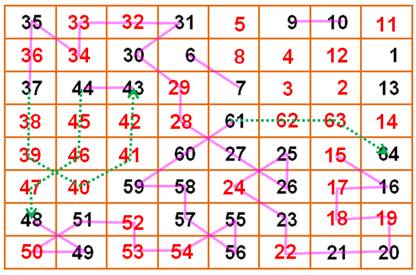
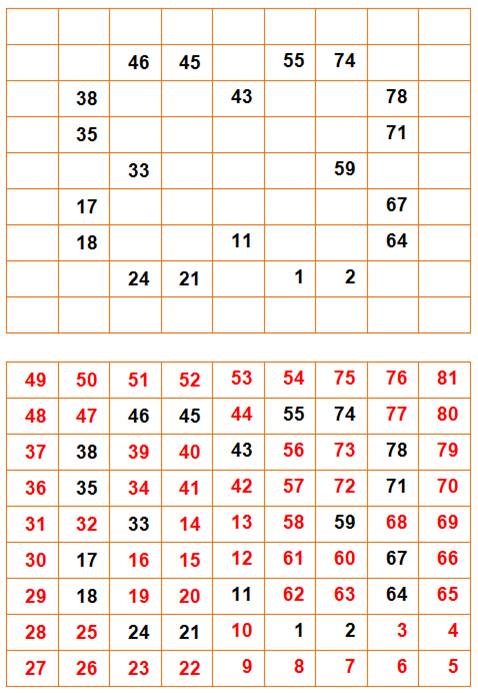
Une
aide au raisonnement est ici nécessaire. Il faudrait beaucoup de chance pour
y arriver par essais et erreurs. D'abord
nous cherchons si certains nombres peuvent être placés (rouge). Ensuite,
nous indiquons les connexions à réaliser en matérialisant une chaîne (ligne
verte) indicée de la quantité de nombres dans la chaîne. En
passant nous plaçons un pion jaune dans les cases qui seront obligatoirement
occupées par la chaîne. Pour
finir ce travail de préparation, nous indiquons en bleu les nombres qui ne
peuvent être placés que sur deus cases. |
|
|
|
La
chaîne 9 à 15 nécessite cinq cases libres, or il n'y en a que cinq possible. Il
ne reste qu'une possibilité pour le 10, puis le 17, 18, 19 … À
partir de 57, nous plaçons la chaîne 57 à 49 sans difficulté. À
partir de 25, la chaîne de 5 se place naturellement. Elle relègue le 32 à
droite du 31. Ce
qui impose la position de la chaîne 33 à 37; puis celle de 37 à 41. Les
cinq dernières cases deviennent évidentes. |
|
|
|
Jeux d'enfants Il
s'agit bien d'un jeu de labyrinthe numérique. La solution n'est pas
unique. La résolution nécessite parfois
des tentatives par essais erreurs. Jeux d'adulte La
grille peut prendre des formes diverses et certaines cases, comme dans les mots croisés, peuvent être noires
(interdites). Parmi les nombres donnés figurent le 1 et le final. Une grille
bien formée conduit à une solution unique entièrement déductible par raisonnement
logique. Comme pour le Sudoku, le niveau de
difficulté peut être très élevé. Numbrix Jeu
identique sauf que les successions par les diagonale sont interdites. Jeu
inventé par Marilyn Vos Savant. Exemple ci-dessous. Les
noms Hidato et Numbrix sont des marques déposées (registered trademarks -
TM). |
|
|
||
|
On
rappelle que la succession des nombres n'est possible qu'en horizontal et en
vertical; interdite en diagonale. Cette
énigme vous paraitra simple à résoudre. Il n'y a effectivement que quatre
possibilités autour d'une case. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()