NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/01/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Jeux et énigmes
Débutants Général	Combinatoire				Glossaire Général
INDEX Partitions Jeux Combinatoire	Escalier 2	Escalier 3	Timbres	Abeille
	Parties de jeu	Tournois	Lapins	Croix
		Sommaire de cette page >>> Partition 1/2/3 de 1 à 5 >>> Partition 1/2/3 de 6 à 10 >>> Exemples de calcul >>> Bilan

ESCALIER qui mène à FIBONACCI

Décomposition d'un entier sous contraintes

(2/2)

Nous poursuivons l'exploration de la montée d'escalier avec la possibilité de monter trois marches d'un coup. Avec une ou deux marches nous avons vu que:

le problème est équivalent à celui de la partition d'un nombre en utilisant que des 1 ou des 2.

la quantité de trajets possibles sur l'escalier – ou de partitions avec 1 et 2 – est un nombre de la suite de Fibonacci.

Que se passe-t-il avec 3 marches?

problème équivalent à celui de la partition avec les nombres 1, 2 et 3.

la quantité est la suite de tribonacci.

Avec 4 marches, ce sera le tour des tétranacci.

Partition 1/2/3 des nombres de 1 à 5

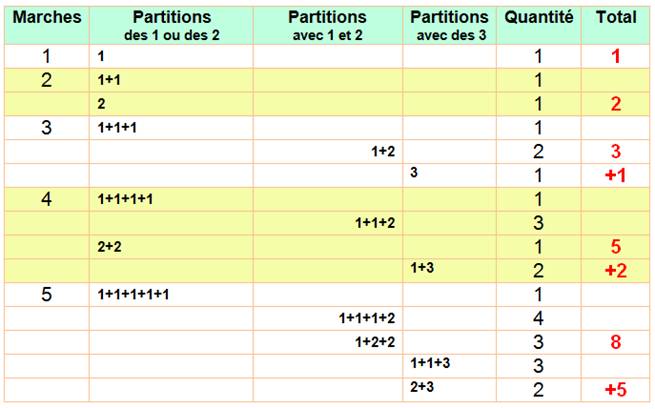
Le tableau montre les partitions obtenues avec les seuls nombres 1 et 2 qui restent valables et celles qui sont engendrées par l'arrivée du nombre 3. Le dénombrement est simple jusqu'ici: n = 3 => Je monte les trois marches toutes d'un coup et je n'ai qu'une possibilité de faire cela. n = 4 => Je monte une marche puis trois ou trois puis une, soit deux possibilités. n = 5 => Je monte une marche puis une puis trois. résume en 1 + 1 + 3. Or, je peux monter trois marches d'abord ou en deuxième ou en troisième lieu. Soit trois possibilités. n = 5 => Avec deux et trois marches, je monte deux d'abord ou trois d'abord, soit deux possibilités. Après cette familiarisation, nous verrons comment calculer le nombre de cas à la simple vue de la partition.

Partition 1/2/3 des nombres de 6 à 10
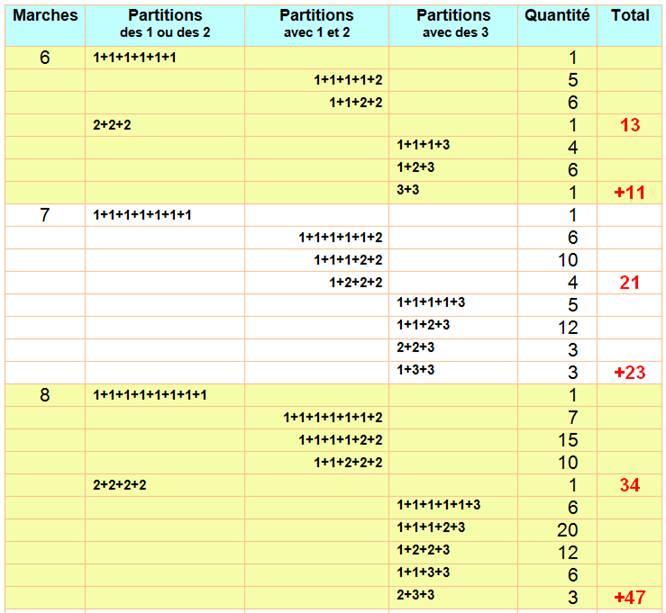
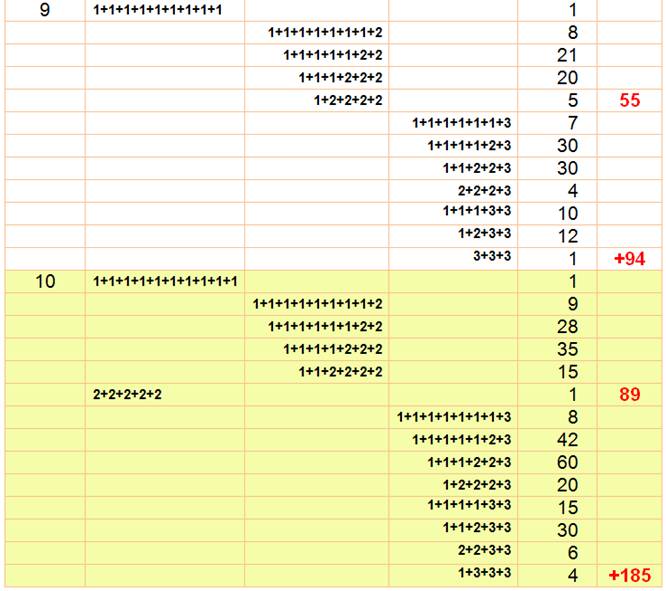
Voici le tableau; des exemples de calculs sont explicités ci-dessous.

Exemples de calcul pour le 7
7 = 1 + 1 + 1 + 3 4 possibilités	Le 3 peux occuper n'importe laquelle des quatre positions dans l'addition. 7 = 1 + 1 + 1 + 4 7 = 1 + 1 + 4 + 1 7 = 1 + 4 + 1 + 1 7 = 4 + 1 + 1 + 1
7 = 1 + 1 + 2 + 3 12 possibilités	Utilisons la méthode des permutations. Quatre objets: 4! Détails: Je tire les quatre objets l'un après l'autre. J'ai quatre possibilités de placer le premier. Je tire le suivant et le place sur l'une des trois positions restantes. Je tire le troisième, me reste deux positions. Le quatrième se place sur l'unique position restante. Bilan pour quatre objets: 4x3x2x1 = 4! possibilités Dont deux identiques : 2! Détails: Nous observons que les deux 1 sont interchangeables. Il y a 2! 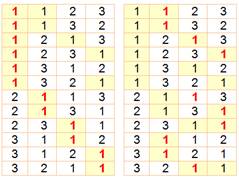possibilités de les permuter. Autant de permutations à supprimer. Bilan: 4! / 2! = 12. Détails: En combinatoire, les choses se multiplient ou se divisent. Pour se convaincre du résultat, voici les combinaisons: Le fait d'échanger un 1 (rouge) par l'autre (noir) provoque le doublement des possibilités.
7 = 2 + 2 + 3 3 possibilités	Trois objets: 3! Le 2 est doublé: 2! Bilan: 3! / 2 ! = 3
7 = 1 + 3 + 3 3 possibilités	Trois objets: 3! Le 3 est doublé: 2! Bilan: 3! / 2 ! = 3

Bilan

Ce tableau donne les possibilités de monter n marches d'escalier par 1 ou 2 (avec 2) et par 1ou 2 ou 3 (avec 3) marches. On retrouve en bas du tableau la suite de tribonacci: chaque nombre est la somme des trois précédents: D(n+1, 3) = D(n, 3) + D(n–1, 3) + D(n–2, 3) Cette formule de récurrence s'explique de la même façon que celle que nous avons mise en évidence avec deux 2 nombres >>> La généralisation est faisable: un N-bonacci de rang n donne la quantité de partitions du nombre n avec les nombres de 1 à N >>> Voir comment produire ces nombres par polynômes générateurs >>>

Merci à Jérôme Bastien pour la correction apportée au bilan et aux conclusions à en tirer

Retour	Escalier avec deux marches Partitions – Quantité
Suite	Partitions – Fonctions génératrices Partitions – Index
Voir	Escalier roulant Fibonacci et partitions Jeux et énigmes - Index Méandres Papier plié Parcours du taxi en ville Partage – Énigmes classiques
DicoNombre	Nombre 14
Site	OEIS A000073 – Tribonacci numbers
Cette page	http://villemin.gerard.free.fr/aJeux1/Combin/Escalie3.htm