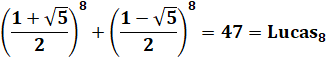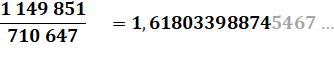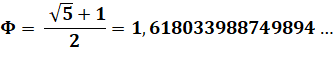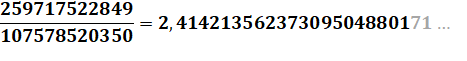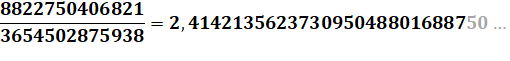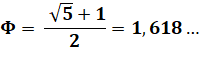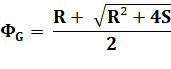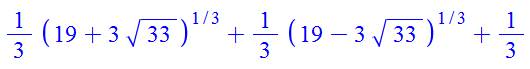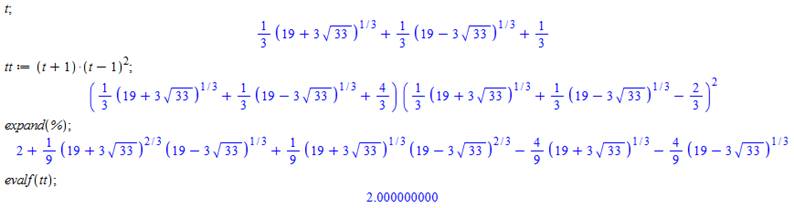NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 21/02/2025

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

             

ITÉRATIONS

 

Débutants

Fibonacci

Nombres de

FIBONACCI et Cie

 

Glossaire

Suite et série

 

 

INDEX

 

Fibonacci

 

Itérations

 

Fibonacci

Lucas

Padovan

F. Généralisée

 

Sommaire de cette page

>>> Suites classiques – Liste

>>> Suite de Lucas

>>> Suite de Pell

>>> Suite de Fibonacci généralisée

>>> Lucas & Fibonacci

>>> Tribonacci

>>> Fibonacci puissance

>>> Somme rationnelle

 

 

 

 

Suite de Fibonacci / Lucas / Pell

et quelques autres

  

Cousine de la suite de Fibonacci avec des chiffres différents au départ et un calcul de somme pondérée.

 

Suite de LUCAS Nombre de Fibonacci avec 1 et 3 au départ.

Anglais: Lucas numbers

 

Suite de PELL Nombre de Fibonacci "double".

Anglais: Pell numbers

Voir / Édouard Lucas (1842-1891)

 

 

Devinette – Solution

Comment montrer que:

Voir Solution pour toutes les puissances

Pour info, formulation LaTex

\left(\frac{1+\sqrt{5}}{2}\right) ^{8}+\left(\frac{1-\sqrt{5}}{2}\right) ^{8} = 47

 

Voir Comment s'y prendre avec GeoGebra

  

Autres énigmes

 

 

Suites récurrentes classiques

Fibonacci

(1, 1 / 1, 1)

Fn = Fn – 1 + Fn – 2

>>>

n-step Fibonacci

Somme de n termes précédents.

Tribonacci pour n = 3, etc.

>>>

Généralisé

(a, b / R, S)

Fn = R.Fn – 1 + S.Fn – 2

>>>

Lucas

(1, 3 / 1, 1)

Ln = Ln – 1 + Ln – 2

>>>

n-step Lucas

Somme de n termes précédents.

La suite classique de Luca est 2-step Lucas.

>>>

Pell

(0, 1 / 2, 1)

PEn = 2 PEn – 1 + PEn – 2

>>>

Pell-Lucas

(1, 2 / 2, 1)

PLn = 2 PLn – 1 + PLn – 2

>>>

Padovan

(1, 1, 1 / 0, 1, 1)

Pn = Pn – 2 + Pn – 3

>>>

Perrin

(3, 0, 2 / 0, 1, 1)

PRn = PRn – 2 + PRn – 3

>>>

Voir Fibonacci et ses cousines – Illustration

 

Illustration géométrique

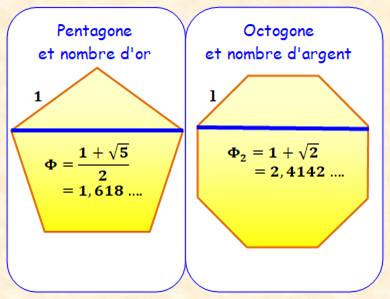
Voir Pentagone / Octogone  / Brève 563

 

SUITE de LUCAS {1, 3 / 1, 1}

 

Somme comme Fibonacci
Mais, avec 1 et 3
comme points de départ.

L1 = 1

L2 = 3

Ln+2 = Ln+1 + Ln

Remarque: L0 = 2

 

1    3

1 + 3 = 4

      3 + 4 = 7

            4 + 7 = 11

                  7 + 11 = 18

                         11 + 18 = 29

                                  18 + 29 = 47

                                           29 + 47 = 76 …

Nombres de Lucas (en rouge: nombre premiers

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, 15127, 24476, 39603, 64079, 103682, 167761, 271443, 439204, 710647, 1149851, 1860498, 3010349, 4870847, 7881196, 12752043, 20633239, 33385282, 54018521, 87403803, …

A000032

 

Rang des Lucas premiers

0, 2, 4, 5, 7, 8, 11, 13, 16, 17, 19, 31, 37, 41, 47, 53, 61, 71, 79, 113, 313, 353, 503, 613, 617, 863, 1097, 1361, 4787, 4793, 5851, 7741, 8467, 10691, 12251, 13963, 14449, 19469, 35449, 36779, 44507, 51169, 56003, 81671, 89849, 94823, 140057, 148091, 159521, 183089, 193201, 202667, 344293,…

A001606

 

Le rapport entre deux termes consécutifs converge vers le nombre d'or.

Chaque nombre de Lucas est aussi en relation avec le nombre d'or ϕ

*    C'est la somme         Voir tableau ci-dessous

*    C'est aussi  , arrondi à l'entier le plus proche.

 

2-step Lucas

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, 15127, 24476, 39603, ….

OEIS A000204

3-step Lucas

1, 3, 7, 11, 21, 39, 71, 131, 241, 443, 815, 1499, 2757, 5071, 9327, 17155, 31553, 58035, 106743, 196331, 361109, 664183, 1221623,  …

OEIS A001644

4-step Lucas

1, 3, 7, 15, 26, 51, 99, 191, 367, 708, 1365, 2631, 5071, 9775, 18842, 36319, 70007, 134943, 260111, 501380, 966441, 1862875, 3590807, 6921503, …

OEIS A001648

5-step Lucas

1, 3, 7, 15, 31, 57, 113, 223, 439, 863, 1695, 3333, 6553, 12883, 25327, 49791, 97887, 192441, 378329, 743775, 1462223, 2874655, 5651423, 11110405, 21842481, …

OEIS A023424

 

 

Lucas et somme avec nombre d'or (Phi)

Voir Nombre d'or / Formule de Binet / Puissance du nombre d'or

 

Puissances du nombre d'or, Fibonacci et Lucas

  

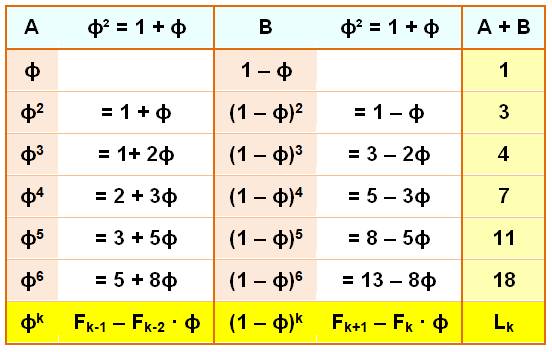
Voir Brève 792

 

Pseudo-premier de Fibonacci (à partir des nombres de Lucas)

 

Définition 1

Nombre pseudo-premier de Fibonacci ou pseudo-premier de Bruckman-Lucas.

Il s'agit d'un nombre composé (impair) de Lucas d'ordre n (Ln) qui est congru à 1 modulo :


Liste:  705, 2465, 2737, 3745, 4181, 5777, 6721, 10877, 13201, 15251, 24465, 29281, 34561, 35785, 51841, 54705, 64079, 64681, 67861, 68251, 75077, 80189, 90061, 96049, 97921, 100065, 100127, 105281, 113573, 118441, 146611, 161027,  … OEIS A005845

 

Définition 2

Nombre pseudo-premier IMPAIR de Fibonacci

Nombre composé impair k tels que soit:

*      k divise F(k – 1) si k = 1 ou -1 mod 5, ou

*      k divise F(k + 1) si k = 2 ou -2 mod 5.

 

Liste: 323, 377, 1891, 3827, 4181, 5777, 6601, 6721, 8149, 10877, 11663, 13201, 13981, 15251, 17119, 17711, 18407, 19043, 23407, 25877, 27323, 30889, 34561, 34943, 35207, 39203, 40501, 50183, 51841, 51983, 52701, 53663, 60377, 64079, 64681, … OEIS A081264

 

 

Définition 3 (même définition, mais avec des nombres pairs)

Nombre pseudo-premier PAIR de Fibonacci

Nombre composé impair k tels que soit:

*      k divise F(k – 1) si k = 1 ou -1 mod 5, ou

*      k divise F(k + 1) si k = 2 ou -2 mod 5.

 

Liste: 8539786, 12813274, 17340938, 33940178, 64132426, 89733106, 95173786, 187473826, 203211098, 234735586, 353686906, 799171066, … OEIS A141137

   

 

 

 

SUITE de PELL {0, 1 / 1, 2} – Nombres de Pell

 

*      Somme de deux fois le précédent et une fois l'autre d'avant;

Avec 0 et 1 pour points de départ.

 

 

*      Cette suite donne les dénominateurs des réduites de racine de 2

 

 

0    1

0 + 2 = 2

      1 + 4 = 5

           2 + 10 = 12

                  5 +  24 = 29

                          12 + 58 = 70

                                  29 + 140 = 169

                                            70 + 338 = 408

 

… 985, 2378, 5741, 13860, 33461, 80782, 195025, 470832, 1136689, 2744210, 6625109, 15994428, 38613965, 93222358, 225058681, 543339720, 1311738121, 3166815962, 7645370045, 18457556052, 44560482149, 107578520350, 259717522849 …

 

*      Le rapport entre deux termes consécutifs converge vers le nombre d'argent ou proportion d'argent.

Anglais: Pell numbers or lambda numbers

Voir Équation de Pell / Nombres de Markov

Merci à Nicolas pour ses remarques

 

SUITE de PELL – LUCAS {1, 2 / 1, 2} ou {2, 2 / 1, 2}

 

*      Somme de deux fois le précédent et une fois l'autre d'avant.

Avec 1 et 2 pour points de départ.

 

 

 

1     2

1  + 4 =   5

       2 + 10 = 12

                5 + 24 = 29

                     12 +  58 = 70

                               29 + 140 = 169

 

… 408, 985, 2378, 5741, 13860, 33461, 80782, 195025, 470832, 1136689, 2744210, 6625109, 15994428, 38613965, 93222358, 225058681, 543339720, 1311738121, 3166815962, 7645370045, 18457556052, 44560482149, 107578520350, 259717522849, 627013566048, 1513744654945, 3654502875938, 8822750406821 …

 

*      Le rapport entre deux termes consécutifs converge vers le nombre d'argent.

 

*      Idem avec départ à 2 et 2.

*      Le rapport converge également vers 1 + racine de 2

 

 

2     2

2  + 4 =   6

       2 + 12 = 14

                6 + 28 = 34

                     14 +  68 = 82

                               34 + 164 = 198

 

… 198, 478, 1154, 2786, 6726, 16238, 39202, 94642, 228486, 551614, 1331714, 3215042, 7761798, 18738638, 45239074, 109216786, 263672646, 636562078, 1536796802, 3710155682, 8957108166, 21624372014, 52205852194, 126036076402, 304278004998…

 

Anglais: Companion Pell numbers

 

 SUITE de FIBONACCI généralisée {A, B / R, S}

 

*      Suite de nombres telle que:

 

U1 = A 

U2 = B 

Un = R.Un-1 + S.Un-2

 

avec A, B, R, S des réels donnés

 

 

*      Avec A = B  = R = S = 1
Nous avons la suite de Fibonacci dont le rapport de deux termes consécutifs converge vers le nombre d'or

 

 

*      Quelles que soient les valeurs de A et de B, le rapport de deux termes consécutifs converge vers une valeur cousine du nombre d'or donné par cette formule:

 

 

 

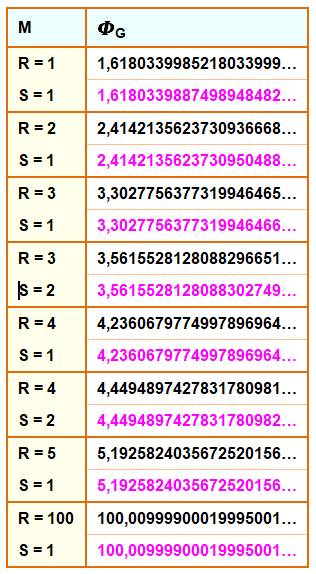
Exemples

 

Quelques valeurs en fonction de R et S.

*    En voir la valeur calculée par le rapport entre deux nombres successifs après vingt itérations.

*    En rose, la valeur calculée avec la formule.

 

On retrouve la valeur du nombre d'or et celle du nombre d'argent dans les deux premiers cas.

 

Naturellement pour R grand devant S, la valeur de Phi généralisé se rapproche de celle de R.

 

 

Voir Développements sur ces suites / Calcul de ces suites

 

 

 LUCAS & FIBONACCI


 

Définitions

 

Fibonacci

Lucas

F(n+2) = F(n+1) + F(n)

avec F(1) = F(2) = 1

L(n+2) = L(n+1) + L(n)

avec L(1) = 1 and L(2) = 3

  

 Liste

 

N

1

2

3

4

5

6

7

8

9

10

11

12

Fibonacci

1

1

2

3

5

8

13

21

34

55

89

144

Lucas

1

3

4

7

11

18

29

47

76

123

199

322

 

13

14

15

16

17

18

19

20

21

 

233

377

610

987

1597

2584

4181

6765

10946

...

521

843

1364

2207

3571

5778

9349

15127

24476

...

 

  

Relations

 (extrait du tableau ci-dessus)

F(n+1) + F(n-1) = L(n)

L(n+1) + L(n-1) = F(n)*5

21 + 8 = 29

47 + 18 = 65 = 13 x 5

6

7

8

6

7

8

8

13

21

8

13

21

18

29

47

18

29

47

  

F(2n) = F(n) * L(n)

21 = 3 x 7

4

5

6

7

8

3

5

8

13

21

7

11

18

29

47

  

Autres relations

 

L(n)2  

F(n+1)*F(n–1) – F(n)2  

L(n+1)*L(n–1) – L(n)2  

Pair: F(2n+1)  

Impair : F(2n) 

F(n+p+1)   )

Somme [F(k) avec (k = 1 à n)]  

Somme [L(k) avec (k = 1 à n)]  

=   5F(n)2 + 4(–1)n 

=   (–1)n   

=   5*(–1)n+1    

=   F(n+1)2 + F(n)2 

=   F(n+1)2 – F(n–1)2  

=   F(n)*F(p) + F(n+1)*F(p+1)

=   F(n+2) – 1

=   L(n+2) – 3

 

 

Fibonacci premiers

 

Fn est premier si n est premier ou si n = 4.

Condition nécessaire, mais  pas suffisante; voir le cas 19.

 

n = P

2

3

5

7

11

13

17

19

 

Fn

1

2

5

13

89

233

1597

4181

...

 

P*

P

P

P

P

P

P

37 x 113

 

 * par extension et générosité

 

 

Liste des valeurs de n pour lesquelles Fn est premier

 

3

4

5

7

11

13

17

23

29

43

47

83

131

137

359

431

433

449

509

569

571

2971

4723

5387

9311

 

 

 

 

Les N-bonacci

Les nombres de Fibonacci généralisés, les N-bonacci, sont liés à la quantité de partition des nombres selon les nombres utilisés pour effectuer la partition.

*    Fibonacci: 1,  2

*    Tribonacci: 1, 2 et 3

*    Tétranacci: 1, 2, 3 et 4

*    Etc.

 Exemple pour le nombre 6:

*      F6 = 13 et il y a 13 partitions de 6 avec les nombrees1 et 2;

*      Tri6 = 24 et il y a 24 partitions de 6 avec les nombrees1, 2 et 3;

*      Tét6 = 29 et il y a 29 partitions de 6 avec les nombrees1, 2, 3 et 4;

Voir Partitions et escaliers

 

  

 TRIBONACCI

 

*    Somme des trois nombres précédents

 

1

1

2

4

7

13

24

44

81

149

274

Etc.

 

Les 25 premiers tribonacci

1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, 410744, 755476, 1389537, 2555757, 4700770, 8646064, 15902591, 29249425, 53798080, 98950096, 181997601, 334745777, 615693474, 1132436852, 2082876103, 3831006429, 7046319384, 12960201916, 23837527729, 43844049029, 80641778674, 148323355432, 272809183135, 501774317241, 922906855808, 1697490356184, 3122171529233, 5742568741225, 10562230626642, 19426970897100, 35731770264967 …

 

*    Si r1, r2 et r3 sont les racines de x3 – x2 – x – 1, alors les nombres de tribonacci sont une combinaison linéaire de leur puissance énième.

*    La racine réelle est la constante de tribonacci (t) qui se trouve également être la limite du quotient de deux termes consécutifs.

 

t = r1 = 1, 839 286 755 214 161 132 1…

 

*    Les deux racines complexes, conjuguées l'une de l'autre et de module inférieur à 1 sont appelées les nombres de tribonacci.

 

r2 = – 0, 41964337760708056629 + i  0, 60629072920719936925

r3 = – 0, 41964337760708056629 – i  0, 60629072920719936925

 

 

*    Constante de tribonacci

 

= 2

= 2

 

 

*    Cas de la première identité: comment en arrive-t-on à 2?

 

 

 

*    On démontre que Tn+1 est le nombre de façons de découper un saucisson de longueur n en tranches dont l'épaisseur peut varier entre 1, 2 ou 3.

 

Voir Nombre 1,939…  / Nombre 2

 

 

Généralisation

Les nombres tétranacci commencent par 0, 0, 0, 1 et se poursuivent en ajoutant les quatre termes précédents:

1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, 76424, 147312, 283953, 547337, 1055026, 2033628, 3919944, 7555935, 14564533, 28074040, 54114452, 104308960, 201061985, 387559437, 747044834, 1439975216, 2775641472 …

 

Les nombres pentanacci:

1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, 26784, 52656, 103519, 203513, 400096, 786568, 1546352, 3040048, 5976577, 11749641, 23099186, 45411804, 89277256, 175514464, 345052351, 678355061, 1333610936, 2621810068 …

 

Liste de tous les nombres de Fibonacci à pentanacci

1, 2, 3, 4, 5, 7, 8, 13, 15, 16, 21, 24, 29, 31, 34, 44, 55, 56, 61, 81, 89, 108, 120, 144, 149, 208, 233, 236, 274, 377, 401, 464, 504, 610, 773, 912, 927, 987, 1490, 1597, 1705, 1793, 2584, 2872, 3136, 3525, 4181, 5536, 5768, 6765, 6930, 10609, 10671, 10946, 13624, 19513, 20569, 26784, 35890, 39648, 52656, 66012, 76424, 103519, 121415, 147312, 203513, 283953, 400096 …

Voir Tables de ces nombres et leur primalité

 

 

 

Fibonacci en puissance

 

Recherche sur les nombres de Fibonacci

 

Quels sont ceux qui sont carrés, cubes …

Dont la somme est un carré …

 

Fibonacci carré

Rang

2

3

13

< 1000

Fn

1

1

144

Aucun autre

 

Fibonacci cube

Rang

2

3

7

< 100

Fn

1

1

8

Aucun autre

 

Fibonacci puissance 5

Rang

2

3

< 100

Fn

1

1

Aucun autre

 

Somme de 2 Fibonacci consécutifs = carré

Rang

11

< 100

Fn

55

Aucun autre

Fn+1

89

 

Somme de 2 Fibonacci consécutifs = cube

Rang

5

< 100

Fn

3

Aucun autre

Fn+1

5

   

 

 

Somme rationnelle

 

Principe de sommation

 

On peut former une addition spéciale avec les nombres de Fibonacci.

 

En décalant chaque nombre d'un cran vers la droite.

 

 

Suite de cette somme (tableur) >>>

 

 

Résultats

 

 

*       La limite de cette somme avec les Fibonacci est exactement 10/89, qui est un nombre rationnel, périodique qui se répète après 44 décimales.

10 / 89   =   0,112 359  …

 

= 0, 112 359 550 561 797 752 808 988 764 044 943 820 224 719 10  112 359 5 …

 

*       Suite des 25 premiers termes de Fibonacci:

 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025
          

 

Valeur de la somme décalée

 

 

0, 112 359 550 561 797 752 807 540 5

 

*       La même propriété se retrouve avec les nombres de Lucas

Rationnel de période 44 (comme ci-dessus)

12 / 89   =   0,134 831  …

 

= 0, 134 831 460 674 157 303 370 786 516 853 932 584 269 662 92  134 831 4 …

 

*       Suite des 25 premiers termes de Lucas:

 

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, 15127, 24476, 39603, 64079, 103682, 167761
 

 

Valeur de la somme décalée

 

0, 134 831 460 674 157 303 367 548 1

 

*       En décalant les Fibonacci de deux crans.
 

10 /     9 899 = 0,010 102 030 508 …

 

*       Avec trois crans.

10 / 998 999 = 0,000 010 020 030 …

*       Etc.

…

 

Quel est le phénomène qui pousse ces sommes à tendre

vers des nombres rationnels lorsqu'on va jusqu'à l'infini ?

L'explication par les polynômes générateurs >>>

 

 

Suite en Pourquoi 1/89 / Voir Nombres périodiques

 

 

 

 

 

Suite

*       Suite de Padovan

*       Tables de ces nombres

Voir

*       Boucle infernale en carrés

*       Calcul mental – Index

*       Chaîne d'Or

*       Fraction continue

*       Géométrie – Index

*       Nombre d'or

*       Nombres en cercle

*       Récurrence

*       Théorie des nombres

Sites

*       Tribonacci numbers – Wolfram

*       OEIS A000129 – Pell numbers

*       OEIS A000204 – Lucas numbers

*       OEIS A002203 – Companion Pell numbers

*       OEIS A000073 – Tribonacci numbers

*       OEIS A000078 – Tretranacci numbers

*       OEIS A001591 – Pentanacci numbers

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Iteration/FiboLuca.htm