|
||||||||||||||||||||||||||||||||||||||||
![]()
|
PRINCIPE
MULTIPLICATIF THÉORÈME FONDAMENTAL DU DÉNOMBREMENT Une règle qui semble évidente mais, qu'il faut bien
posséder. Elle est utilisée en permanence dans les problèmes de
dénombrement. Illustration
|
Anglais:
Fundamental principle of counting
Possibilités
= ways (in how many ways the operation can be performed ?)
Pas de chance!
|
Humour Deux
garçons se présentent en retard pour l'examen de physique. Ils expliquent
que, pas de chance, ils ont eu une crevaison. Magnanime, le professeur reporte
l'épreuve au lendemain. Les deux garçons sont placés dans deux salles
différentes et découvrent l'énoncé: Indiquez-moi quelle roue? Au-delà de la blague, on peut estimer la
probabilité d'une bonne réponse Quelle est la probabilité de donner la même réponse:
l'histoire étant imaginaire, le premier va répondre n'importe quoi; disons la
roue avant-gauche. Le second va proposer l'une des quatre. Soit le calcul de
probabilité: quatre cas possibles pour un seul cas favorable. La probabilité
est 1/4. Par contre, imaginons une voiture avec une réelle
crevaison. Le premier a une chance sur 4 de deviner laquelle et même chose
pour le second. Les deux choix étant indépendants, les probabilités se
multiplient; Soit la probabilité que les deux garçons détectent tous les deux
la roue crevée est égale à 1/16. On peut aussi compliquer le sujet en imaginant
plusieurs crevaisons … |
|
|
||||
|
Trois choix à faire successivement
(on parle d'événements):
Ces trois événements A, B et C sont
indépendants les uns des autres. Le total des possibilités n est le
produit des possibilités de chaque événement. n = a . b . c = 1000 |
|||
|
|
|||
|
Si un
événement A peut se produire de a façons, un
événement B peut se produire de b façons, un
événement C peut se produire de c façons, … Et Tous
ces événements étant indépendants, Alors Le total n des
possibilités de l'événement
combiné A, B, C, … est le produit des possibilités de chaque
événement. |
Théorème fondamental
du dénombrement ou principe
multiplicatif ou principe du produit
Ce principe s'applique lorsque les possibilités offertes s'enchaînent
les unes à la suite des autres pour créer l'événement complet. Il y a
possibilité de choix, puis à ce niveau se présente encore une possibilité de
choix, etc. |
||
|
Une
cravate propre attire la soupe du jour. Une
cravate propre attire inévitablement les aliments. Et l'aliment qui tombe est
toujours celui dont la tache est indélébile. |
Voir Loi de Murphy
/ Pensées & humour
|
|
||
|
Il a 5 chemises et 3 cravates. Combien de choix, le matin en
s'habillant ? Il a 5 x 3 choix. |
Ayant choisi une chemise, il a le
choix entre 3 cravates; Et ce, pour chacune des 5 chemises. Soit 5 x 3 possibilités. Équivalent
à un compteur à
deux molettes l'un allant jusqu'à 5 et l'autre jusqu'à 3; soit 15
possibilités. |
|
Le saviez-vous? Combien de nœuds de cravate?
|
Il
y en a 85 selon les mathématiciens de l'Université de Cambridge (2000). Mais,
beaucoup plus: 177 147 selon l'Institut royal de technologie de Stockholm
(2014). L'équipe
anglaise s'était limitée aux nœuds raisonnables. L'autre équipe a fait une
recherche exhaustive. Leur recherche se serait produite suite à la découverte
d'un nœud non inclus dans la série des 85, fait découvert à l'occasion du
film The Matrix Reloaded. Pour effectuer ce calcul, l'équipe s'est limitée à
onze pliages (huit pour l'équipe aux 85), estimant qu'au-delà la cravate
deviendrait trop courte pour supporter le nœud. Et alors si, on prenait des
cravates illimitées en longueur ? We
extend the existing enumeration of neck tie knots
to include tie knots with a textured front, tied with the narrow end of a
tie. These tie knots have gained popularity in recent years, based on
reconstructions of a costume detail from The Matrix Reloaded, and are
explicitly ruled out in the enumeration by Fink and Mao (2000). Read more at >>> |
Voir DicoNombre
177 147 / Théorie des nœuds
|
|
||
|
Cette salle dispose de 3 portes
d'entrées et de 2 de sorties. Combien de chemins d'entrées /
sorties ? Il y a 3 x 2 = 6 chemins. |
Pour chaque porte d'entrée, il y 2
chemins de sortie. Soit 3 fois 2 chemins. Équivalent
à un compteur à
deux molettes l'un allant jusqu'à 3 et l'autre jusqu'à 2; soit 6
possibilités. |
|
|
|
||
|
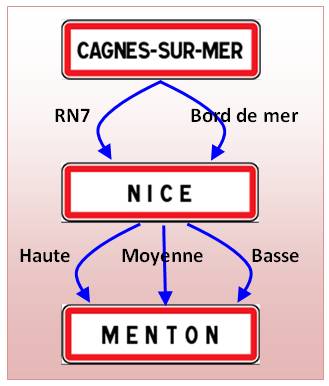
Il y a trois routes pour aller de
Nice à Monaco:
Combien de
possibilités. Il y a 3 x 3 = 9 chemins. |
Pour chacune des trois possibilités à
l'aller, il y a trois possibilités pour le retour. Soit 3 x 3 chemins. Équivalent
à un compteur à
deux molettes l'un allant jusqu'à 3 et l'autre jusqu'à 3; soit 9
possibilités. |
|
|
|
||
|
Une classe de 15 garçons et 12 filles Il faut un garçon et une fille pour
représenter la classe. Combien de possibilités de choix ? Il y a 15 x 12 = 180 possibilités. |
15 possibilités pour choisir un
garçon, et 12 possibilités pour choisir la
fille. Équivalent
à un compteur à
deux molettes l'un allant jusqu'à 15 et l'autre jusqu'à 12; soit 180
possibilités. |
|
|
|
||
|
Trois élèves se présentent en
classe, alors qu'il reste 6 chaises libres. Combien de possibilités de choix ? Il y a 6 x 5 x 4 = 120 possibilités. |
Le premier a 6 possibilités; il ne
reste plus que 5 chaises. Le deuxième a 5 possibilités; il ne
reste plus que 4 chaises. Le troisième a 4 possibilités. Équivalent
à un compteur à
trois molettes l'un allant jusqu'à 6, le suivant jusqu'à 5 et le dernier
jusqu'à 4; soit 120 possibilités. |
|
|
|
||
|
L'association de 20 membres souhaite
élire:
Combien y-a-t-il de possibilités d'avoir ces
trois responsables. Pas de cumul de fonction. Il y a 20 x 19 x 18 = 36 342
possibilités. |
L'événement A = le président existe
avec a = 20 possibilités (20 membres). L'événement B = le secrétaire existe
avec b = 19 possibilités (19 membres restants). L'événement C = le trésorier existe avec
c = 18 possibilités (18 membres restants). Ces trois événements A, B et C sont
indépendants Le total des possibilités n est le
produit des possibilités de chaque événement n = 20 .
19 . 18 =
36 342 |
|
|
|
||
|
La plaque d'immatriculation des voitures comportait:
Combien y-a-t-il de possibilités
pour un département donné? Il y a 9 999 x 24 x 24 = 5 759 424
possibilités. |
L'événement A = les nombres de 1 à
9999: a = 9999 possibilités. L'événement B = la première lettre: b
= 26-2 possibilités. L'événement C = la deuxième lettre: c
= 26-2 possibilités. Ces trois événements A, B et C sont indépendants.
Le total des possibilités n est le produit des possibilités de chaque
événement n = a . b . c = 5 759 424 Il est donc possible d'immatriculer
plus de 5 millions de voitures par département. Avec une lettre de plus, on aurait
24 fois plus de possibilités, soit plus de 100 millions, nombre plus grand
que la population
française. |
|
|
|
|||
|
Soit n(A) le cardinal
de A, la quantité d'éléments de l'ensemble
A. |
Règle multiplicative Si A x B
est le produit cartésien des ensembles A et B:
|
||
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()