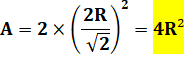|
||||||||||||||||||||||||||||
![]()
|
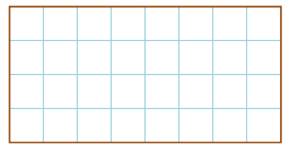
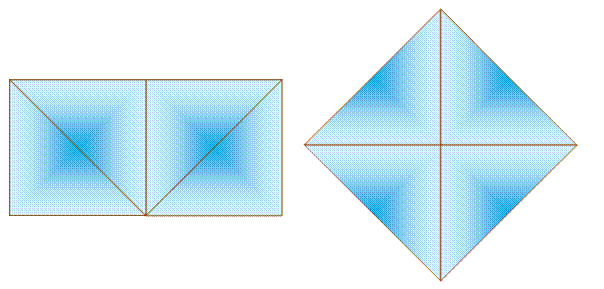
Découpez ce rectangle pour former un carré
|
|
|
|
|
En quatre coups de ciseau
faire de ce rectangle (20 x 8) un carré.
|
|
Voir Solution
|
|
||
|
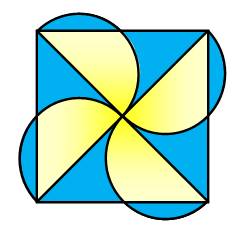
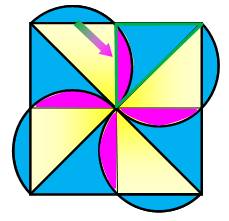
Quelle est l'aire de la zone
colorée en bleu en fonction de R le rayon des demi-cercles ? |
|
|
Voir Solution
![]()
|
|
|
|
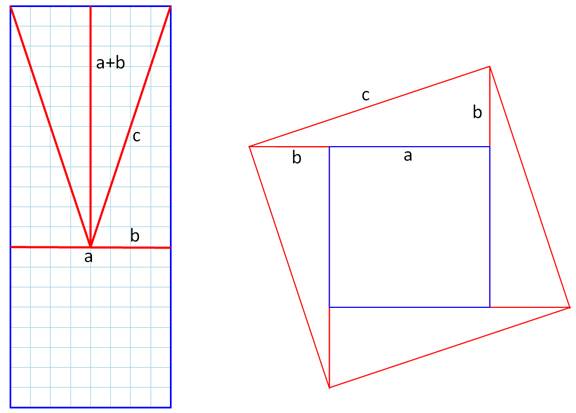
Conserver le carré et
découpez quatre triangles
rectangles identiques.
Condition: On note bien que le carré de
c (c² = 160) est bien l'aire du
rectangle initial (20 x 8 = 160). |
|
Retour Énoncé / Voir Démonstration du théorème de
Pythagore
|
|
||
|
En plaçant les segments de cercles
(bleus) qui dépassent dans le carré (en mauve), on forme le triangle vert, en
fait, un demi-carré de diagonale 2R. L'aire cherchée correspond
donc à quatre tels triangles ou 2 petits carrés.
Remarque: la diagonale du grand carré mesure 4R. Pour un rayon unité, l'aire de la zone bleue vaut 4 comme la mesure de
la grande diagonale. |
|
|
|
Découpez le rectangle pour former un carré.
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()