|
||||||||||||||||||||||||||||||||
![]()
|
|
|
||
|
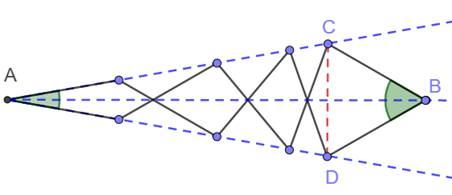
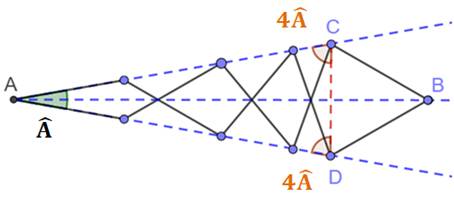
Un
tirebouchon comprend ces 10 bras articulés, chacun de la même taille. Avec cet
alignement et le fait que l'angle en B vaut 60°, déterminer la valeur de
l'angle en A. |
|
|
Note: Le tirebouchon habituel est plutôt constitué de
losanges articulés
|
|
||
|
Analyse des
angles dans les triangles isocèles à partir du sommet A jusqu'au sommet B. |
||
|
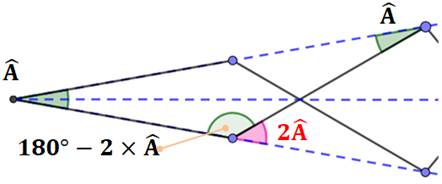
Sur cette
extrait, dans le triangle isocèle, les angles à la base sont égaux (A). L'angle au
sommet est calculé sachant que la somme des angles vaut 180°. On en
déduit la valeur de l'angle rose: 180 – (180 – 2A) = 2A. |
|
|
|
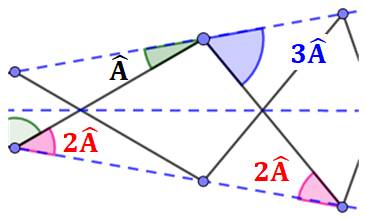
Dans le triangle
isocèle, les angles à la base valent 2A. |
|
|
|
Dans le
triangle isocèle, les angles à la base valent 3A. L'angle
marron se calcule: |
|
|
|
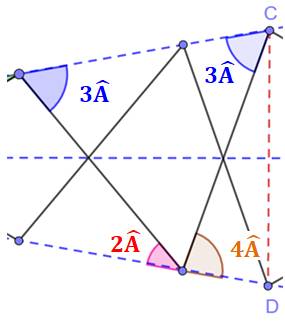
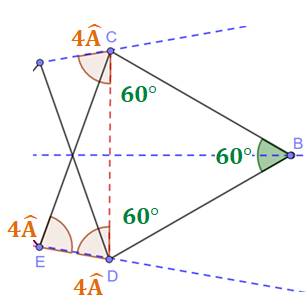
Triangle
CBD: deux côté égaux et un angle de 60°, il est équilatéral et CD = BC= BD. Le
triangle DCE est isocèle. Ses angles à la base valent 4A. Par symétrie,
l'angle en C vaut également 4A. |
|
|
|
Dans le
triangle isocèle ACD, la somme des angles vaut 180°: A = 20° Les figures respectent les angles. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()