|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres devinés suite à une conversation Deux puzzles de déduction: deviner
le nombre de l'autre suite à un dialogue entre ces deux personnes. Énigmes supposées simples. Ouais ! À
condition de les prendre par le bon bout. Explication détaillée en images. |
|
|
||
|
Énigme Deux nombres consécutifs
sont confiés à deux personnes, chacun le sien. Une conversation se tient pour savoir si l'un ou
l'autre à deviné le nombre de son voisin. Pouvez-vous en déduire l'unique nombre donné à
l'un ou à l'autre ? |
Conversation Premier tour Adam: j'avoue que je
ne peux vraiment rien dire. Éve: c'est la même
chose pour moi. Second tour Adam: et bien dans
ce cas, moi je sais dire des choses. Ève: moi aussi, je
connais ton nombre. |
|
|
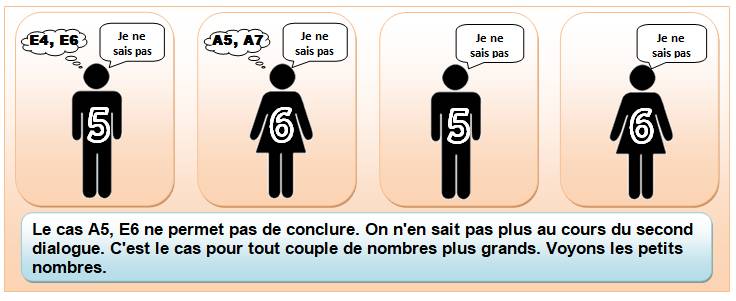
Principe de la solution Si, par exemple, les deux nombres sont 5 pour
Adam et 6 pour Ève, aucun moyen de deviner le nombre de l'autre. Alors, ce
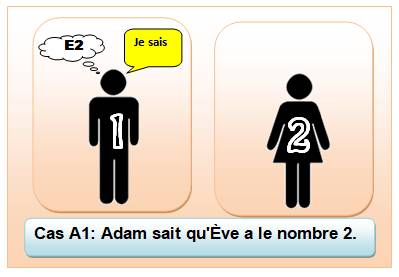
dialogue est impossible ! Voyons tout de même les petites valeurs. Si Adam a le 1, il devine immédiatement qu'Éve a
le 2 et en annonçant qu'il sait, Ève sait également. Nous tenons une piste ! |
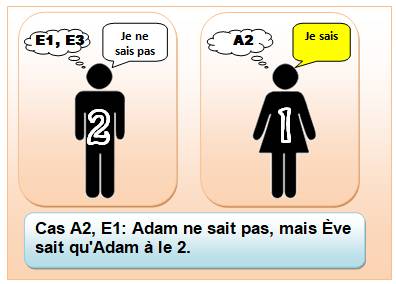
Commentaires On note A2 lorsqu'Adam a le nombre 2 et E3 si Ève
dispose du nombre 3. Examinons le cas des nombres 1, 2, 3 et 4. L'illustration montre trois informations par
personnage:
|
|
Examen
illustré des cas
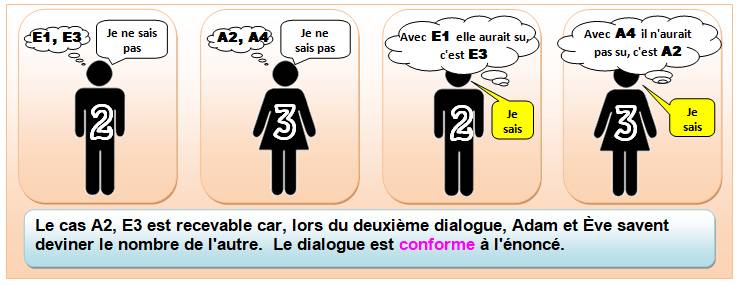
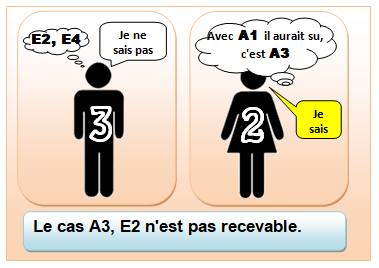
Avec son 2, si Adam pense qu'Ève a le 1, alors elle répondrait
qu'elle sait (voir le cas précédent).
Si elle ne sait pas, c'est que c'est l'autre possibilité,
le 3.
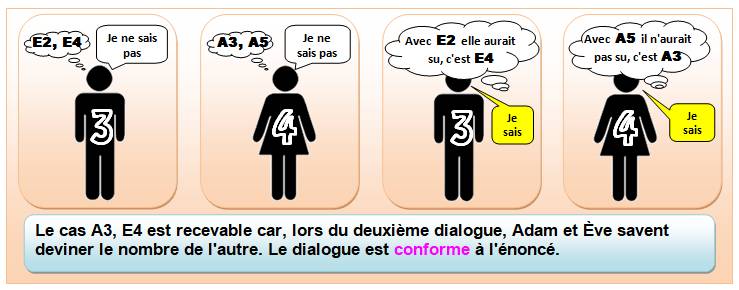
Avec son 3, si Adam pense qu'Ève a le 2, alors elle répondrait
qu'elle sait (voir le cas précédent).
Si elle ne sait pas, c'est que c'est l'autre possibilité
le 4.
Bilan
|
Deux cas recevables: (A2, E3) et (A3,
B4). L'unique nombre confié à l'un ou à
l'autre est le 3. |
![]()
|
|
||
|
Énigme Deux nombres consécutifs
compris entre 1 et 10 sont confiés à deux
personnes, chacun le sien. Une conversation se tient pour savoir si l'un ou
l'autre à deviné le nombre de son voisin. Pouvez-vous en déduire les quatre paires de
nombres possibles? |
Conversation A: j'avoue que je ne peux vraiment rien dire. E: c'est la même chose pour moi. A: et bien dans ce cas, moi je sais dire des
choses. |
|
|
Principe de la solution D'évidence les nombres ne sont pas 1 et 10, sinon
le nombre de l'autre serait deviné immédiatement. |
Commentaires Comme précédemment, on identifie deux solutions (2, 3) et (3, 4). Voir rappel en tableau ci-dessous. Dans cette énigme, les nombres sont limités à 10.
On peut donc conduire le raisonnement en partant de 10 au lieu de 1 et
identifier deux autre solutions: (9, 8) et (8,
7). |
|
|
Cas |
A |
E |
A |
OK ? |
|
A1, B2 |
A sait que B2 |
/ |
|
non |
|
A2, B1 |
A ne sait pas si 1 ou 3 |
mais E sait que A2 |
/ |
non |
|
A2, B3 |
A ne sait pas si 1 ou 3 |
B ne sait pas si 2 ou 4 |
Si B ne sait pas, ce n'est pas le cas
A2, B1; c'est B3 |
OUI |
|
A3, B2 |
A ne sait pas si 2 ou 4 |
B sait que ce n'est pas A1, il déduit que c'est A3 |
/ |
non |
|
A3, B4 |
A ne sait pas si 2 ou 4 |
B sait ne sait pas si c'est A3 ou A5 |
Si B ne sait pas, ce n'est pas le cas
A3, B2; c'est B4 |
OUI |
|
A4, B3 |
A ne sait pas si 3 ou 5 |
B sait ne sait pas si c'est A2 ou A4 |
A ne sait rien dire de plus |
non |
Anglais
|
A teacher thinks of two consecutive
numbers between 1 and 10. The first student knows one number and the second
student knows the second number. The following exchange takes place:
What are the four solutions of this
easy number puzzle? |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
