NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/01/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	JEUX
Débutants Général	ÉNIGMES				Glossaire Général
INDEX JEUX	Classiques	Famille	Graphes	Villa
	Chapeaux	Truel	Chasseur	Pastis
	Nombres de 1 à 10
		Sommaire de cette page >>> Les points sur le front >>> Chapeaux et pièces de monnaie >>> Chapeaux de couleur >>> Chapeaux au vestiaire

Problèmes avec des CHAPEAUX

Casse-tête classiques qui stimulent l'esprit de déduction.

Devinette

Trois personnes sortent du restaurant un peu éméchés. Ils reprennent leur chapeau au hasard. Quelle est la probabilité que deux seulement aient pris leur chapeau ?

Solution

Pour se mettre en jambe, une énigme classique
Deux prisonniers avec un point blanc ou un point noir sur le front. Au moins, l'un des deux points est blanc. Celui qui devine la couleur de son point est gracié et l'autre condamné.	Cas d'un prisonnier un peu neuneu Il est le premier à parler et finalement passe son tour. Ayant vu le blanc sur le front de son collège, il ne peut rien déduire. Son collègue fait la même déduction et conclut qu'il a le blanc. Il est gracié. Cas d'un prisonnier un peu plus malin Il s'empresse de prendre la parole le premier pour dire qu'il passe. Le second en conclut comme précédemment qu'il porte le point blanc. En fait, le premier a passé alors qu'il y avait un point noir sur le front de son collègue. Cette entourloupe lui a valu la vie sauve.

1) CHAPEAUX & PIÈCES – Problème
Dix chapeaux et dix pièces de monnaie dans chaque chapeau. Ces pièces pèsent toutes 10 grammes sauf celle d'un des chapeaux qui ne pèsent que 9 grammes. En une seule pesée trouver le chapeau singulier.

Solution

2) CHAPEAUX DE COULEUR – Problème
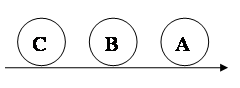
Trois personnes A, B et C en file indienne. Chacun regardant droit devant. Quatre chapeaux: deux bleus et deux rouges. Yeux bandés, on pose un chapeau au hasard sur chaque tête. On demande à chacun de deviner la couleur de son chapeau. Long silence ! Et, finalement, c'est B qui annonce la couleur de son chapeau. Comment le sait-il ?

Solution

2bis) CHAPEAUX (variante) – Problème
Trois personnes A, B et C ont les yeux bandés. Parmi 3 chapeaux blancs et 2 chapeaux noirs, chacun en reçoit un. On enlève les bandeaux, mais étant l'un derrière l'autre, C voit A et B, B voit A et A ne voit rien. Ils gagnent si au bout d'une minute l'un d'eux sait quel chapeau il porte. À la 59^e seconde, A dit, je sais. Quelle est la couleur du chapeau? Pourquoi?

Anglais: 3 Heads & 5 Hats Puzzle

Solution

2ter) CHAPEAUX (variante) – Problème

Trois personnes A, B et C ont les yeux bandés. Parmi 3 chapeaux blancs et 2 chapeaux noirs, chacun en reçoit un. On enlève les bandeaux, chacun voit les deux autres. Ils gagnent si au bout d'une minute l'un d'eux sait quel chapeau il porte. À la 59^e seconde, A dit, je sais. Quelle est la couleur du chapeau? Pourquoi? Variantes avec une pastille noire ou blanche accrochée dans le dos des personnes ou un disque rouge et un disque noir, etc. De sorte que chacun voit le dos des deux autres, mais pas le sien.

Solution

3) CHAPEAUX au VESTIAIRE – Problème
Dix hommes ont laissé leur chapeau au vestiaire. En reprenant un chapeau au hasard, quelle est la probabilité qu'une personne tombe sur son propre chapeau?

Solution

1) CHAPEAUX & PIÈCES – Solution
On prend une pièce du premier chapeau, deux du deuxième, etc. Soit 1+2+3+4+5+6+7+8+9+10= 55 pièces. Toutes identiques, elles pèseraient 550 grammes. La différence avec la pesée réelle donne le rang du chapeau singulier. Exemple La pesée donne: 546 g => 550 – 546 = 4 Ce qui signifie qu'il y a quatre pièces moins lourdes. Les pièces de 9 g sont dans le chapeau de rang 4 .

Retour

2) CHAPEAUX DE COULEUR – Solution
A	Ne voit rien et ne peut rien en déduire.
C	C voit à la fois A et B. Il voit deux chapeaux. Deux hypothèses:
C1	Hypothèse 1 C voit deux chapeaux de la même couleur. Il reste deux chapeaux de l'autre couleur. Son chapeau est de cette autre couleur. Il pourrait annoncer cette nouvelle. Or il reste silencieux. Hypothèse non retenue.
C2	Hypothèse 2 C voit un bleu et un rouge. Il reste un bleu et un rouge pour lui: il ne peut rien en déduire. C'est pourquoi il reste silencieux.
=>	Suite du raisonnement A et B ont donc des chapeaux de couleurs différentes.
B	B effectue le même raisonnement. C étant silencieux, il sait que A et lui ont des chapeaux de couleurs différentes.
=>	Voyant le chapeau bleu de A, B annonce la couleur de son chapeau: rouge
==>	A, ayant suivi mentalement le raisonnement, donne également la couleur de son chapeau: bleu
?	La couleur du chapeau de C reste inconnue Pas de chance pour celui qui en voit le plus.

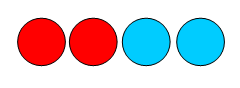
Les 6 cas possibles pour confirmation

Cas	C	B	A
	A et B sont rouges => Je suis bleu	C parle => A et B ont même couleur. Or A est rouge => Je suis rouge	C parle => A et B ont même couleur Or B est rouge => Je suis rouge
	Raisonnement identique Je suis rouge	Je suis bleu	Je suis bleu
	C ne parle pas Je ne sais pas	Ma couleur n'est pas celle de A Je suis rouge	Ma couleur n'est pas celle de B Je suis bleu
	idem	idem	idem
	C ne parle pas Je ne sais pas	Ma couleur n'est pas celle de A Je suis bleu	Ma couleur n'est pas celle de B Je suis rouge
	idem	idem	idem

Retour

2bis) CHAPEAUX Variante – Solution

C voit deux chapeaux et ne dit rien; ils ne sont pas tous deux noirs sinon il dirait qu'il a un blanc. Parmi les deux chapeaux qu'il voit, l'un est blanc: le A ou le B B, constatant que C ne parle pas, fait la même déduction: j'ai un chapeau blanc ou c'est A qu'il l'a. S'il voit A en noir, il sait qu'il a le blanc. Or, il ne dit rien. C'est qu'il ne voit pas A en noir, mais en blanc. A porte un chapeau blanc. English: "A" finally concludes that he is wearing a white hat!

Retour

2ter) CHAPEAUX Variante – Solution
C ne voit pas 2 noirs, sinon il le dirait; il voit soit 2 blancs ou 1 blanc et un noir. Du fait que C n'a pas parlé, si B voyait un rouge, il saurait qu'il est bleu. Or il ne dit rien. Nous sommes dans le cas ou B et A sont blancs tous les deux. A, constatant que ni A ni B ne parlent, fait les mêmes déductions: B et A sont blancs, donc A est blanc.

Retour

3) CHAPEAUX au VESTIAIRE – Solution

Dix hommes ont laissé leur chapeau au vestiaire.

En reprenant un chapeau au hasard, quelle est la probabilité qu'une personne tombe sur son propre chapeau?

Nombre de permutations de 10 chapeaux:	10!	= 3 628 800
Le nombre de mauvaises permutations est l'entier le plus proche de:	10! / e	= 1 334 961
La probabilité de mauvaises permutations est donc:	10! / (10! x e)	= 0,367
Et la probabilité d'une bonne permutation:	1 – 1/e	= 0,632

Apparition de la constante e (exponentielle)

Nombre de chapeaux	Nombre de permutations	Nombre de personnes sans son chapeau	Probabilité que personne n'ait son chapeau
1	1	0	0
2	2	1	0, 5
3	6	2	0, 333 333
4	24	9	0, 375 000
5	120	44	0, 366 666
6	720	265	0, 368 055
7	5 040	1 854	0, 367 857
8	40 320	14 833	0, 367 881
9	362 880	133 496	0, 367 879 1
10	3 628 800	1 334 961	0, 367 879 4
11	39 916 800	14 684 570	0, 367 879 439
12	479 001 600	176 214 841	0, 367 879 441
	Rappel	1/e	0, 367 879 441 2

Voir Dénombrement et e / Énigme des enveloppes

Constante e / Factorielle / Sous-factorielle (dérangement)

Retour

Roman

"I think you're begging the question," said Haydock, "and I can see looming ahead one of those terrible exercises in probability where six men have white hats and six men have black hats and you have to work it out by mathematics how likely it is that the hats will get mixed up and in what proportion. If you start thinking about things like that, you would go round the bend. Let me assure you of that!"

Christie, Agatha - The Mirror Crack'd

Voir Pensées & humour / Roman

Devinette – Solution

Trois personnes sortent du restaurant un peu éméchés. Ils reprennent leur chapeau au hasard. Quelle est la probabilité que deux seulement aient pris leur chapeau ?

Réponse: probabilité nulle car, si deux personnes portent leur propre chapeau, le troisième aussi.

Retour

Suite	Voir haut de page Prix du chapeau et de son ruban
Voir	Dérangements Énigmes des filles Jeux – Index Logique – Index
Cette page	http://villemin.gerard.free.fr/Puzzle/Chapeau.htm