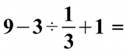|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Problème de la somme et du produit Problème de Freudenthal Précédé du problème de
l'anniversaire de Chloé (ou Cheryl) L'énoncé de ce problème est si
succinct et sibyllin que sa résolution semble impossible. Publié en 1969 par
le néerlandais Hans Freudenthal et baptisé ainsi par Martin Gardner.
La solution n'est pas très simple mais abordable. Il existe diverses versions
de ce problème. >>> Nous allons commencer par un
problème un peu plus simple avant de faire le grand saut: le problème de
l'anniversaire de CHERYL >>>. Ce problème a été posé en 2015 aux enfants (11 ans) des
Singapore and Asian School Math Olympiads. Il a suscité une grande polémique
liée à sa difficulté pour des enfants de cet âge. Voir les autres problèmes
de ce style >>> |
Anglais: Sum and
Product Puzzle or The Impossible Puzzle
Cheryl's Birthday or Albert, Bernard and Cheryl's
birthday maths problem
|
Allemand:
Freudenthal = la vallée des amis |
Voir Contemporains
|
|
||
|
Chloé rencontre deux
nouveaux amis, Alexis et Benoît,
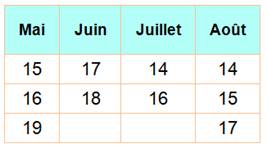
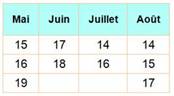
lesquels souhaitent connaître sa date d'anniversaire. Elle donne dix dates possibles:
Et, facétieuse et sans doute
douée en maths, elle donne:
|
Alexis et Benoît tiennent
alors cette conversation: Alexis: Je ne connais
pas la date anniversaire de Chloé, mais je sais que Benoît ne la connait pas
non plus. Benoît: Au début, je n'en savais rien non plus,
mais maintenant, je le sais. Alexis: Alors moi aussi, je le sais. |
|
On trouve aussi cette énigme avec les noms
de Magali, Pierre et Benoît.
|
Indices Seuls les jours 18 et 19 ne
sont pas répétés. Et ces deux jours sont en mai et juin. |
Si Alexis sait que le mois
est juillet ou août, il en déduit que: 1) Benoît peut avoir les jours
de 14 à 17, à l'exclusion de 18 et 19, et 2) Ayant des dates
redondantes, Benoît ne peut pas conclure. |
|
Solution |
|
|
Alexis: Je ne
connais pas la date anniversaire, mais je sais que Benoît ne la connait pas
non plus. Il est évident qu'en ne
connaissant que le mois, je ne peux pas connaitre le jour (il y en a
plusieurs pour chaque mois) |
Si Alexis constate que
Benoît ne peut pas conclure, c'est que le mois est juillet ou août. |
|
|
Benoît: Au début, je n'en savais rien non plus,
mais maintenant, je le sais. Il a tenu le même raisonnement qu'Alexis et sait désormais
que le mois est juillet ou août. S'il sait conclure, c'et que
ce n'est pas le 14 qui figure sur les deux mois. Comme Benoît connait le jour
(15, 16 ou 17), il sait dire le mois. Il sait conclure |
|
Alexis: Alors moi aussi, je le sais. Il a tenu le même
raisonnement que Benoît et déduit qu'il s'agit des 15, 16 ou 17. Or, seul le 16 est sans
ambiguïté. Les 15 et 17 sont dans le même mois. |
Réponse: 16 Juillet Remarque: Nous sommes placés en observateurs sans
connaitre les indications communiquées à Alexis et Benoît. Par contre, eux
les connaissent. Par exemple, à la fin, Alexis sait qu'il s'agit
de juillet et sait qu'il s'agit du 16 sans invoquer la clause de double date
en août. |
|
|
||
|
Problème
|
Conversation Paul: je ne connais pas ces nombres. Sandrine: je m'en doutais bien; mais c'est mon cas
également. Paul: dans ce cas, je sais quels sont les deux
nombres. Sandrine: bravo, mais alors moi aussi. Version originale néerlandaise
|
|
|
|
|
|
|
|
Idée n°1: si Paul ou Sandrine ne peuvent pas répondre, c'est qu'ils font face à
plusieurs solutions. Il y a ambiguïté. Idée n°2: si Paul ou Sandrine peuvent répondre, c'est que chacun a fait le
chemin mental de l'autre. Chacun s'est mis dans le cerveau de l'autre et a
effectué une simulation. |
|
|
|
Version A) Limiter la somme à une petite valeur; Nous
n'abordons pas ce cas; Version B) Nous connaissons les valeurs données à
chacun (17 et 52) et tentons de faire le raisonnement de chacun. >>> Version C) La solution complète sans connaissance
préalable qui impose l'exploration de toutes les possibilités pour les sommes jusqu'à 100. >>> Version D) Sans connaissances préalable, procéder à
une démonstration basée sur la théorie des nombres. La théorie limite
sensiblement l'exploration sans l'annuler. |
|
|
|
||
|
Commentaires
|
Principe du raisonnement
|
|
|
|
||
|
p = m . n = m' . n' |
Exemple: p = 15 Alors p = 3 x 5 de façon unique. Et Paul connait les facteurs m = 3 et n = 5 Exemple: p = 12 Alors p = 2 x 6 = 3 x 4, un produit double. Et Paul et incapable de préciser: (2, 6) ou (3, 4). |
|
|
|
La multiplication est unique si les deux
facteurs sont des nombres
premiers. Paul sera indécis dans tous les autres cas:
soit l'un des facteurs au moins est composé. Loi Paul: Les nombres m et n ne sont pas tous les deux premiers ensembles. |
|
|
|
Loi Sandrine: je dois éliminer toutes les additions de
deux nombres premiers. Exemple: s = 12 = 2 + 10 = 3 + 9 = 4 + 8 = 5 + 7 La paire (5, 7) est à éliminer. |
|
|
D'autant que dans cet
exemple, la loi Sandrine ne permet pas d'éliminer la moindre paire de nombres. |
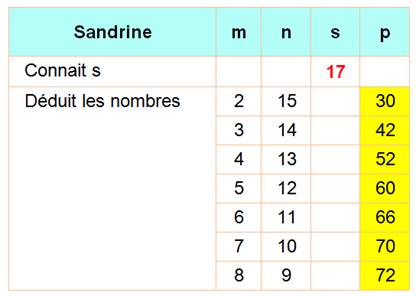
Exemple: Sandrine sait que la somme est 17. Il y a sept partitions à deux termes de 17.
|
|
|
|
Avec le premier produit p = 30, Paul aurait
imaginé les paires (2, 15), (3, 10) et (5, 6) et avec ce choix parmi trois
couples, il aurait effectivement répondu, je ne sais pas conclure facilement. Il faut analyser les sept cas comme P = 30 =
2x15 = 3x 10= 5x6; avec (2, 15) la somme est 17 qui se patronne en (2,15),
(3,14), (4,13), (5,12), (6,11), (7,10), et (8,9). Etc. Suite en Impossible
Puzzle – Wikipedia (anglais) |
|
|
|
|||
|
|
Cette exploration nécessite l'examen de
tous les nombres m et n. |
||
|
Table de Paul
|
Nous consulterons la table des produits ambigus notés mm. Elle
commence par : {12, 18, 20, 24, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52 …}. |
||
|
Sandrine se limite
|
La solution minimale est bien sûr: m = 2 et
n = 3 avec s = 5 Si s s = 53 + (s – 53) et p = 53 x (s – 53) Or
53 est un nombre premier. L'autre facteur, s – 53 qui est positif, est
supérieur à 53. Dans ce cas s est plus grand que 100.
Impossible selon l'hypothèse. p aurait donc une factorisation unique. |
||
|
Sandrine établit sa propre liste déduite de celle
de Paul
|
Exemple Sandrine examine m + n = 17 Parmi les possibilités: m = 2 et n = 15 Le produit est 30 et ce nombre est dans la
liste de Paul. Sommes possibles {11,
17, 23, 27, 29, 35, 37, 41, 47, 53}. |
||
|
Comment arrive-t-on à cette liste réduite?
|
|
||
|
|
||
|
|
S = {11, 17, 23, 27, 29, 35, 37, 41, 47, 53}. |
|
|
Là aussi un bon programme
aide bien! |
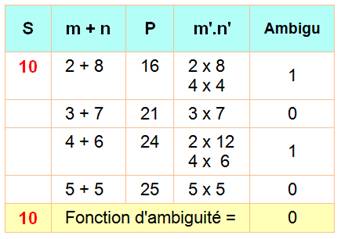
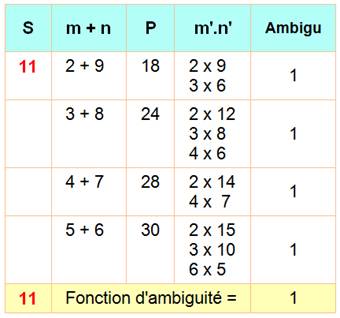
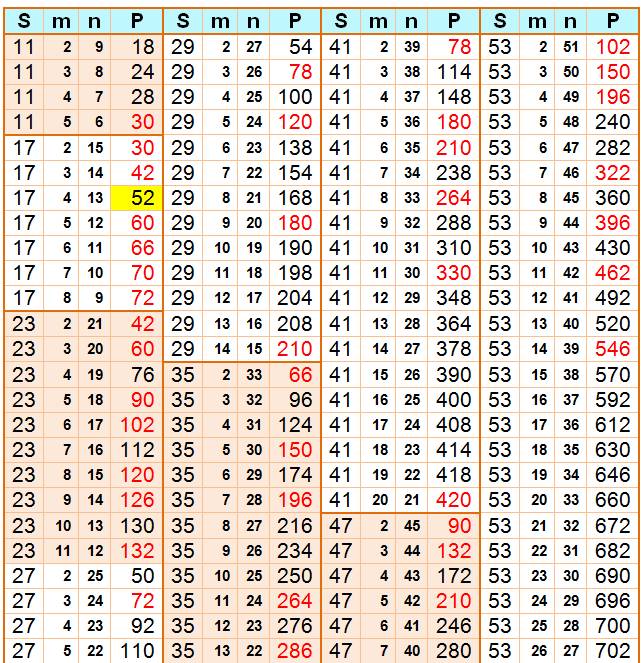
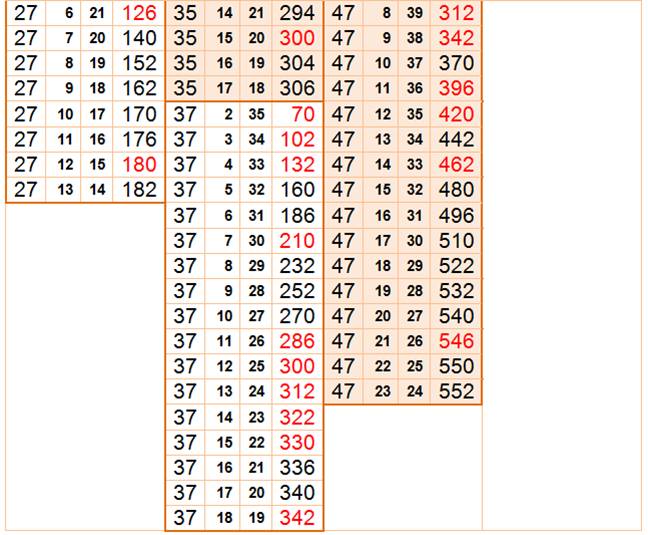
L'ensemble des produit pour S = 11 est
noté: S11 = {18, 24, 28, 30}. Nous remarquons que certains produits se retrouvent
plusieurs fois (en rouge) et seul le produit 52 (jaune) est unique dans
l'ensemble S17. |
|
|
|
||
|
|
Les produits qui apparaissent plusieurs
fois dans la liste sont à éliminer. C'est le cas pour 30, 42, 60, 66 … |
|
|
|
Si le produit appartenait à deux ensembles
Si et Sj, Paul qui connait P et qui sait que S est dans
ce tableau ne pourrait pas savoir quel est le bon nombre. |
|
|
|
p = 52 , m = 4; n = 13 et S = 52. |
|
|
La
limite fixée pour la somme est importante. Elle change la solution! La
même solution est atteinte pour une limite de 65 à 1684. Plus
petite, et le raisonnement n'aboutit pas. La
valeur de 100 est ronde et conduit à un nombre limité de cas à analyser. D'autres considérations sur
la page de JP. Delahaye |
![]()
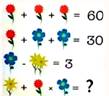
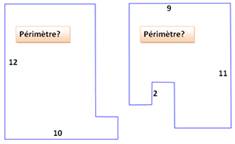
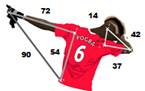
Les problèmes récents présentés par la Presse ou sur Internet
Ces énigmes mathématiques qui rendent fous les internautes; qui affolent
Internet;
qui inondent les réseaux sociaux; les nouveaux casse-têtes des
internautes …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19
descendent et 17 montent, ils sont
63. Combien
avant? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SUITE 2017 et 2018 / 2019
/ Dix chiffres / … |
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
|
|
|
Cette
page |
![]()