|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Problèmes de PESÉES ou des pièces de monnaies Problèmes abordés par
Bachet, Leibniz ou encore Frobenius. On dispose de pièces (ou de poids)
de diverses valeurs. Quelles sont les valeurs qu'il est possibles de
réaliser?
Dans ce dernier cas qu'elle
est la valeur la plus grande non atteignable? Autrement-dit, à partir de
cette valeur toutes les valeurs sont accessibles jusqu'à l'infini? |
Anglais: the coin changing problem
|
|
||
|
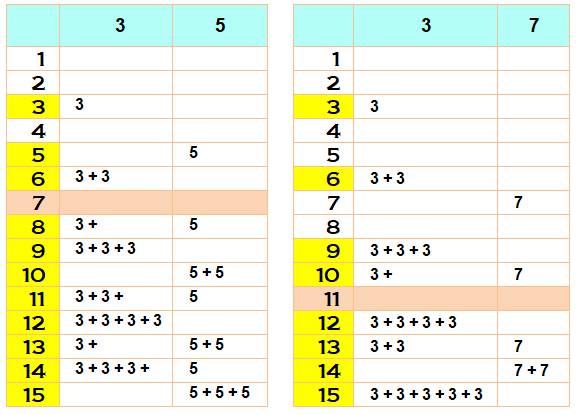
Prenons
deux types de pièces (3 euros et 5
euros) et voyons les sommes possibles avec ces pièces aussi nombreuses que
l'on veut. Évidemment,
impossible de payer des achats à 1 euro ou 2 euros. C'est le cas aussi pour 4
euros. Avec deux pièces de 3 euros, on atteint les 6 euros. Mais, impossible
de combiner les pièces pour former 7 euros. À partir
de 8 euros toutes les valeurs sont faisables. Avec les
pièces de 3 euros et 7 euros, la plus grand somme infaisable est 11 euros.
Notez dès à présent que: 7 =
(3 – 1)(5 – 1)
– 1 11 = (3 –
1)(7 – 1) – 1
|
||
|
Cas simples |
Dés que
l'on dispose d'une pièce de 1 euro, il est possible d'atteindre toutes les
valeurs. Avec les
pièces de 2 et 3 euros |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |