|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère
sans que nous le sachions a priori |
![]()
|
Énigme de la pesée impossible des DOUZE BALLES ou BILLES, BOULES, PIÈCES Méthode classique par dichotomie Fameuse énigme qui semble
impossible à résoudre. La solution est
effectivement difficile à trouver. Pour vous lancer voyez les neuf balles dont une lourde >>> Ou encore, les quatre balles dont une lourde ou légère >>> |
|
|
Ces pages
vous proposent:
La
méthode que je vous propose permet de suivre les pesées successives et,
surtout, les déductions logiques
évidentes à en tirer. |
|
|
|
||
|
Parmi
douze balles de forme identique, une seule est un intrus: une seule n'a pas
le même poids que les autres; elle est plus lourde ou plus légère. En utilisant
une balance à deux plateaux et avec trois pesées seulement, trouvez l'intrus
et sa nature. Aucun
poids n'est admis! |
Anglais: You are given a set of scales and 12 marbles. The 12 marbles appear to
be identical. In fact, 11 of them are identical, and one is of a different weight,
lighter or heavier than the others. Using a pair of scales, determine in three weightings which ball is
the odd one and whether it is lighter or heavier. |
|
|
|
||
|
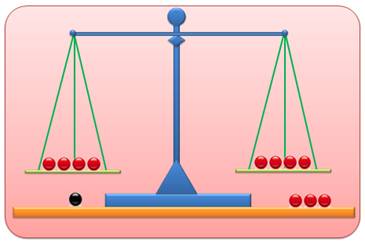
La pesée
sera notée simplement par la symbolisation du fléau. |
|
|
|
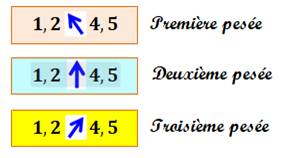
Les trois
pesées sont repérées par une couleur. |
|
|
|
|
||
|
Exposant indiquant l'issue de la
pesée Après une
pesée, chaque balle est qualifiée par un signe plus, égal ou moins selon que
la position des plateaux. |
|
|
|
Intérêt de la notation Deux
conclusions sont possibles à partir de ces deux pesées:
|
|
|
|
|
|
|
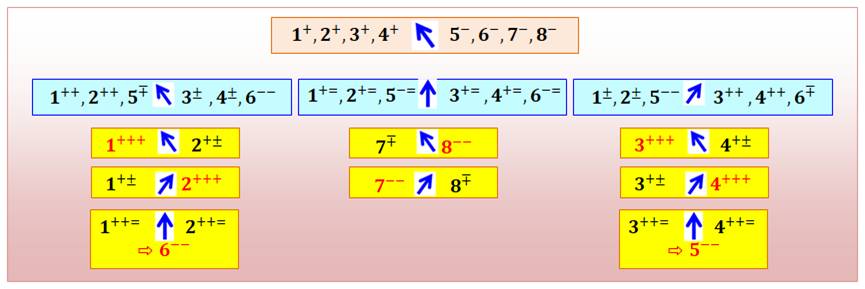
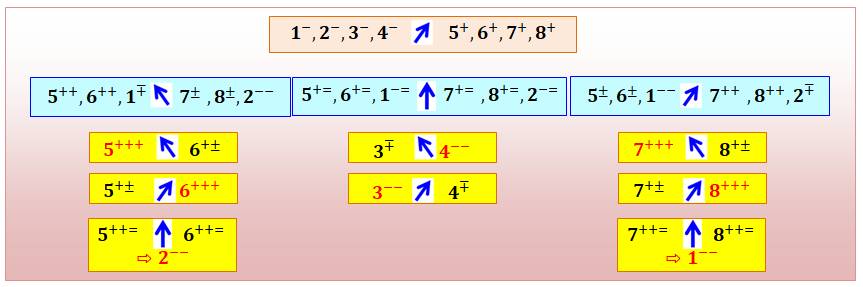
La
première pesée consiste à compare deux lots de quatre balles (disons: 1, 2,
3, 4 et 5, 6, 7, 8) Les trois
possibilités sont examinées dans les trois tableaux suivants: Première pesée avec plateau de gauche
plus lourd
En haut à gauche, la deuxième pesée montre que
seules 1, 2 et 6 sont cohérents. Il s'agit de conclure parmi ces seules trois-là.
Les trois autres (3, 4 et 5) sont normales. En rouge, à l'issue de la troisième pesée, on ne
retient que la balle dont la notation des pesées est cohérente. 1+++ indique
que les trois pesées ont placé cette balle en potentiellement plus lourde à trois
reprises. La balle 1 est l'intrus et elle est plus lourde. Par contre: 2 ++–
indique que la balle pourrait être plus lourde, plus légère ou normale: elle
est donc normale. Au centre, cas d'une pesée en équilibre, on
compare alors les deux boules (7 et 8) qui avaient été laissées de côté. En bas à gauche (comme à droite), la dernière
pesée est en équilibre. C'est que 6– –, la seule balle cohérente lors de la
pesée précédente, est à retenir: la balle 6 est plus légère. |
|
Astuce de la pesée
|
On compare quatre balles normales ou plus lourdes (1, 2) à (3 et 4),
en embarquant également dans la pesée deux balles qui sont potentiellement
plus légères (5 et 6). La troisième pesée en équilibre montre toute la
puissance de cette astuce. Note: cette méthode
utilise des pesées successives par 4 puis par 3 et enfin par 2 billes sur un
plateau, d'où le nom de dichotomie. La méthode par
combinaisons utilise des pesées par 4, 4 et 4. Remarques *Pour être plus précis: dichotomie veut dire couper en
deux. J'utilise le terme pour signifier un concentration progressive même si
la réduction n'est pas de moitié. Deuxième remarque: on
pourrait aussi appliquer le mot de "trichotomie" pour indiquer que
les billes à peser sont réparties en trois groupes. |
|
Tableau des pesées et
conclusions – Suite |
|
|
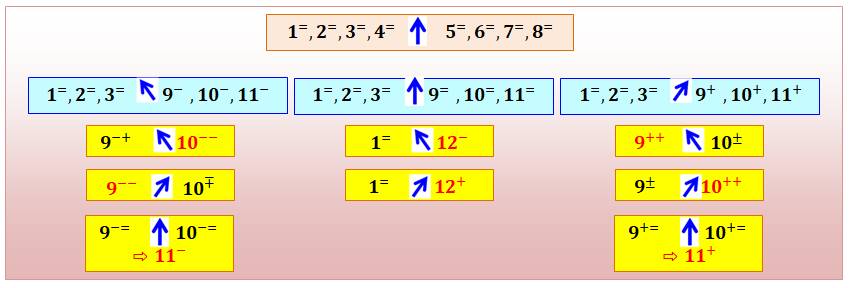
Première pesée avec plateau de
droite plus lourd
Ce tableau est totalement semblable au premier.
Première pesée avec équilibre des
plateaux
Les balles normales (1, 2, 3) sont utilisés comme témoins de
pesée. On pouvait choisir trois balles
parmi les huit connues comme normales. |
|
|
Les trois tableaux montrent les résultats des trois pesées
et couvrent bien les 24 possibilités (1 parmi 12 plus lourde ou 1 parmi 12
plus légère). La répartition des billes lors de la deuxième pesée est
déterminante. Il existe des variantes qui tiennent compte du fait que dès
la première pesée on connait quatre ou huit balles normales qui peuvent
servir en tant que telles dans les pesées. |
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
|
|
|
Sites |
|
|
Cette
page |
![]()