NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/10/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	OUTILS Mathématiques
Débutants Général	Diagonale de CANTOR			Glossaire Général
INDEX Outils Infinis		Aleph0, Aleph 1	Démonstration
		Sommaire de cette page >>> Approche >>> En binaire infini >>> Infini plus un? >>> Rationnels et réels

Diagonale de CANTOR

Comment faire la liste de tous les nombres imaginables, et, cependant, en trouver encore d'autres ? Comment prouver qu'il existe plus d'un seul type d'infinis !

Approche
Choisissez quatre nombres de quatre chiffres et formez un nouveau (5^e) nombre. en faisant plus 1 comme indiqué => Nous venons de créer un nouveau nombre obligatoirement différent des précédents. Pourquoi? Le premier chiffre et différent de celui du premier nombre Le deuxième chiffre est différent de celui du deuxième nombre Etc. Au final, chaque chiffre du nouveau nombre est différent de celui d'un des nombres du tableau de départ.	4 5 6 7 2 3 8 9 9 8 7 6 5 5 5 5 5 4 8 6 Le nombre 5486 est un nouveau nombre, différent de ceux déjà dans le tableau. Cette construction est la base de la démonstration par la diagonale de Cantor.

En binaire … infini
On peut même utiliser les nombres exprimés en binaire Simple commodité! Alors, on prend les chiffres sur la diagonale, en les inversant. Nous n'avons fait aucune restriction sur la quantité de chiffres (colonnes) et de nombres (lignes). Ça marche pour un tableau aussi grand que l'on veut Même … infini! Quelle que soit la quantité de nombres que je pourrai mettre dans le tableau, il en existera toujours un autre différent de tous ceux-ci.	1 1 1 1 1 0 0 1 0 0 0 1 0 1 1 0 0 1 1 1 Aussi grand que l'on veut 1 1 1 1 … 1 0 0 1 … 0 0 0 1 … 0 1 1 0 … … 0 1 1 1 … Même infini!

OUP! Infini + 1 ?
Nous nous trouvons devant une espèce de paradoxe. Nous nous efforçons de mettre tous les nombres possibles et imaginables dans un tableau. Et, pourtant, quoique l'on fasse, il en existera toujours un en plus. Cantor en déduit qu'il existe un infini plus grand, soit, plusieurs sortes d'infinis. De cette découverte, Cantor en fut lui-même étonné, voire effrayé. Tirons en les conséquences pour les nombres réels…

RATIONNELS & RÉELS
Nous allons prendre les nombres décimaux compris entre 0 et 1; ceux qui commencent par 0, … Avec la règle de la diagonale de Cantor, il est toujours possible de former un nouveau nombre, quel que soit l'inventaire que nous puissions produire.
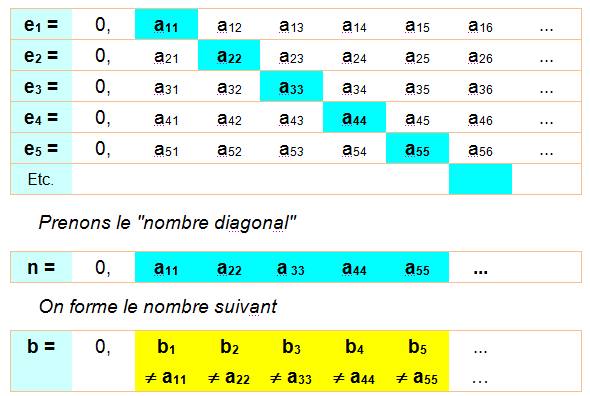
Quelle est la propriété du nouveau nombre créé b? b est bien un réel compris entre 0 et 1 et, par construction, il n'appartient pas au tableau de correspondance. C'est un nombre en plus! Nombres réels L'application de la diagonale de Cantor montre que le tableau ne contiendra jamais tous les nombres réels.	Création de b Pour fixer les idées, on peut prendre bi = 2 si aii = 1 et bi = 1 si aii   1 Comparaison de b à tous les ei Si je compare b à ei, il y aura au moins une ligne de ei, quelque part, dans laquelle une des décimales sera différente. Exemple Pour e3, et par construction, le troisième chiffre de b est différent du troisième chiffre de e3 b3 a33
On montre que: Les réels sont plus nombreux que les rationnels; il y en même beaucoup, beaucoup plus! Voir Diagonale des rationnels Ces deux ensembles ne sont pas équipotents (en bijection). Les réels font partie de l'ensemble c supérieur en cardinalité à Aleph 0. Voir hypothèse du continu Au delà? Oui! Il y a des infinis plus grands que les autres.	Généralisation Ceci est vrai pour tous les chiffres de b B est un nouveau nombre Un nombre en plus. Par exemple L'ensemble des courbes géométriques est plus grand que celui des points géométriques: On atteint un troisième ordre d'infini. >>>

Suite	Aleph 0 et Aleph 1 – Démonstration
Voir	Infini Compter les nombres
Aussi	Inventaire des outils mathématiques Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/aMaths/Outils/DiagCant.htm