|
|||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PREMIERS Recherche sur le tableur Excel La recherche des
nombres premiers sur tableur
peut prendre plusieurs formes:
Je vous propose
d'arriver à établir cette formule pas à pas. Le résultat de
cette page mérite vraiment le détour, même s'il faut s'accrocher un peu pour
aller jusqu'au bout. Cependant si vous voulez ignorer les explications, allez
directement à la formule et mettez la dans votre tableur. Ça marche! |
|
|
||
|
|
Si une seule division donne un reste nul, le nombre est divisible; il
est composé; il n'est pas premier. Autre formulation: Si aucune division ne donne un reste nul, alors, N est un nombre
premier. |
|
|
|
Si N mod (k) pour tous les k = {de 1 à N-1}, alors N est premier. |
|
|
|
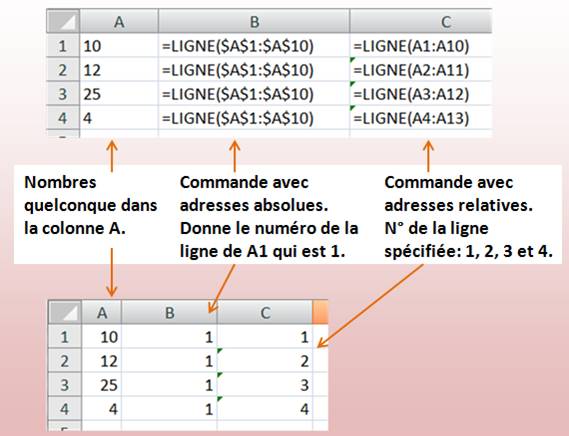
"LIGNES" et "INDIRECT" sont
des commandes Excel qui vont nous permettre d'accéder aux numéros des lignes. |
|
|
|
Le tableur Excel recèle la faculté de travailler
en interne sur des tableaux (matrices) et d'en "sortir" le résultat
dans une seule cellule. |
|
|
|
|
|
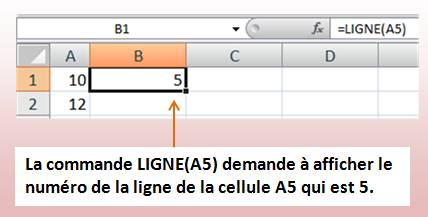
Note: Le contenu de A5 n'a aucune influence.
|
|
|
|
|
|
|
|
|
|
|
|
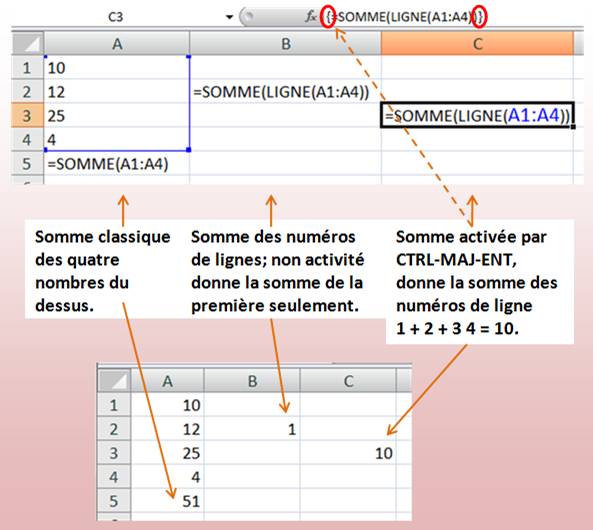
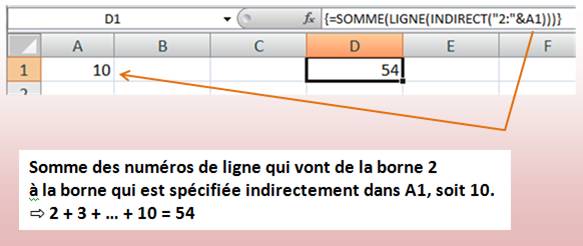
Note: si nous demandons SOMME(2:10), nous aurons le calcul de la somme de tous les
nombres qui se trouve sur les lignes de 2 à 10, quelles que soient les
colonnes, à condition de faire CRTL-MAJ-ENT. |
|
Voir Esperluette
|
|
|
|
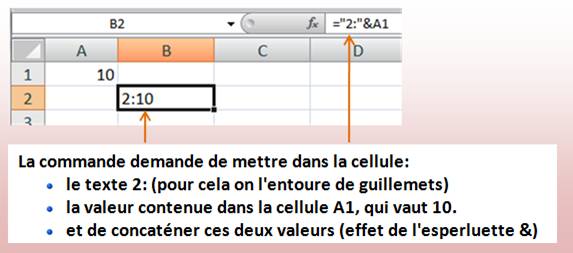
LIGNE(INDIRECT("2:"&A1)) |
|
|
|
|
|
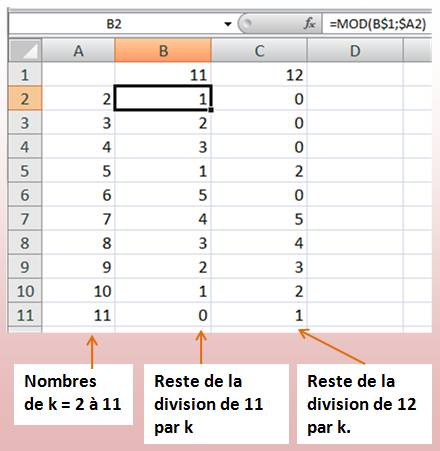
MOD
(nombre, diviseur) MOD
(A1 où se trouve N, les nombres k de 2 à N-1, les uns après les autres) MOD(A1;LIGNE(INDIRECT("2:"&A1-1))) |
|
|
|
|
|
Le
reste 1 et le reste 2 et
… et le reste N-1 sont différents de 0. En langage plus
proche du tableur: ET(reste1; reste2; …
reste N-1) <> 0
Si (
ET ( (reste1; reste2; … reste N-1) <> 0); "premier"; composé" ) Entre guillemets
pour indiquer de mettre ce texte dans la cellule. |
|
|
|
|
|
|
|
|
=SI( |
|
|
; |
"premier";"composé") |
||||||
|
|
ET( |
|
) |
|
|
|||||
|
|
|
(MOD |
|
|
<>0) |
|
|
|
||
|
|
|
|
(A1; |
|
) |
|
|
|
||
|
|
|
|
|
LIGNE( |
|
) |
|
|
|
|
|
|
|
|
|
|
INDIRECT("2:"&A1-1) |
|
|
|
|
|
|
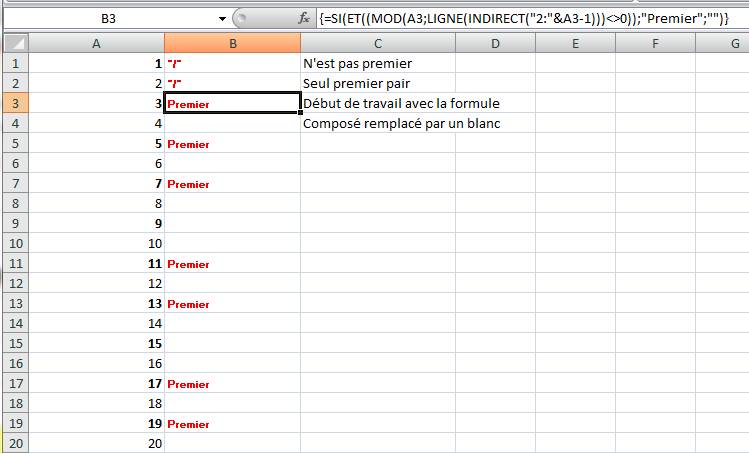
=SI(ET((MOD(A1;LIGNE(INDIRECT("2:"&A1-1)))<>0));"premier";"composé") |
||||||||||
|
Bien indiquer le nom de la cellule où se trouve N.
Ci-dessus en A1; dans l'exemple ci-dessous en
A3. Les cellules B1 et B2 pour N = 1 et N = 2 ne sont pas calculées car
triviales.
|
||||||||||
|
Vous
pouvez copier et coller la formule ci-dessus en B1.
Tapez
un nombre en A1. vous avez la réponse immédiatement. Vous
pouvez tirer les cellules vers le bas obtenir la primalité des nombres
suivants. Vous
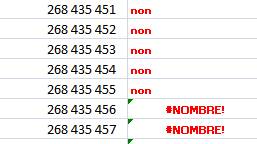
pourrez tester la primalité de N jusqu'à 228 – 1 = 268 435 455. |
Voir Puissances de 2
|
|
|
|
|
|
|
=SI(ET((MOD(A1;LIGNE(INDIRECT("2:"&ARRONDI.SUP(RACINE(A1);0))))<>0));"Premier";"") |
|
ATTENTION!
|
Pour
activer la formule ne pas oublier de
|
![]()
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()