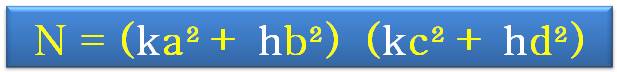|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Identité de BRAHMAGUPTA-FIBONACCI Généralisation
par application linéaire
|
Voir page similaire: Somme de deux carrés et imaginaires
|
|
||
|
La formule originale
est simple; elle peut être généralisée par combinaison linéaire Par exemple en ajoutant
un coefficient devant b et d Notez la place non
symétrique du N dans la somme des carrés |
N
= (a² + Nb²) (c² + Nd²)
= (ac + Nbd)² + N (ad – bc)²
= (ac - Nbd)² + N (ad + bc)² Exemple 369
= 9 x 41
= (1² + 2x2²) (3² + 2x4²)
= (1x3 + 2x2x4)² + 2(1x4 - 2x3)² = (1x3 - 2x2x4)² + 2(1x4 +
2x3)² =
13² + 2 x 10² |
|
|
|
||
|
Idem mais En ajoutant un
coefficient devant a et c |
N
= (Ma² + b²) (Mc² + d²)
= (Mac + bd)² + M (ad – bc)²
= (Mac - bd)² + M (ad + bc)² Exemple 204
= 6 x 34
= (2x1² + 2²) (2x3² + 4²)
= (2x1x3 + 2x4)² + 2(1x4 - 2x3)²
= (2x1x3 - 2x4)² + 2(1x4 +
2x3)²
= 2² + 2 x 10² |
|
|
|
||
|
Combinaison des deux
cas précédents En ajoutant un
coefficient devant a et c et un autre
devant b et d |
N
= (Ma² + Nb²) (Mc² + Nd²)
= (Mac + Nbd)² + MN (ad – bc)²
= (Mac - Nbd)² + MN (ad + bc)² Exemple 500
= 10 x 50
= (2x1² + 2x2²) (2x3² + 2x4²)
= (2x1x3 + 2x2x4)² + 2x2(1x4 - 2x3)²
= (2x1x3 - 2x2x4)² + 2x2(1x4 +
2x3)²
= 10² + 20² |
|
|
|
|
|
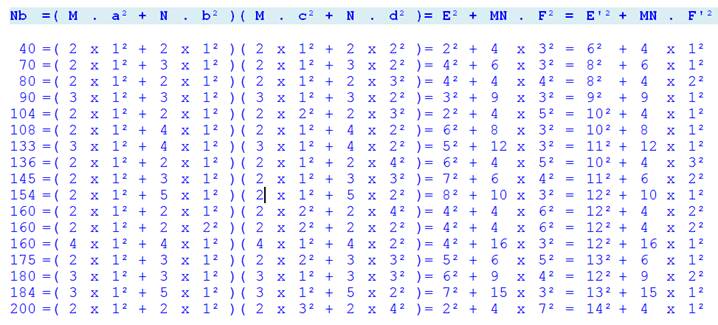
Valeur de N = (Ma² + Nb²) (Mc² + Nd²) =
E² + MnF² = E'² + MNF'² Tous les cas ou E et F
ne sont pas nuls sont listés pour M et N supérieurs
à 1 et pour Nb < 201
|
|
|
|
|
|
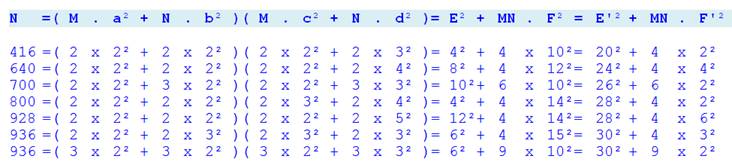
Valeur de N = (Ma² + Nb²) (Mc² + Nd²) =
E² + MnF² = E'² + MNF'² Tous les cas ou E et F supérieurs à 1 sont listés pour M et N supérieurs
à 1 et pour Nb < 201
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Biographies |
|
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Puissanc/Carres/BrahmaGe.htm
|
![]()