|
||||||||||||||||||||||||||||
![]()
|
MULTIPLES & DIVISEURS Chemins eulériens Graphe divisoriel ou chaine de
divisibilité* Vous connaissez le jeu qui consiste à suivre un dessin
sans lever le crayon. Le tracé suit alors un chemin eulérien. L'idée ici consiste à
exécuter un tracé reliant les nombres entiers avec pour règle que le
nombre suivant est un multiple
ou un diviseur
du précédent. Un bon jeu pour enfants et adultes; propice exercices de
programmation; et, un terrain pour les adeptes de la théorie des nombres. Pour ces derniers, les questions qu'ils se posent:
|
* Divisibility chain: chaine de divisibilité.
Au sens strict: un élément de rang n est divisible
par un de rang m si n est divisible par m
|
|
||||||||||||||||||||||||
|
Défi Nombre de
1 à n organisés tels que chacun est le multiple (M) ou le diviseur (D) du
suivant. Sur la première ligne: 3 est un multiple de 1. Le nombre 1 est un diviseur de 2. Sur la dernière ligne (n = 4): 4 est multiple de 2; 2 est un
diviseur de 1; 1 est un
diviseur de 3 Jusqu'à
présent rien de plus simple, voire banal ! |
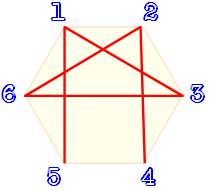
n = 3 – Deux possibilités: 312 et
213
n = 4 – Quatre possibilités
|
|||||||||||||||||||||||
|
Remarque sur les nombres premiers Un nombre
premier ne peut être précédé ou suivi que du 1, et pas les deux à la fois ! Ce qui
impose que le nombre premier (en jaune) est en début ou fin de liste. Sauf,
s'il y a parmi les nombres de 1 à n, un multiple de P. Ce sera le cas pour n
= 6, avec P = 3. |
P est un nombre premier
Il existe un multiple de P
|
|||||||||||||||||||||||
|
Avec le 5, présence de deux nombres
premiers Ces deux
nombres premiers sans multiples sont obligatoirement placés en tête et queue de
liste, laissant l'un d'eux orphelin. |
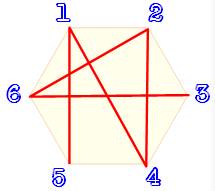
n = 5 – Pas de solution en un seul
chemin
Il existe deux
chemins: 3124 et 5. |
|||||||||||||||||||||||
|
Présence du 6 comme multiple de 3 Les deux
nombres premiers
Nécessairement
le 6 est voisin du 3. Seul 2
divise 6, reste 4, multiple de 2. Finalement,
quatre solutions sont possibles symétriques deux à deux. Défi équivalent: dessiner un chemin
eulérien Comment
relier les nombres par un trait continu (sans lever le crayon) tout en
respectant la règle. |
n = 6 – Quatre chemins symétriques
deux à deux
Les deux chemins eulériens
|
|||||||||||||||||||||||||
|
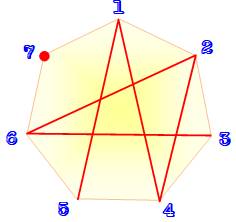
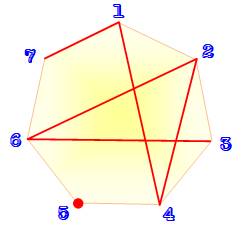
Avec un nombre premier
supplémentaire Impossible
de réaliser le défi. Il se résoudre
à accepter deux suites. En
arrivant à 11, il faut trois suites. Avec 13,
une en plus, etc. |
n = 7 impose deux boucles
|
|||||||||||||||||||||||||
|
|
||||
|
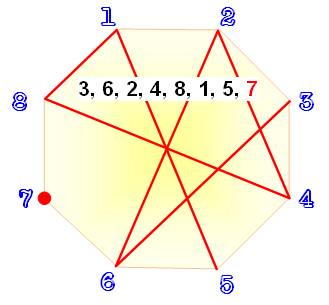
Recherche du chemin le plus long Il est
entendu qu'à partir de 7, il existe plusieurs chemins eulériens (Ch), et
c'est inévitable. Le prochain
défi consiste, malgré tout, à trouver le chemin le plus long parmi les 7! = 5
040 permutations des nombres de 1 à 7. Avec n =
7, il y toujours 2 chemins (Ch = 2). Il y a seize chemins de longueur maximale
(Q = 16), en l'occurrence L = 6, soit, tous les nombres sauf un. |
n = 7, L = 6, Ch = 2 et Q = 16 3, 6, 2, 4, 1, 5, 7 3, 6,
2, 4, 1, 7, 5 4, 2,
6, 3, 1, 5, 7 4, 2,
6, 3, 1, 7, 5 5, 1,
3, 6, 2, 4, 7 5, 1,
4, 2, 6, 3, 7 5, 3, 6, 2, 4, 1,
7 5, 4, 2, 6, 3, 1, 7 5, 7,
1, 3, 6, 2, 4 5, 7, 1, 4, 2, 6, 3 7, 1,
3, 6, 2, 4, 5 7, 1,
4, 2, 6, 3, 5 7, 3, 6, 2, 4, 1, 5 7, 4, 2, 6, 3, 1, 5 7, 5, 1, 3, 6, 2, 4 7, 5, 1, 4, 2, 6, 3 Exemples en jaune => |
|
||
|
n = 8, L = 7, Ch = 2 et Q = 32 Un des exemples
=> n = 9, L = 8, Ch = 2 et Q = 32 Comme: 4, 8, 2, 6, 3, 9,
1, 5, 7 n = 10, L = 9, Ch = 2 et Q = 80 Comme: 4, 8, 1, 5, 10, 2,
6, 3, 9, 7 N = 11 à 13 Ch = 3 Éric
Saias, enseignant-chercheur à Sorbonne Université, a montré que le nombre minimal
de chemins pour couvrir les entiers de 1 à n était supérieur à n/6 pour tout entier n. |
|
|||
|
Jusqu'à
n = 10, il existe 3 628 800 (= 10!) permutations
des 10 nombres. Une
recherche "force brute" des permutations qui satisfont la règle de
construction des suites de nombres est assez facile à implémenter. Au-delà,
pour éviter la saturation de la mémoire et limiter le temps de calcul,
d'autres pistes doivent être mise en œuvre. Un
algorithme s'appuyant sur une table des diviseurs permet de limiter les
chemins d'exploration et de calculer nombres après nombres. Il faut alors
maitriser la gymnastique du cheminement dans les arbres (retour vers la
bifurcation précédente, par exemple). Programmation avancée ! |
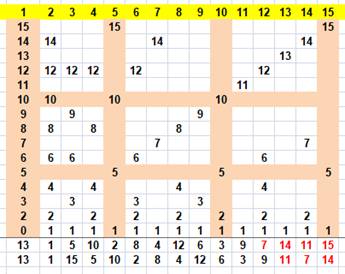
Exemple de disposition pour aide avec tableur
|
Création
des colonnes des diviseurs de 1 à 15 par exemple. Deux
exemples d'essais sur les deux lignes en bas. En
commençant par 13, suivi du 1, on a choisit 15 pour suivre, amenant le 5,
puis le 10, … La
dernière ligne est représentée sur le graphe qui suit.. |
|
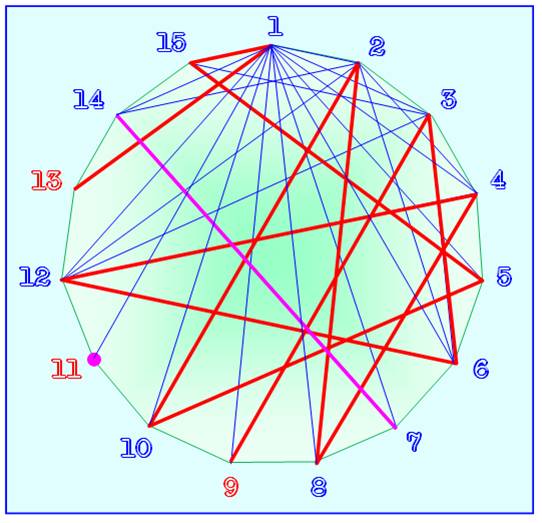
Exemple de trois chemins avec n = 15
En bleu, toutes les
possibilités de routes
|
|
||
|
Défi n°2 Trouver
une suite de nombres telle qu'elle contienne tous les nombres de 1 à N, une seule fois, quelle que soit les nombres
utilisés. Les
nombres utilisés peuvent, bien entendu, dépasser N. L'algorithme
de construction semble simple. Mais les nombres intermédiaires croissent
rapidement. Est-il
possible de trouver d'autres solutions avec des nombres moins grands ? Les mathématiciens Éric Saias et Pierre Mazet ont
montré qu'il est possible de construire une chaîne de divisibilité en
s'assurant que le énième terme demeure toujours plus petit que:
Note: cette suite de nombres est répertoriée en OEIS- A064736. |
Exemple 1, 2, pour obtenir le 3, on passe par le 6 = 2 x
3. 1, 2, 6, 3, pour le 4, on fait 3x4 = 12 1, 2, 6, 3, 12, 4, 20, 5 le 6 est déjà présent,
passons au 7: 5 x 7 = 35 …5, 35, 7, 56, 8, 72, 9, 90, 10, etc. Jusqu'à 100 1, 2, 6, 3, 12, 4, 20, 5, 35, 7, 56, 8, 72, 9,
90, 10, 110, 11, 143, 13, 182, 14, 210, 15, 240, 16, 272, 17, 306, 18, 342,
19, 399, 21, 462, 22, 506, 23, 552, 24, 600, 25, 650, 26, 702, 27, 756, 28,
812, 29, 870, 30, 930, 31, 992, 32, 1056, 33, 1122, 34, 1224, 36, 1332, 37,
1406, 38, 1482, 39, 1560, 40, 1640, 41, 1722, 42, 1806, 43, 1892, 44, 1980,
45, 2070, 46, 2162, 47, 2256, 48, 2352, 49, 2450, 50, 2550, 51, 2652, 52,
2756, 53, 2862, 54, 2970, 55, 3135, 57, 3306, 58, 3422, 59, 3540, 60, 3660,
61, 3782, 62, 3906, 63, 4032, 64, 4160, 65, 4290, 66, 4422, 67, 4556, 68,
4692, 69, 4830, 70, 4970, 71, 5183, 73, 5402, 74, 5550, 75, 5700, 76, 5852,
77, 6006, 78, 6162, 79, 6320, 80, 6480, 81, 6642, 82, 6806, 83, 6972, 84,
7140, 85, 7310, 86, 7482, 87, 7656, 88, 7832, 89, 8099, 91, 8372, 92, 8556,
93, 8742, 94, 8930, 95, 9120, 96, 9312, 97, 9506, 98, 9702, 99, 9900, 100 Plus loin … 495, 245520, 496, 246512,
497, 247506, 498, 248502, 499, 249500, 500 … …4995, 24955020, 4996,
24965012, 4997, 24975006, 4998, 24985002, 4999, 24995000, 5000 … |
|
|
|
Programme Maple Excellent petit exercice de programmation. On déclare une liste R avec 1 et 2
pré-positionnés. La boucle de calcul commence à 3 jusqu'au nombre
N désiré (Ici N = 20). Si le nombre n n'est pas déjà dans la liste R (has), on calcule le produit du dernier nombre de
r par n. R[nops(R)] veut dire que dans R
on veut l'élément de rang nops(R) avec nops donnant la quantité d'éléments dans R. La liste R est complétée des deux nouveaux, m (le
multiple) et n (le nombre suivant. En bleu, le résultat du calcul. Notez que le
nombre 20 demandé n'apparait pas en fin de liste. Il est apparu en septième
position. |
|
|
[1, 2, 6, 3,
12, 4, 20, 5, 35, 7, 56, 8, 72, 9, 90, 10] |
Programme Python Définition d'une fonction multiples-diviseurs. Exactement mêmes instructions qu'en Maple. À noter: boucle jusqu'à
n + 1 pour avoir un résultat jusqu'à n inclus. La non-appartenance s'exprime simplement par not in (pas dedans). Accès au dernier élément de la liste (comme
possible aussi avec Maple) par l'indice -1. Ajouter un élément se fait aves append
(apposer), mais un seul élément à la fois. |
|
Voir Programmation – Index / Python
– Index
|
Le
jeu consiste à réaliser une suite de nombres tels que le suivant Une
grille des nombres de 1 à 100 sert de support au jeu (illustration). Le premier joueur fait un choix, le second
enchaine. Les nombres choisis sont barrés au fur et à mesure. On
montre que le second joueur peut toujours gagner la partie. Un exercice de
programmation consiste à faire jouer l'ordinateur en second et l'amener à
gagner à tout coup. Exemple
de partie: 14, 2, 62, 31, 93, 3, 57, 19, 95, 5,
55, 11, 77, 7, 91, 13, 65. Voir le lien pour son implémentation
Scratch Allez dans le projet (voir à
l'intérieur) pour rendre visible la liste des nombres joués. |
Page imaginée d'après
l'article de Roger Mansuy
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/MulDiv.htm |
|
![]()