NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/12/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TOPOLOGIE
Débutants Géométrie	QUATRE COULEURS OUTILS				Glossaire Géométrie
INDEX Quatre couleurs	Graphes	Relation d'Euler	Nombre chromatique	Chaine de Kempe
		Sommaire de cette page >>> Approche >>> Détermination du nombre chromatique >>> Algorithme glouton >>> Anglais

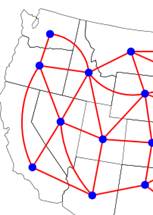
Théorèmes des quatre couleurs

Utilisation des graphes

Une carte colorée est équivalente (duale) à un graphe dont les sommets sont colorés.

Colorer un graphe c'est attribuer une couleur à chacun des sommets, chaque paire de sommets reliée par une arête étant de couleurs différentes.

La quantité minimale de couleur pour colorer le graphe est appelée nombre chromatique du graphe.

Approche
Prenez la carte des pays et donnez une capitale à chaque pays. Pays et capitales sont de même couleur. Si deux pays possèdent une frontière commune reliez les deux capitales. Alors le réseau des liens entre capitales, le graphe, avec ses sommets colorés est équivalent à la carte initiale en termes de coloration.
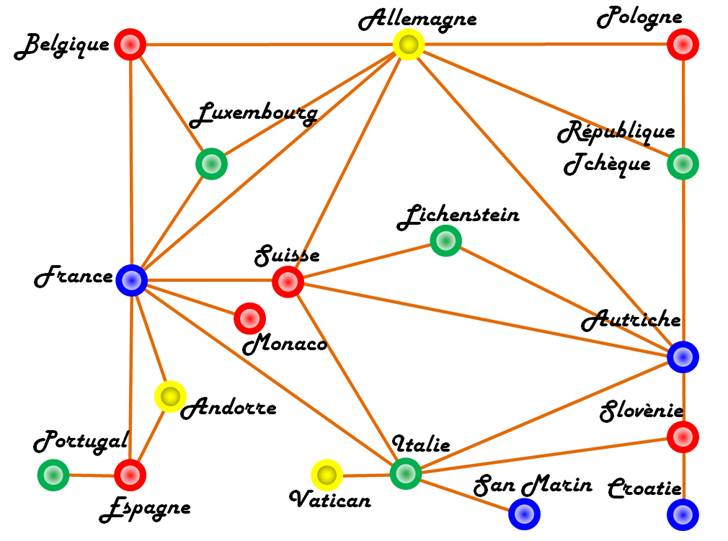
Exemple avec le graphe coloré pour l'Europe occidentale
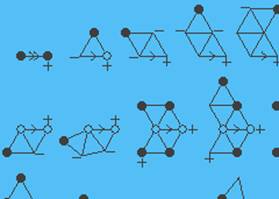
Exemple de graphes analysés par Neil Roberston et al. en 1995. Cet exemple montre la richesse du problème des quatre couleurs et, par là même, la complexité de la résolution.

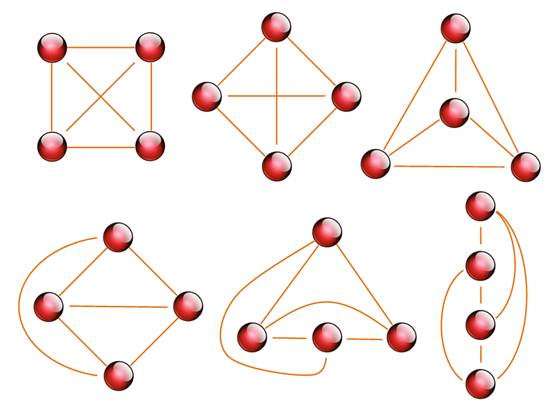
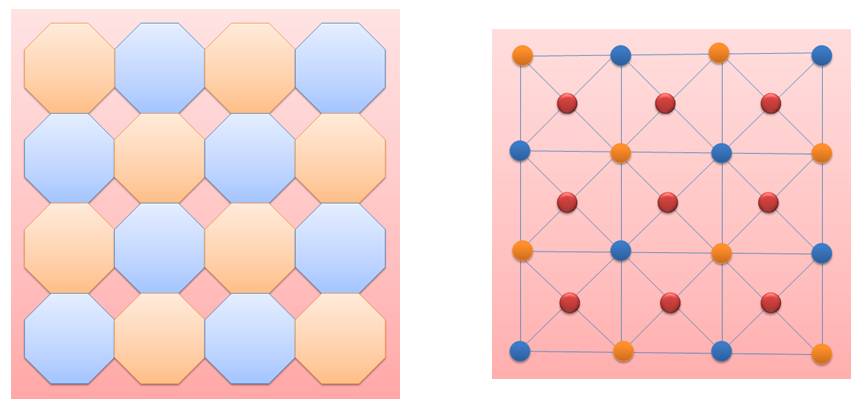
Tous ces graphes sont équivalents

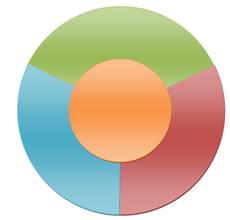
La représentation sous forme de régions de ce graphe. Forme duale du graphe en tétraèdre (en haut à droite). Quatre couleurs sont nécessaires.

Représentations duales

Colorer un graphe et détermination de K
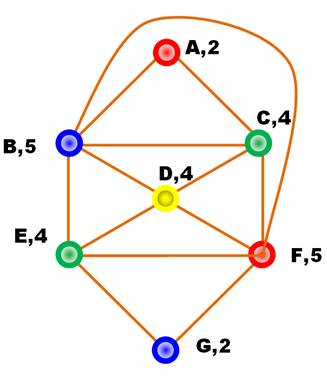
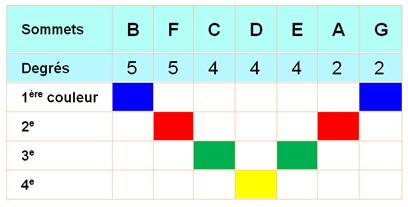
Comment procéder méthodiquement à la coloration de ce graphe et ainsi déterminer son nombre chromatique? Algorithme de Welsh-Powell Dans un premier temps, nous calculons le degré des sommets (quantité d'arêtes). Nous ordonnons les sommets par ordre décroissant (tableau). Ordre quelconque pour les égaux. La première couleur (bleue) est appliquée au premier sommet (B). Elle convient également à tout sommet non connexe à B et non connexes entre eux. Soit G. La deuxième couleur (rouge) est appliquée au sommet suivant (F) et ses compatibles, ici A. Etc. Le nombre chromatique de ce graphe est égal à 4.

Voir Algorithme

Algorithme glouton (vulgairement: "bestial")

Colorer un sommet. Pour le sommet s suivant non colorié, prendre la première couleur dans la palette qui n'a pas été utilisée pour des sommets adjacents au sommet s. Si les couleurs de la palette sont épuisées, c'est qu'il faut y ajouter une couleur.

Cet algorithme ne produit pas la solution optimale. Mais …

Si le degré maximal d'un des sommets est d_max, le maximum de couleurs nécessaires est d+1 ou moins. Ce qui donne une borne supérieure au nombre chromatique.

Anglais: greedy algorithm for coloring vertices

Voir Algorithme glouton de recherche de chemin optimum

English corner

The four-color problem (américain), the four-colour problem (anglais), the 4CT, or the Gunthrie's problem: Does every planar graph have chromatic number 4 or less? The chromatic number is the minimum number of colors needed for a proper coloring. A proper coloring of a graph is an assignment of colors to the vertices of the graph such that every two vertices connected by an edge must receive different colors. Source: The Notorious Four-Color Problem by Jeremy L. Martin (Kansas)

Retour Suite	Quatre couleurs – Introduction Coloration des graphes et relation d'Euler Quatre couleurs – Index
Voir	Cinq pays Couleurs Démonstration Énigme des carrés mitoyens Graphe à 2 couleurs Graphe de Delaunay Indicateur d'Euler-Poincaré Introduction à la topologie Quadrichromie Topologie – Glossaire Topologie – Index
DicoNombre	Nombre 4
Sites	Voir références
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/TopoQGra.htm