|
|||||||||||||||||||||||||||||||||||
![]()
|
À
SIX (et +) autour d'une TABLE RONDE Plusieurs énigmes avec six
ou sept personnes autour d'une table. |
Anglais: The Dinner
Table Problem
En résumé
|
Quantité
de dispositions avec k convives (k personnes):
|
|
|
||
|
Général Nous
avons six personnes à déjeuner autour
d'une table ronde. Il y a 5! = 120 possibilités de le
disposer. (Pas 6! car la table est ronde et les cas supplémentaires
correspondraient simplement à faire tourner la table 6 fois d'un cran de
30°). Notez: Les mots colorés sont très importants! |
Notre défi! Faire en
sorte qu'une personne A n'ait jamais la même paire
de voisins B et C. Le
convive A peut avoir eu plusieurs fois le même voisin B ou C, mais jamais le
même couple (B et C). Chaque personne du couple (B ou C) peut avoir été
voisine de A plusieurs fois. Le défi
est de savoir combien de déjeuners successifs
il est possible d'organiser. |
|
|
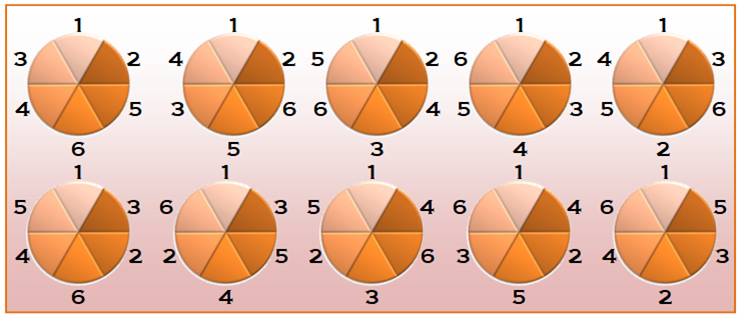
Solution Avec six personnes, il est possible d'organiser
dix déjeuners successifs sans qu'un convive ne voie le même couple de
voisins. Cette
quantité correspond au maximum aux possibilités de choix de 2
voisins parmi 5 = (5x4) / (2x1) = 10.
Le convive 1 ne voie le couple (2, 6) qu'une
seule fois, même s'il reverra séparément le 2 et le 6. Le convive 2 ne voie le couple (1, 3) qu'une
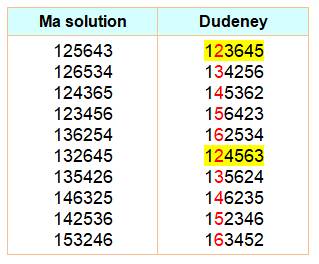
seule fois. Etc. Note Comparaison entre la solution proposée ci-dessus
(vérifiée par programmation) et celle de Dudeney.
Simple effet des choix de départ. Par contre, celle de Dudeney présente une
structure par permutation
circulaire sur les colonnes (hors la première) dans chaque bloc de cinq
lignes avec en jaune la tête de file.
|
||
Anglais: n people
sitting on a circular table without repeating neighbor-sets / an attendee needs
BOTH his neighbors to be new faces,
|
|
||
|
Situation Autour de
la table ronde:
En
parfaits maîtres de maison les époux sont les plus éloignés possibles. Le but
est de retrouver le nom du mari d'Hélène. |
Données 1)
Vincent est assis à la gauche de la femme qui s'est assise à la gauche de
l'homme qui s'est assis à la gauche d'Anne. 2) Jérôme
est assis à la gauche de la femme qui s'est assise à la gauche de Roger. 3) Émilie
est assise à la gauche de l'homme qui s'est assis à la gauche de la femme qui
s'est assise à la gauche de l'homme qui s'est assis à la gauche de la femme
qui s'est assise à la gauche de l'époux d'Hélène. |
|
|
|
|||
|
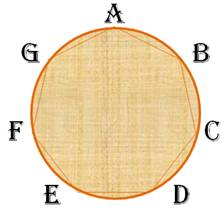
Situation Sept
personnes autour de la table ronde. Ils décident que les prochaines fois
aucun d'entre eux ne se retrouvera à côté de la même personne. Combien
de tels repas peuvent-ils faire? Trois méthodes de résolution. |
Illustration
|
||
|
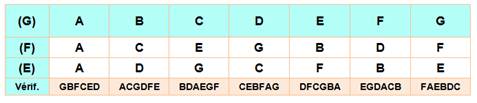
Recherche avec tableau On
développe la table linéairement, La colonne de gauche rappelle le nom du
voisin de droite de A. Pour A
qui a voisiné avec G et B, on essaie les voisins un cran plus loin: F et
C. Puis E et D. Et c'est fini! A est bien passé à côté de
chacun des six autres. |
On constate vite qu'il n'y a que trois
possibilités. En cherchant logiquement les voisins, on trouve la table
indiquée. La dernière ligne vérifie que chacun à bien voisiné l'un des
autres. |
||
|
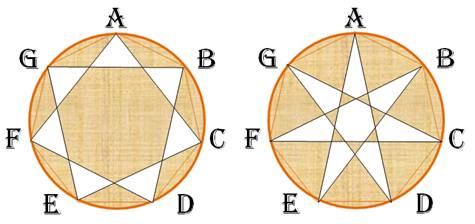
Réponse graphique Seulement
deux autres possibilités. Elles
correspondent aux deux heptagones étoilés. |
Cette représentation graphique montre bien, et commodément, les deux
configurations complémentaires. |
||
|
Dénombrement Quantité
de possibilités avec 6 personnes: |
6! |
||
|
Élimination
des permutations à deux (AB et identique à BA). |
6!
/ 2 |
||
|
Il se
trouve que A est proche de B: |
5
! fois |
||
|
Quantité
de possibilités |
½
6! / 5! = ½ 6 = 3 |
||
Voir Heptagone / Dénombrement / Graphe
|
|
|
|
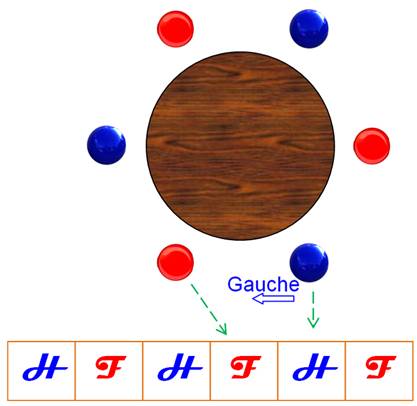
Illustration de la situation Disposition
des six convives autour de la table, en faisant l'hypothèse que les couples
sont alternés, ce qui sera vérifié en étudiant la proposition 3).
On
représente la disposition en un tableau, en notant bien que, par exemple
(flèches vertes), la femme est assise à la gauche du monsieur. |
|
|
Proposition 3) Émilie1 est assise à la
gauche de l'homme2 qui s'est assis à la
gauche de la femme3 qui s'est
assise à la
gauche de l'homme4 qui s'est assis à la
gauche de la femme5 qui s'est
assise à la
gauche de l'époux d'Hélène6. Les
numéros indiquent la quantité de personnes impliquées.
|
|
|
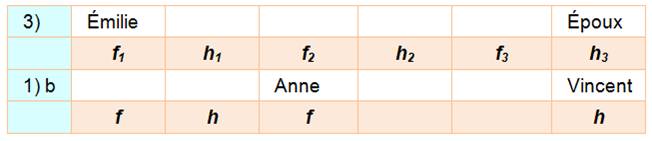
Proposition 1) Vincent1
est assis à la
gauche de la femme2 qui s'est
assise à la
gauche de l'homme3 qui s'est assis à la
gauche d'Anne4. Vincent
peut prendre les positions h1 ou h3. La position h2
n'est pas possible car Anne prendrait la position occupée par Émilie. Option a)
Option b)
|
|
|
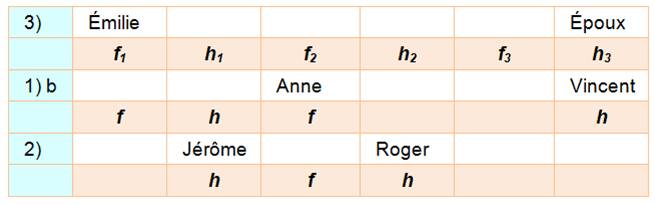
OPTION a) et proposition 2) Jérôme1 est assis à la
gauche de la femme2 qui s'est
assise à la
gauche de Roger3. Jérôme
est installé en h2. En h3 Roger se retrouverait avec
Vincent.
Alors,
Roger en h3 est l'époux d'Hélène en f2. Ils sont
éloignés; en fait, en face l'un de l'autre. Cette solution marche. |
|
|
OPTION b) et proposition 2) Jérôme ne
peut être qu'en h1.
Alors,
Vincent en h3 est l'époux d'Hélène en f3. Ils sont
voisins. Cette
solution ne convient pas. |
|
|
Solution
|
|
![]()
|
Retour |
|
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()