Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 22/01/2021 M'écrire Brèves de Maths

INDEX Polygones Graphe Topologie Logique Jeux	Topologie – Graphes
	Eulérien		Planaire	Multiple et diviseurs		Nœuds
	Lexique		Coloration	Graphe de Delaunay		Fourmis
	Structures rigides	Rigide de longueur constante			Meccano

Graphes ou Polygones Rigides à longueur constante (style allumettes) Le défi consiste à rigidifier le carré (illustration) et autres polygones réguliers en n'utilisant que des barres de la même longueur que les côtés du carré. De nombreux passionnés cherchent les solutions comportant le minimum de barres.
	Sommaire de cette page >>> Rigidité >>> Le carré rigide (braced square) >>> Le carré rigide avec croisements >>> Le pentagone rigide	Débutants Géométrie Glossaire Topologie

Anglais: Braced polygons; a hinged square composed of four equal rods; matchstick solutions for the pentagon

(Polygones rigides; un carré articulé composé de quatre barres égales; solution allumettes pour le pentagone)

Rigidité		haut
Rigide ou déformable Nous nous intéressons aux polygones réalisés avec des barres articulées de même longueur. Montées sur charnière ou même bien vissée, sous la pression, le carré peut se déformer en losange, alors que triangle équilatéral gardera sa forme.	Le triangle est rigide: le carré est déformable.
Polygones réguliers Tous les polygones réguliers sont déformables sauf le triangle.
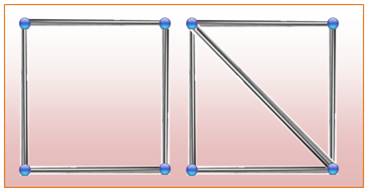
Consolidation Rendre le carré indéformable consiste à créer des triangles dans la structure. La solution la plus simple consiste à ajouter une barre en diagonale. Une seconde diagonale est superflue. Notons que la tige en diagonale est plus longue (racine de 2 fois le côté). Une tige de même longueur en transversal n'est pas autorisée. Alors comment rigidifier le carré avec des barres ayant toutes la même longueur ? Il en faut 23 !	Un carré est rigidifié en ajoutant une diagonale. Una barre supplémentaire est inutile. Une barre transversale de même longueur que les quatre autres n'est pas autorisée.

Le carré rigide (braced square)		haut
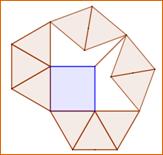
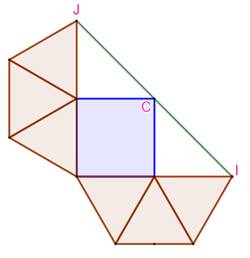
But Constituer un réseau de barres identiques sans croisement, comportant un carré et les éléments nécessaires pour le rigidifier. Solution La solution minimale consiste à composer cette figure comportant 4 + 23 = 27 barres Publiée par Martin Gardner (1964)
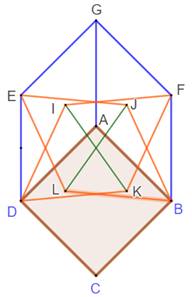
Composition La figure comporte deux parties rigides. Les six triangles équilatéraux qui entourent deux côtés du carré et qui alignent les points ICJ, si le carré n'est pas déformé. La seconde partie (graphe de Moser) forme un triangle (IKJ, vert) maintenu rigide par sa hauteur CK (laquelle remplace la barre habituelle IJ). Les deux parties réunies maintiennent le segment IJ à sa longueur et rigidifie le carré.
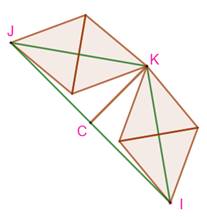
Le triangle vert Si le côté du carré vaut 1, sa diagonale vaut: AC = CJ = On trace CK = 1 dans l'alignement de AC. Alors, CK est perpendiculaire à IJ Dans le triangle rectangle CKJ (théorème de Pythagore): JK² = JC² + CK² = 1 + 2 = 3 JK = Or JK = 2 fois la hauteur du triangle équilatéral soit : Preuve qu'il est possible de loger ces quatre triangles équilatéraux sur les côtés du triangle vert. Pour information l'angle IJK = 35,26…°

Voir Brève de maths n° 581

Le carré rigide avec croisements				haut
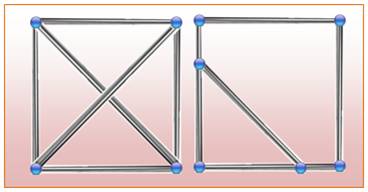
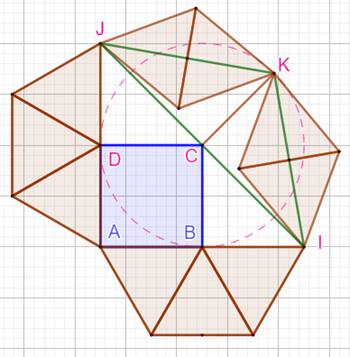
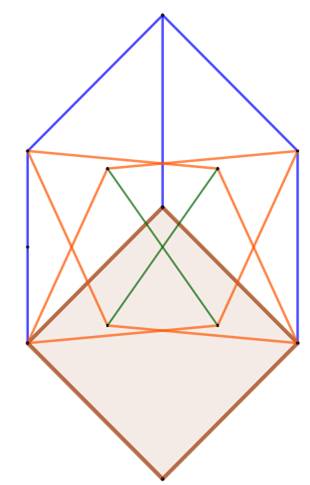
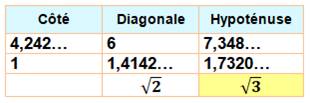
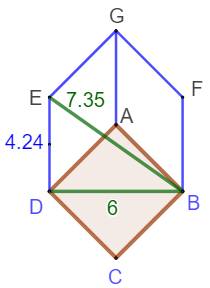
But Constituer un réseau de barres identiques comportant un carré et les éléments nécessaires pour le rigidifier. Les croisements sont permis. Solution La solution minimale consiste à composer cette figure comportant 4 + 15 = 19 barres Justification Sur la figure du bas, on a repéré la diagonale du carré DB en vert et l'hypoténuse du triangle rectangle DBE également en vert. Le dessin a été réalisé avec une diagonale DB du carré qui mesure 6 unités. Le logiciel de dessin indique les valeurs mentionnées sur la figure. En revenant à un carré unité, on constate que la diagonale vaut racine de 2, ce qui est naturel. L'hypoténuse mesure racine de 3, qui est la valeur permettant de loger les losanges orange (DIFK et BLEJ sur la figure en bas à droite). Construction en trois étapes
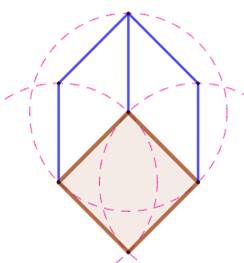
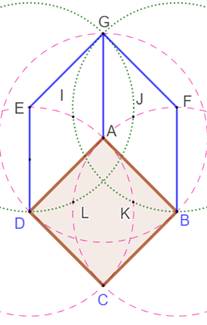
Construction du "cube" Carré ocre de côté unité. Diagonale verticale prolongée. Parallèles à celle-ci passant par les deux autres sommets. Cercles pointillés rose de rayon unité. Segments bleus.	Construction des quatre points centraux Cercles verts de rayon unité. Intersections I, J, K et L avec les cercles rose.		Finalisation Losanges DIFK et BLEJ. Croisillon formé par IK et JL.

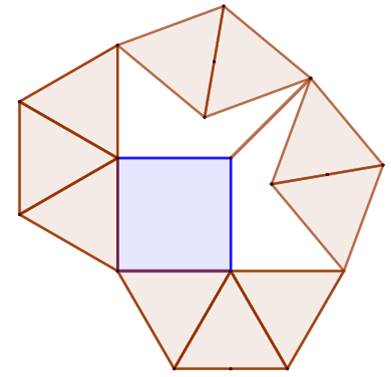
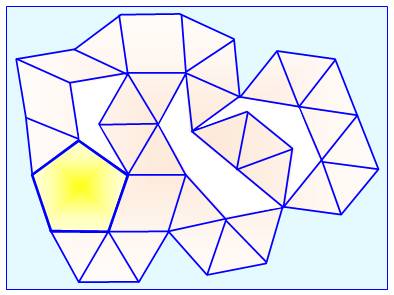
Le pentagone rigide avec 69 barres de même longueur (O'Beirne – 1963)

Haut de page

Retour	Polygones rigides rationnels façon Meccano Polygones rigides en général Carré rigide et autres jeux
Suite	Forces Poutres Géométrie avec des allumettes Graphes – Index
Voir	Allumettes et géométrie
Sites	Discrete geometry – Wikipedia Exploring structural engineering fundamentals – Diaporama – Les bases Rigid Graph – Wolfram MathWorld Braced polygon – Wolfram MathWorld Fundamentals of Structural Engineering – Jerome J. Connor et Susan Faraji – Springer – 2012 – pdf 1159 pages
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/RigideC.htm