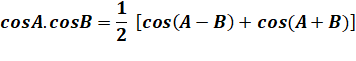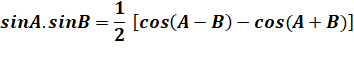|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CALCULS
EN TRIGONOMÉTRIE Méthode
de calcul d'un produit Multiplications et divisions par la trigonométrie Méthode prosthaphaeresis
(grec pour addition et soustraction). Elle consiste à effectuer une multiplication
ou une division
en convertissant les nombres
en angles.
Intérêt historique. Cette méthode de calcul à été éclipsée avec l'avènement
des logarithmes.
Plus pratique, même s'il fallait toujours recourir à une table de
valeurs. Les identités trigonométriques utilisées
remontent à 1510, mentionnée dans un écrit de Johannes Werner. La méthode de
multiplication remonte au moins à Tycho
Brahé en 1580. Elle figure sur un manuel de trigonométrie écrit par son
assistant Paul Wittich. |
|
|
||
|
Relations trigonométriques utilisées: |
|
|
|
Exemple de calcul Aujourd'hui avec calculette;
à l'époque avec des tables trigonométriques ou, plus récemment, la règle
à calcul. |
cosA = 0,123456 => A = 1,447024549 cosB = 0,234567 => B = 1,334023210 |
|
|
Somme et
différence: |
A + B = 2,781047759 => cos = –0,9357047324 A – B = 0,113001339 => cos =
0,9936221398 |
|
|
Moyenne
de ces deux cosinus: |
P = –0,0289587037 |
|
|
À comparer à la valeur donnée par la calculette: |
P = 0,123456 x 0,234567 = 0,028958703552 |
|
Voir Démonstration de ces identités
trigonométriques
|
Programme Maple
|
Notez la
formulation complète du produit P en termes de cosinus et arc cosinus. L'arc
cosinus donne l'angle connaissant la valeur du cosinus. |
Pour mémoire: la multiplication posée
En
bas, la somme en distinguant les unités et les dizaines (retenues)
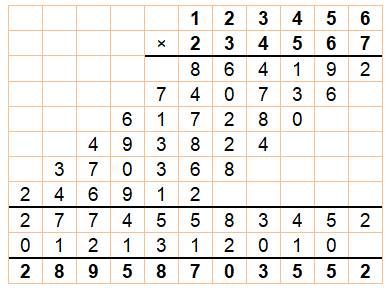
Voir Multiplication
posée
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
![]()