NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres figurés
Débutants Nombres figurés	NOMBRES CARRÉS			Glossaire Nombres carrés
INDEX Carrés Nombres figurés Feuille de route	Introduction	Caractérisation	Carrément carré	Doublement carré
		CatCar	Carré-carré	Doublement cube
		Sommaire de cette page >>> Caractéristiques >>> Liste >>> Carrés avec somme des chiffres en cube

Caractéristiques
Famille	Nombre / Figuré / Carré
Définitions	NOMBRE doublement CARRÉ Nombre carré La somme des chiffres est également un carré Voir Nombres doublement cube
Formule	avec
Exemple	81 = 9² 8 + 1 = 9 = 3²
Propriétés	Certains nomment nombre carrément carré ou doublement carré, les nombres carrés tels que la somme de leur chiffre est également un carré. Il y en a une infinité. Si on considère la racine (n), on peut établir deux classes de nombres: ceux qui possèdent cette propriété {1, 2, 3, 6, 9 …}; ils sont 253 jusqu'à n = 1000 et les autres {4, 5, 7, 8, 16 …}; ils sont 847 jusqu'à n = 1000.

Liste des nombres doublement carré
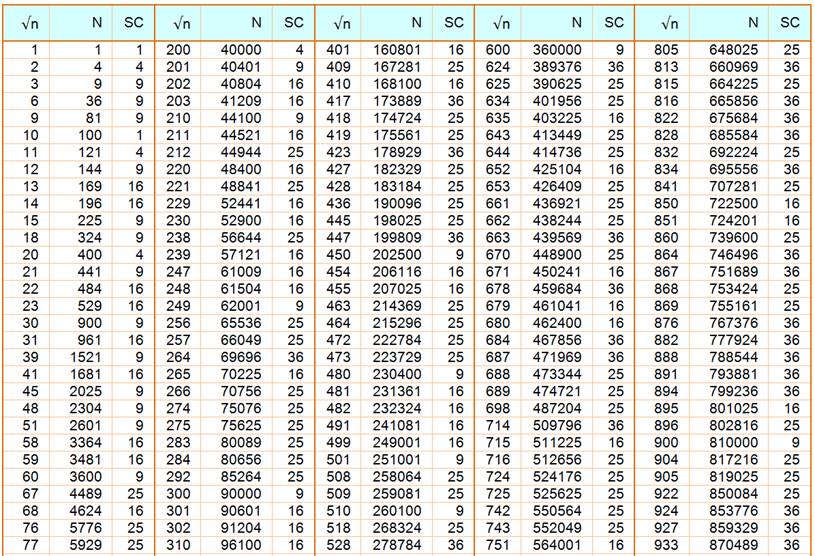
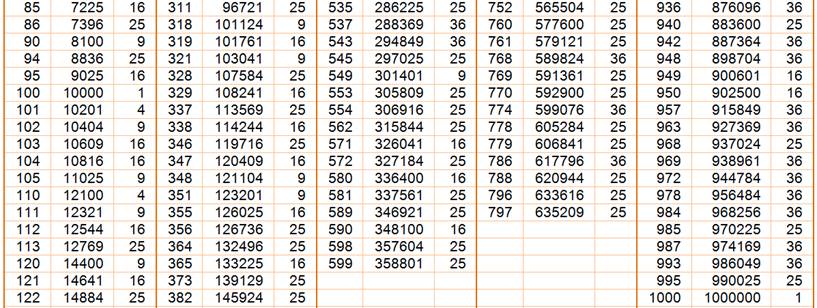
Liste des 253 tels nombres pour n jusqu'à 1 000 Soit 253 / 1000 = 25,3 % par rapport à l'amplitude de n; Soit 250 / 1000 000 = 0,0253 % de doublement carré (N). 169 = 13² est carrément doublement carré: 1 + 6 + 9 = 16 = 4² ; 16 = 4² & 9 = 4² 196 = 14², son permuté, est doublement carré: 1 + 9 + 6 = 16 = 4².

Carré avec somme des chiffres en cube
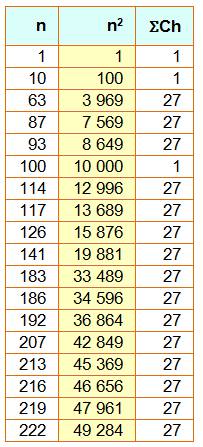
Les premiers exemples de carrés dont la somme des chiffres et un cube. Exemple: 207² = 42 849 et 4 + 2 + 8 + 4 + 9 = 27 = 3^3 Avec pour cet exemple une coquetterie en 2 et 7. Notez: 114 et 141

Suite	Doublement cube Triangulaire carré Carrément carré
Voir	Nombres carrés – Glossaire Nombres carrés – Index Puissance – Index Somme des chiffres à une puissance
Cette page	http://villemin.gerard.free.fr/aNombre/FIGURE/CarDoubl.htm