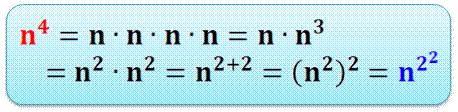|
||||||||||||||||||||||||||||
![]()
|
NOMBRES en PUISSANCE 4 Bicarrés
Note: la dernière égalité est spécifique
à la puissance 2 avec 2+2 = 2x2. |
Anglais: fourth power,
biquadratic number, tessaractic numbers
|
|
||
|
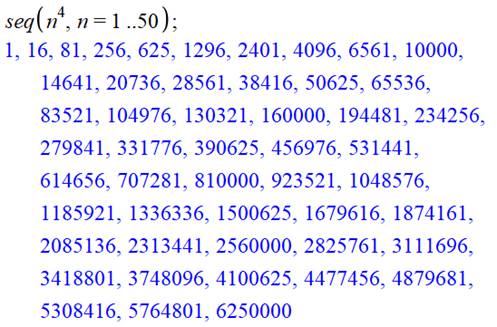
Liste des 50 premières puissances quatrièmes
produites par une simple instruction Maple. |
|
|
Expression complexe d'une puissance
quatrième et calcul de la racine quatrième
|
|
Exemple de calcul (a + ia) (a + ia) (a + ia) (a + ia) = (a² + 2ia² – a²) (a² + 2ia² – a²) = (2ia²) (2ia²) = 4i² a4
= –4a4 |
|
|
Expression des
quatre racines quatrièmes de nombres positifs et négatifs |
|
|
Voir Racines / Formule
de De Moivre
|
|
|
|
Nombres de 1 à 50 ordonnés selon les deux derniers chiffres (dizaines-unités) de leur
puissance quatrième.
|
|
|
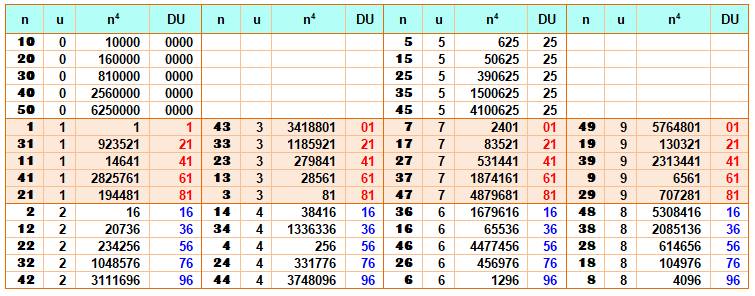
Que
deviennent les milliers, centaines, dizaines et unités (MCDU) de la puissance
quatrième pour l'unité u de n ? u = 0 => MCDU = 0000 u = 5 => MCDU = 0625 u = (1, 3, 7, 9) => DU = (01, 21, 42, 61, 81)
avec U = 1 et D un nombre pair. u = (2, 4, 6, 8) => DU = (16, 36, 56, 76, 96)
avec U = 6 et D un nombre impair. |
|
|
|
||
|
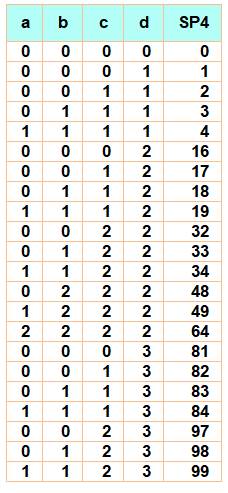
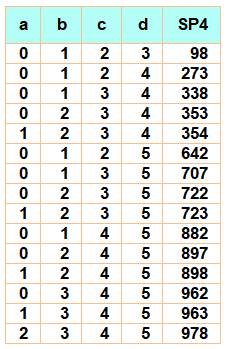
Nombres < 100 somme de quatre bicarrés
|
Nombres < 1000 somme de quatre bicarrés
distincts
Théorème de Waring Tout nombre est somme d'au plus 19 bicarrés. |
|
|
|
||
|
Nombre n4
– 1 pour n de 1 à 15 Identification des plus grands facteurs par ordre croissant: n, n4 – 1, Fle plus grand 1, 0, 0 2, 15, 5 3, 80, 5 4, 255, 17 5, 624, 13 6, 1295, 37 (tous ces
nombres 7, 2400, 5 sont
composés) 8, 4095, 13 9, 6560, 41 10, 9999, 101 11, 14640, 61 12, 20735, 29 13, 28560, 17 14, 38415, 197 15, 50624, 113 Facteur le plus grand dans les nombres n4 – 1
pour n de 1 à 100; liste jusqu'à 100: 0, 5, 13, 17, 19, 23, 29, 37, 41, 53, 61, 67, 71, 73, 89, 97. Rappel: n4
– 1 = (n – 1) (n + 1) (n² + 1) |
Nombre n4
+ 1 pour n de 1 à 15 Identification des plus grands facteurs par ordre croissant: n, n4
1, Fle plus grand 1, 2, 2
Premier 2, 17, 17
Premier 3, 82, 41 4, 257, 257
Premier 5, 626, 313 6, 1297, 1297
Premier 7, 2402, 1201 8, 4097, 241 9, 6562, 193 10, 10001, 137 (le plus petit pour n > 4) 11, 14642, 7321 12, 20737, 233 13, 28562, 14281 14, 38417, 937 15, 50626, 1489 Facteur le plus grand dans les nombres n4 + 1
pour n de 1 à 100; liste jusqu'à 1000: 2, 17, 41, 137, 193, 233, 241, 257, 313, 521, 601,
673, 809, 929, 937. |
|
Puissance 4 et nombres
retournés
|
Puissance
quatrième avec nombres ajoutés à leur retourné. Les seuls
cas possibles, semble-t-il. |
24
= 16 = 8 +
8 54
= 625 = 164
+ 461 = 263
+ 362 114 = 14
641 = 10
340 + 4 301 = 11
330 + 3 311 = 12
320 + 2 321 = 13
310 + 1 331 = 14
300 + 341 |
|
|
||||||
|
Pour s'exercer
|
||||||
|
Pour N = n4 + 4n Le
tableau montre les premières valeurs de cette expression et leur
factorisation. Tous sont composés
avec des facteurs divers. Certes avec souvent 2 ou 5. Mais,
notez le cas de n = 5 avec 1649 = 17 x 97. Dans ces
conditions est-il possible de démontrer que ce nombre est toujours composé. La
première méthode souvent rencontrée sur Internet fait appel au petit
théorème de Fermat en oubliant les cas d'exclusions. La
seconde méthode consiste à trouver une somme de carrés et à la factoriser (identités remarquables). |
n, N, facteurs
|
|||||
|
|
||||||
Voir Même
démonstration
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/PUISSANC/Puissan4.htm
|
![]()