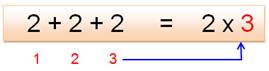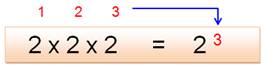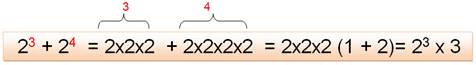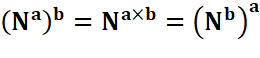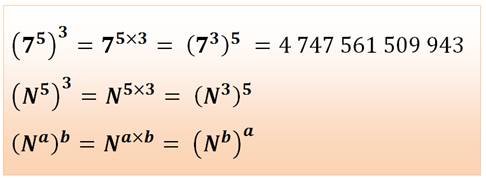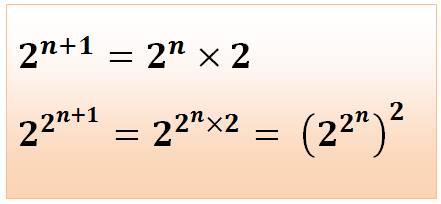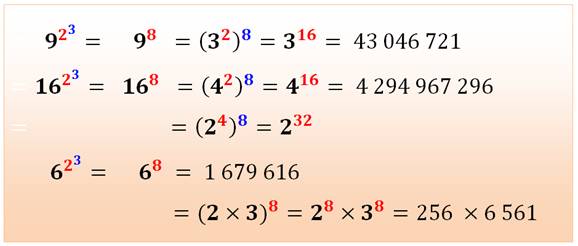|
|||||||||||||||||||||||||||||||||||
![]()
|
Calculs pratiques avec les puissances Rappel sur les puissances;
opérations avec les exposants; et, calculs avec des bases différentes. Toute cette page utilise des
nombres et des calculs numériques. Pour les propriétés générales vues sous la
forme littérale, voir algèbre
des puissances. La manipulation des puissances
nécessite de se souvenir de ce qu'elles signifient et alors tout va bien. |
Voir Brève 52-1031
|
Multiplication |
La
multiplication est une façon abrégée et commode de faire plusieurs fois la
même addition.
|
= 6 |
|
Puissance |
La
puissance est une façon abrégée et commode de faire plusieurs fois la même multiplication.
Cette
opération se lit : deux (à la) puissance trois
égale huit. Le
résultat de l'opération (8) est la puissance. La
quantité de multiplications à effectuer est l'exposant
(3), petit nombre écrit en petit en haut à
droite du nombre. Le nombre (2) porté à une puissance est la base (mot peu utilisé; à ne pas confondre avec base de numération.) |
= 8 |
Voir
DicoMot – Puissance
|
Addition des nombres |
On
se souvient de la signification de la puissance pour réaliser une addition ou
une soustraction. Il n'y a pas de raccourcis de calcul. Cas
d'exposants identiques 23 + 23 = 2x2x2 + 2x2x2 = 2 x 23
= 24 |
8 + 16 = 24 |
|
Multiplication des nombres |
Un
beau raccourci de calcul: Le produit de deux puissances de même base est la somme des exposants. Cas
d'exposants identiques 23 x 23 = 2x2x2 x 2x2x2 = 26 |
= 8 x 16 = 128 |
|
Division des nombres |
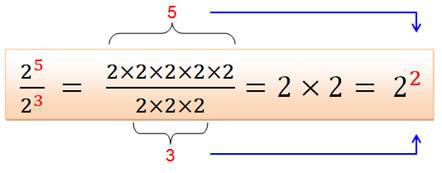
Un
autre beau raccourci: La division des nombres est transformée en une soustraction des
exposants. Cas
d'exposants identiques 23 / 23
= 20 =
2x2x2 / 2x2x2 = 1 |
= 32 / 8 = 4 |
|
20 = 1
21 = 2
|
N0 = 1 N1 = N |
|
2k + 2k
= 2 x 2k = 2k+1 2k x 2k
= 22k =(2k)² |
Nk + Nk
= 2 x Nk Nk x Nk
= N2k = (Nk)² |
|
Addition des exposants |
23 + 2 = 25
= 2x2x2
x 2x2 = 23 x 22 |
= 32 = 8 x 4 |
|
Multiplication des
exposants |
22 x 3 = 26
= 2x2x2
x 2x2x2 = 23 x 23 = (23)2 = 2x2 x 2x2 x 2x2 = 22
x 22 x 22 = (22)3 La multiplication des exposants
correspond au développement d'une puissance à étages
avec parenthèses.
Voir réduction d'un étage |
= 64 = 8 x 8 |
|
Combinaisons |
22 x 3 + 2 = 28
= 2x2x2
x 2x2x2 x 2x2 = 23 x 23
x 22 |
= 256 = 8 x 8 x 4 |
|
Addition |
Calculez
la somme N
= a + b + c avec
a
= 10,45 x 10-12 c
= 72,5 x 10-14 |
J'utilise la même puissance de 10 pour
chacun.
Voir exemple de détail de calcul ci-dessous |
||||||||||||||
|
Changement d'exposant Sans se tromper et, surtout, en
comprenant bien ce que l'on fait. Aucune magie! |
Exemple
avec b. Je
multiplie par une fraction unitaire: 1 =
1012 / 1012. Je
calcule 10-10 x 1012 = 102 En effet, nous avons vu que dans un
produit les exposants s'ajoutent. Je
calcule 0,063 x 100 = 6,3 En effet, le 6 de ce nombre représente bien six centièmes et le 3, trois
millièmes. Je
multiplie par la fraction unitaire: 1 =
10-12 / 10-12 pour obtenir le résultat final. (Cette multiplication se fera désormais mentalement). |
|
||||||||||||||
|
Multiplication & Division |
Calculez
le produit N
= (a x b) / (c x d) avec
a
= 75 x 10-6 c
= 2,5 x 10-4 d
= 0,02 x 10 2 Propriété: Le produit
est commutatif (Ex: 2x 3 = 3 x 2): je peux placer les facteurs où bon me
semble. Note: je sais manipuler
les exposants positifs et négatifs en numérateur comme en dénominateur, en
utilisant par la pensée des fractions unitaires) |
1)
Je m'intéresse d'abord aux nombres: M
= 75 x 21 x 2, 5 x 0,02 = 11, 2875 2)
Puis aux puissances de 10: P = 10-6 x 105
x 104 x 10-2
= 10 -6 + 5 + 4 – 2 = 10 1 = 10 3) Bilan N = M x P = 11, 2875 x 10 N
= 112,875 |
||||||||||||||
|
Changement de base avec des multiples |
43 = 4x4x4 = 2x2 x
2x2 x 2x2 = 26 45 = 4x4x4x4x4 = 2x2
x 2x2 x 2x2 x2x2 x 2x2 = 210 82 = 8x8 = 2x2x2 x
2x2x2 = 26
163 =
16x16x16 = 2x2x2x2 x 2x2x2x2 x 2x2x2x2
= 212 Attention!
Lorsque la base est divisée:
|
|
|
Bases non multiples |
63
= 6x6x6 = 3x3x3 x 2x2x2 = 33 x 23 124 = 12x12x12 =
3x3x3 x 4x4x4 = 33 x 43
= 3x3x3 x 2x2x2 x
2x2x2 = 33
x 26 12n = (3 x 4)n = 3n
x 4n
= 3n x (2x2)n
= 3n x 2n x 2n = 3n x 22n Pour
élever un produit à une puissance, on élève chaque facteur à cette puissance. |
|
|
Opérations |
43 + 82 = 43
+ (2x4)2 = 43
+ 22 x 42 = 43 + 41
x 42 = 43 + 43 = 2 x 43 = 2 x 64 =
128 43 + 82 = (2x2)3
+ (2x2x2)2 = 23x23 + 22x22x22
= 26 + 26 = 27
= 2 x 26 = 21
x 26 = 27 = 128 26
+ 44 + 83 = 26 + (2x2)4
+ (2x2x2)3 = 26 + 24x24 + 23x23x23 = 26 + 28
+ 29 = 26 (1 +
22 + 23)
= 64 x13 Pour calculer
(simplifier) une expression, mettre tout ce qui est possible dans la même base. |
|
|
Simple |
Ce sont les
exposants les plus hauts qui sont calculés les premiers. Notez que la
position des exposants ne peut pas être échangée (commutable). Voyez comme les
exposants du haut sont actifs. |
|
|
|
Bases en 2 et 4 |
En jaune les
formes équivalentes Pas de règle
simple (sauf ci-dessous), mieux vaut développer en
empruntant l'un des chemins indiqués. Attention à la
place des parenthèses et surtout ne pas les éliminer: (2^8)^2 = (256)^2
= 65 536 mais 2^8^2 = 2^(64) =
18 446 744 073 709 551 616 Effet de la priorité
des exposants située le plus en haut. |
||
|
Cas de l'exposant 2 |
Dans le
cas de carrés portés à une puissance, l'exposant de cette puissance croit d'une unité si la base
est portée au carré.
C'est un cas particulier de:
Voir Nombres de Fermat |
||
|
Bases en 3, 6 et 9 |
Voir Puissances à étages |
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()