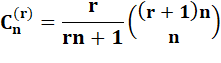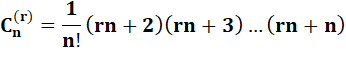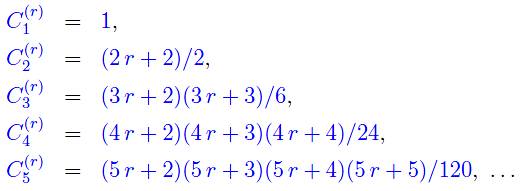Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 11/03/2023 M'écrire Brèves de Maths

INDEX Logique Suites pour dénombrer Dénombrement Jeux et énigmes Vocabulaire des graphes Types de nombres	Dénombrements - MOTIFS
	Nombres de Catalan		Nombres de Naryana		Nombres Manhattan
	Nombres de Catalan – Développements
	Définition	Pascal		Parenthèses		Polygones
	Valeurs	Hipparque		Escaliers		Illustrations
	Fuss-Catalan	Chemins de Dyck		Arbres

Faites un double-clic pour un retour en haut de page

Eugène Catalan

Nombres de Catalan

Constante de Catalan

Conjecture de Catalan

NOMBRES de FUSS-CATALAN Nombres généralisant les nombres d e Catalan et inventés pour dénombres les décompositions de polygones convexes en polygones plus petits.
	Sommaire de cette page >>> Nombres de Fuss-Catalan	Débutants Dénombrement Glossaire Combinatoire

Anglais : Catalan Numbers

Nombres de Fuss-Catalan			haut
Intérêt Utilisés notamment pour la décomposition des polygones dont la triangulation pour r = 1.		Formule
Factorisation
Développement de la formule
Cas de r = 2	1, 3, 12, 55, 273, 1428, 7752, 43263, 246675, 1430715, 8414640, 50067108, 300830572, 1822766520, 11124755664, 68328754959, 422030545335, ….
Polygones	Un nombre Cn(r) est la quantité de manières de décomposer un polygone convexe de rn+2 côtés en polygones de m + 2 côtés portés par des diagonales.

Haut de page (ou double-clic)

Suite	Catalan et parenthèses Catalan et triangle de Pascal Historique des suites de nombres pour compter Nombres de Motzkin Nombres de Genocchi
Voir	Billard Coefficient du binôme Conjecture de Catalan Constante de Catalan Dénombrer – Index Eugène Catalan	Factorielle Méandres Nombres de Bell Premier Sous-factorielles
Sites	Voir Références générales OEIS A001764 – a(n) = binomial(3*n,n)/(2*n+1) (enumerates ternary trees and also noncrossing trees) Multivariate fuss-Catalan numbers - J.-C. Aval Combinatorics of r-Dyck paths, r-Parking functions, and the r-Tamari lattices** – Francois Bergeron
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/Catalan.htm