Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/04/2023 M'écrire Brèves de Maths

INDEX Logique Suites pour dénombrer Dénombrement Jeux et énigmes Vocabulaire des graphes Types de nombres	Dénombrements - MOTIFS
	Nombres de Catalan		Nombres de Naryana		Nombres Manhattan
	Nombres de Catalan – Développements
	Définition	Pascal		Parenthèses		Polygones
	Valeurs	Hipparque		Escaliers		Illustrations
	Fuss-Catalan	Chemins de Dyck		Arbres

Faites un double-clic pour un retour en haut de page

Eugène Catalan

Nombres de Catalan

Constante de Catalan

Conjecture de Catalan

NOMBRES DE CATALAN EXEMPLES Quelques cas d'emploi des nombres de Catalan.
	Sommaire de cette page >>> Cordes et poignées de mains >>> Pile de jetons	Débutants Dénombrement Glossaire Combinatoire

Anglais : Catalan Numbers

Cordes et poignées de mains

haut

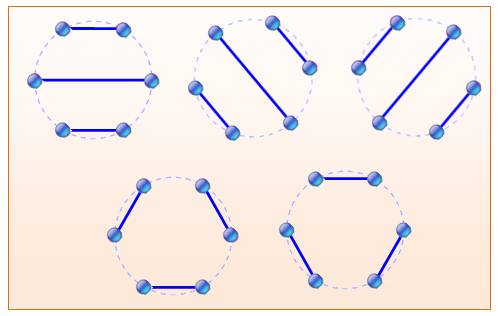
Problème des poignées de mains De combien de façons 2n personnes, disposées autour d'une table ronde, peuvent-elles se serrer la main deux à deux simultanément sans que les mains se croisent ? Poignées de mains et cordes non-sécantes dans un cercle Les points d'un cercle sont connectés par paires en formant des cordes non sécantes. Avec 2n points, la quantité cordes est égale aux nombres de Catalan. 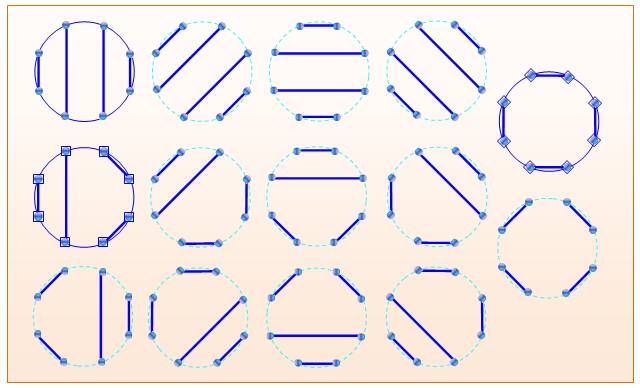5 façons pour 3 paires de poignées de main Les n cordes découpent le disque en n+ 1 régions 14 façons pour 4 paires de poignées de main La majorité des motifs se déduisent par rotations et symétries. Seuls trois motifs sont originaux (cercles pleins). Propriété La quantité de partitions de 2n points en paires non croisées est le nombre de Catalan Cn .

Pile de jetons		haut
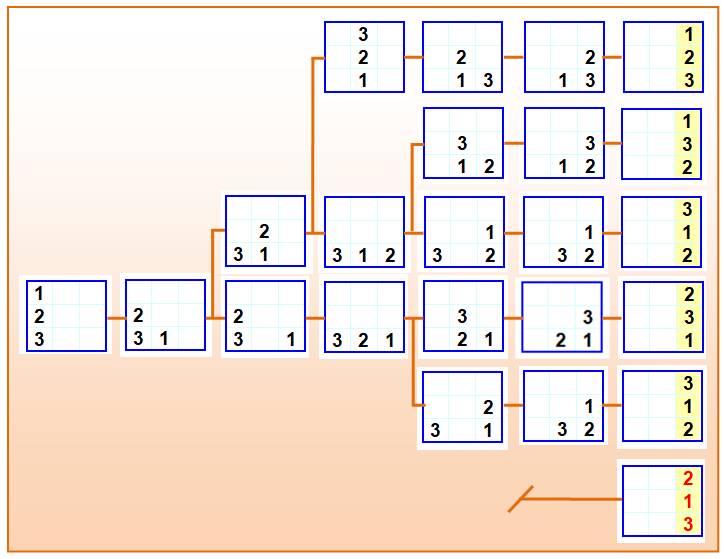
Problème Une pile de jetons dans un plateau. Un jeton à la fois peut passer dans le plateau juste à sa droite. Est-il possible de réaliser les six permutations des nombres 1, 2, 3 ?
Toutes les possibilités de mouvement Il faut six mouvements pour aboutir pour aboutir à la réalisation d'une pile à droite. Il est possible dans réaliser seulement cinq sur les six permutations. Impossible d'avoir la pile 2, 1, 3. Avec n = 3, on obtient 5 permutations = C3; avec n, on aura Cn permutations possibles.

Suite	Chemins de Dyck Catalan et triangle de Pascal Nombres de Motzkin Nombres de Genocchi
Voir	Billard Coefficient du binôme Conjecture de Catalan Constante de Catalan Dénombrer – Index Eugène Catalan	Factorielle Méandres Nombres de Bell Premier Sous-factorielles
Video	Analyse Combinatoire V7 Partitions non croisées
Sites	Voir Références Catalans numbers. What are they and what do they count – Wong Kar Lyle
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/CataIllu.htm