Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 29/03/2023 M'écrire Brèves de Maths

INDEX Arbre Dénombrement Graphe Jeux et énigmes Logique Suites pour dénombrer Topologie	Dénombrements - MOTIFS
	Nombres de Catalan		Nombres de Naryana		Nombres Manhattan
	Nombres de Catalan – Développements
	Définition	Pascal		Parenthèses		Polygones
	Valeurs	Hipparque		Escaliers		Illustrations
	Fuss-Catalan	Chemins de Dyck		Arbres – Catalan

Faites un double-clic pour un retour en haut de page

Eugène Catalan

Nombres de Catalan

Constante de Catalan

Conjecture de Catalan

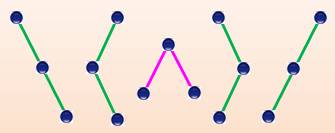
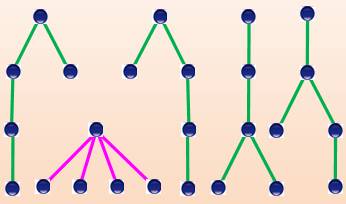
Arbres-Catalan pour n = 3		haut
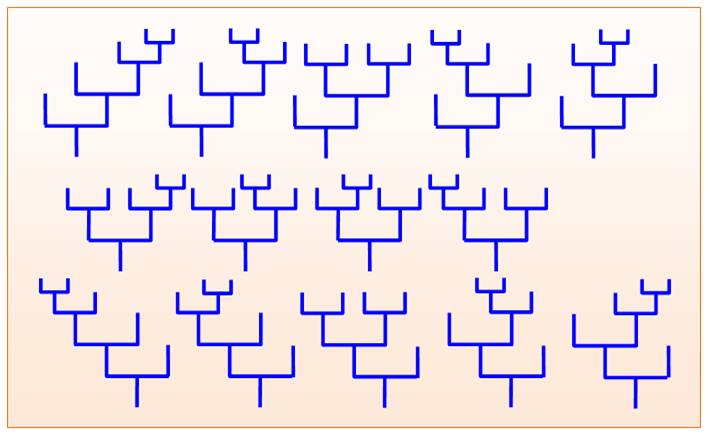
Pour chacun de ces types d'arbres avec n = 3, on a:	Quantité d'arbres: C3 = 5 Avec n = 4, on aurait: C4 = 14 arbres.
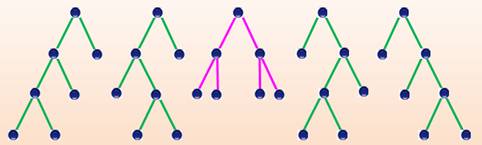
Arbre binaire
Arbre binaire plan avec 2n+ 1 sommets (ou n+1 extrémités)
Arbre plan à n+1 sommets
Arbres plan enracinés à 2n+ 2 sommets
Arbres plan à n+2 sommets tels que le chemin de droite ait une longueur impaire

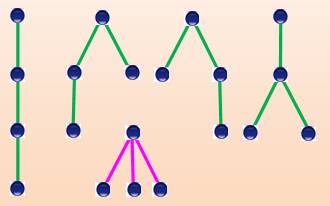
D'après: Stanley

Les quatorze arbres avec tronc et à 5 feuilles

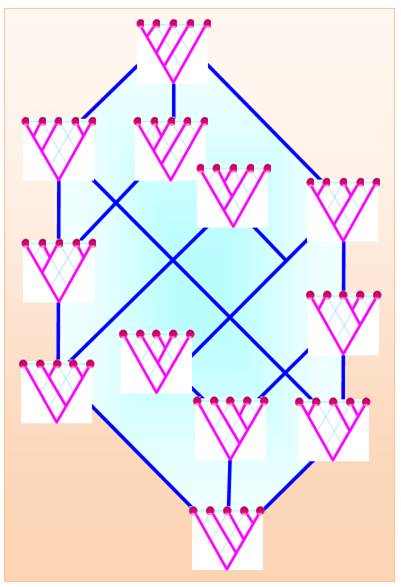
Voir Nombre 14 dans le DicoNombre

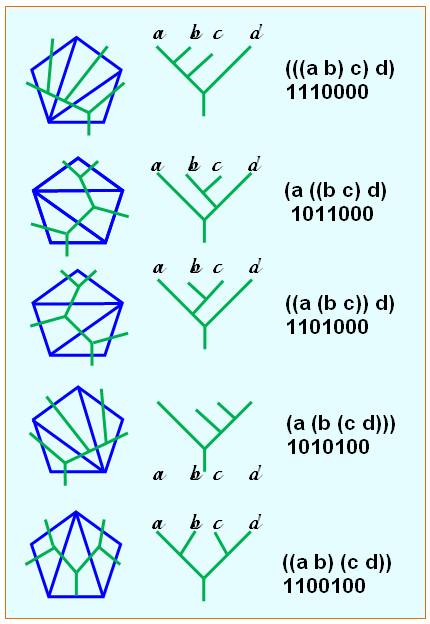
Correspondance avec la triangulation des polygones Exemple avec l'hexagone: Ce polygone étant découpé en triangles, on dessine un arbre dont les branches coupent chacun des segments (tracé vert dans le polygone). Cet arbre est redressé tel que montré en colonne centrale, et il porte les branches d'extrémités nommés a, b, c et d. La correspondance avec la mise en parenthèse figure en colonne de droite, ainsi que le code du motif. C'est Arthur Cayley qui le premier proposa la représentation en arbres à tronc unique (un vrai arbre) et trivalents (trois fourches)

Voir Exemple de correspondance arbre polygone

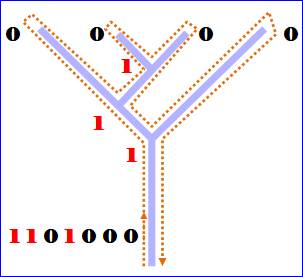
Codage appliqué à l'arbre

Lire les valeurs 0, 1 en suivant le chemin de contournement

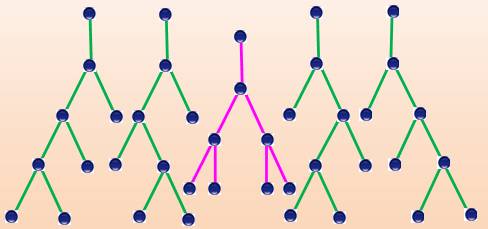
Les quatorze arbres trivalents à tronc et à 5 feuilles (extrémités)

Quatre formes en U => C₄ = 14

Suite	Arbres simples – Introduction aux arbres Arbres de distribution Catalan et parenthèses Catalan et triangle de Pascal Historique des suites de nombres pour compter Nombres de Motzkin Nombres de Genocchi
Voir	Billard Coefficient du binôme Conjecture de Catalan Constante de Catalan Dénombrer – Index Eugène Catalan	Factorielle Méandres Nombres de Bell Premier Sous-factorielles
Sites	Voir Références Catalan Arbre (théorie des graphes) – Wikipédia Binary Tree Data Structure – Geeksforgeeks – Description et programmation en C++ Formule de Cayley – Wikipédia OEIS A000272 – Number of trees on n labeled nodes: n^(n-2) with a(0)=1 Cayley Tree – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/Arbres.htm