Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 29/12/2022 M'écrire Brèves de Maths

INDEX Nombre et facteurs Types de nombres	Types de Nombres – Diviseurs
	Parfaits	Semi-parfaits (SP)	SP Primitifs	SP Primaire
	Refactorisables	Pratiques	Abondant primitifs	Friables
	Facteurs-Diviseurs	Intouchables	Lucas-Carmichael	Pierpont
	Petits facteurs	Somme-Facteurs

Nombres à petits facteurs Les nombres dont le plus grand facteur est petit par rapport au nombre. Exemple: 324 = 2^2 · 3^4 et R = 3 / 324 = 0,926 % Le plus grand facteur de 324 représente moins de 1% de ce nombre. Aussi, les nombres dont le radical (produit des facteurs) est petit par rapport au nombre. Exemple: 18 = 2 ·3² et R = 6 / 18 = 33,3 %
	Sommaire de cette page >>> Approche >>> Nombres à petits facteurs avec R < 1% >>> Nombres à petits facteurs – RECORDS >>> Nombres à petit radical – RECORDS	Débutants Nombres Glossaire Nombres

Nombres ronds de Hardy (1999)

Nombre composé de beaucoup de petits facteurs premiers.

1200 = 2⁴ x 3 x 5² est un nombre rond. Son plus grand facteur (5) représente 0,42 % de sa taille.

Hardy énonce que les nombres ronds sont rares. Cet adjectif, dans ces circonstances, a été vite abandonné. On a parlé de nombres sans grands facteurs premiers ou de nombres lisses (smooth numbers) pour arriver à se stabiliser sur nombres friables (friable numbers).

Leur étude par Hardy en coopération avec Ramanujan (1917), fut le point de départ à l'évaluation statistique de la quantité de facteurs premiers d'un nombre entier.

La théorie des entiers sans grands facteurs premiers s'est ensuite développée, notamment pour la cryptographie. Cette discipline appartenant à la théorie algorithmique des nombres, exige au contraire des nombres avec facteurs de grande taille.

Suite en nombres friables

Approche		haut
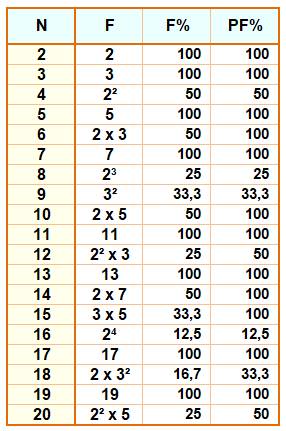
Le nombre 6 est égal = 2 x 3. Le rapport F% de son plus grand facteur 3 sur le nombre lui-même vaut 3 / 6 = 50% Le rapport PF% du produit de ses facteurs (radical) sur le nombre lui-même vaut 6 / 6 = 100% L'étude des nombres à petits facteurs s'intéressé à de plus grand nombres, nombres pour lesquels le rapport devient petit. Inférieur à 1% par exemple. Ou, aux nombres successifs pour lesquels le rapport diminue (record).

Nombres à petits facteurs avec R < 1%		haut
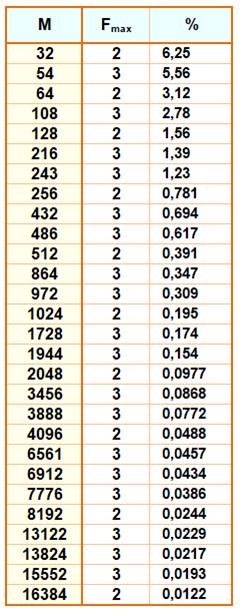
Les nombres ayant un rapport F% (plus grand facteur / nombre) inférieur à 1%. Ils sont 33 jusqu'à 1000. Le plus petit nombre de rapport inférieur à 1% est 256, une puissance de 2.

Nombres à petits facteurs – RECORDS		haut
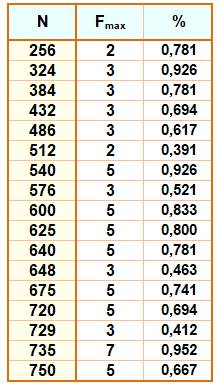
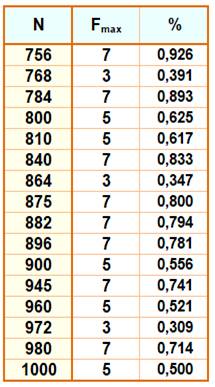
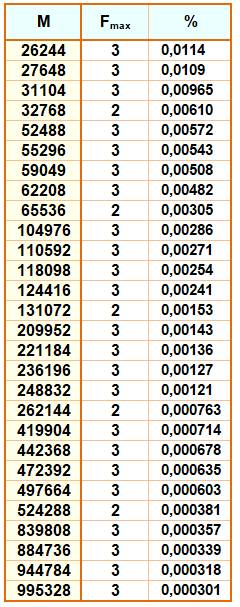
Les nombres ayant un rapport F% record. Le rapport du suivant est inférieur au précédent dans la liste. Ils sont 61 jusqu'à 1 million. Les plus petits records Ici, il s'agit du rapport entre le facteur le plus grand et le nombre, ce facteur étant unique même s'il est porté à une puissance.

Nombres à petit radical – RECORDS		haut
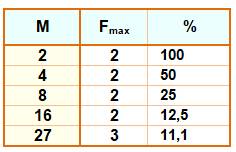
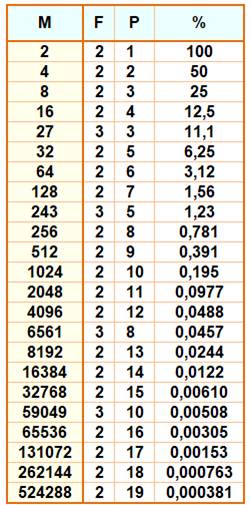
Les nombres ayant un rapport PF% record (rapport entre le radical et le nombre). Le rapport du suivant est inférieur au précédent dans la liste. Ils sont 23 jusqu'à 1 million. Ces records sont un sous ensemble de la table des records en facteur le plus grand (ci-dessus). Ce ne sont que des puissances de 2 ou de 3.

Haut de page

Retour	Nombres friables
Suite	Abondant primitifs Facteurs-Diviseurs
Voir	Facteurs et diviseurs Diagramme de Venn Diagramme de Karnaugh
DicoNombre	Nombre 256 Nombre 323 Nombre 735
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/PtFacteu.htm