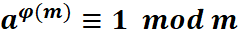NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CODAGE
Débutants Général	Cryptologie			Glossaire Chiffre
INDEX Cryptologie Théorie des nombres	Cryptologie	Décalage lettres	Clé publique	RSA
		Codage	Bureau 47	Nombres RSA
		Message	Sécurité	Pig Pen
		Übchi	LLL	Nombres
		Sommaire de cette page >>> Bases >>> Exemple >>> Théorie >>> Extension

CHIFFREMENT RSA

ou codage ou cryptage RSA

Chiffrement à clé asymétrique.

Pourquoi c'est sûr? Pour deux raisons au moins:

Utilisation d'une fonction non réversible qui repose sur les propriétés de l'arithmétique modulaire

Difficulté à factoriser les grands nombres

Voir principes en Clé publique / Historique

Inventeurs

R	S	A
Ronald Rivest É.-U. né en 1947	Adi Shamir Israël né en 1952	Leonard Adleman É.-U. né en 1945

BASES
Tu veux me transmettre la valeur x. Je te transmets sans précaution la clé publique (e et n). Tu t'en sers pour crypter le message. Tu me le transmets: y Je suis le seul à pouvoir décrypter car j'ai la clé privée.
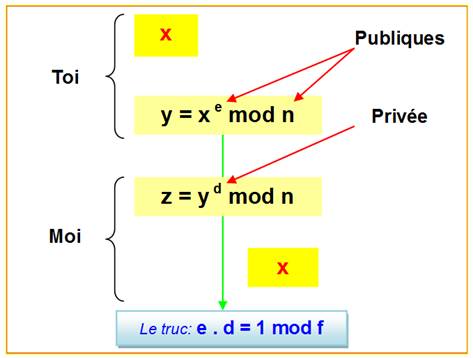
	x est la valeur que tu veux coder (tu découpes le message de façon que x < n). e et n sont les deux éléments de la clé publique. Tu enfouis x dans un calcul qui donne y. y est la valeur transmise. Je calcule z en utilisant ma clé privé d. Après ce tour de passe-passe mathématique, il se trouve que z est égal à x.
En effet z = y^d mod n (x^e mod f)^d mod n x^ed mod n x^1 mod n x	Voici le calcul La justification précise est un peu plus compliquée. Tout tient dans le choix de e et f. Voir l'exemple ci-dessous.

Voir Théorie du modulo

EXEMPLE
Ma sauce à moi (préparation des clés)
Deux nombres premiers tenus secrets	p et q	3 et 7
Son produit n est diffusé	n = p.q	n = 21
On calcule f	f = (p – 1) (q – 1)	f = 2x6 = 12
Un nombre e est, lui aussi, diffusé	e premier avec f	e = 5
Je calcule d, inverse de e mod f	e.d = 1 mod f	5d = 1 mod 12 5x5 = 1 mod 12 d = 5
Préparation du message
Le message est converti en chiffres On va coder chaque chiffre	x1 … xi … avec xi < n	x = 2, par exemple
Codage du message
Chaque x est codé par y	y = x^e mod n	y = 2^5 mod 21 y = 32 mod 21 y = 11
Les valeurs de y sont transmises	y est transmis	11 est transmis
Déchiffrage
Je calcule z	z = y^d mod n	z = 11^5 mod 21 z = 11 x121x121 mod 21 z = 11 x 16 x 16 mod 21 z = 11 x 256 mod 21 z = 11 x 4 mod 21 z = 44 mod 21 z = 2 mod 21
Car en fait	z = x mod n	z = 2 mod 21

THÉORIE

Quelques rappels théoriques

La fonction phi (n) : est la quantité d'entiers strictement positifs inférieurs à n et premier avec n.

Théorème de Fermat-Euler

Si a est premier avec m, alors

La notation ci-dessus est la plus formelle; on peut se permettre de simplifier lorsqu'il n'y a pas confusion. Ce sera le cas ci-dessous.

La démonstration ci-dessous est valable pour le cas général où x est premier avec n. On peut montrer que le procédé reste valable même dans les autres cas.

RSA - Raisonnement

Il s'agit de prouver le raisonnement suivant:

z =	y^d mod n x^ed mod n x

Quelques calculs préalables

On se souvient que

f =

(p – 1) (q – 1)

C'est l'indicateur d'Euler ou fonction phi de n

f =

(n)

On a également

e.d=

=

1 mod f

1 mod (n)

Ce qui veut dire que e.d – 1 est un multiple de phi

e.d – 1 =

k . (n)

Expression de z

Si on revient à z

z =

y ^d mod n

(x ^e ) ^d mod n

x ^{e . d} mod n

On ajoute un facteur en x que l'on retire dans l'exposant

z =

x . x ^{e . d - 1} mod n

On connaît la valeur de cet exposant

z =

Il est temps d'appliquer le théorème de Fermat-Euler

z =

x . (1) mod n

x . mod n

Or on a choisit x < n

z =

x

Extension
Merci à Pierre Noël pour cette démonstration

Suite	Nombres RSA Algorithme LLL Voir haut de page
Voir	Autocodes Cadenas Clés de cryptage Codage décimal Codage des lettres Codage RSA Code barre Code ISBN des livres Cryptogrammes Message chiffré Théorie des nombres
Livres	Le vol du frelon – Ken Follet – Robert Laffont – 2003 – page 92 La conjecture de Fermat – Jean d'Aillon – JC Lattès – 2006 Dossier Pour La Science spécial "La cryptographie - l'art du secret" - juillet 2002
Cette page	http://villemin.gerard.free.fr/Crypto/RSA.htm