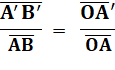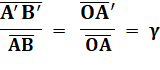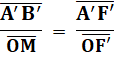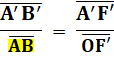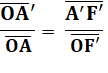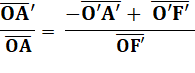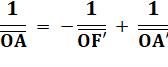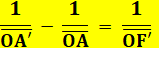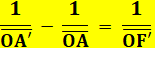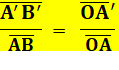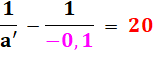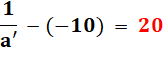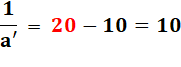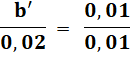|
||||||||||||||||||||||||||||
![]()
|
Les lentilles convergentes Élèves Le prof n'a pas expliqué ce
qu'est un foyer. Je ne vois toujours pas
ce que c'est pour une lentille. La distance
focale c'est quoi et la dioptrie
affublée d'un signe cabalistique, je n'y comprends rien. Le prof utilise deux formules et trouvent des résultats en pratiquant
des tours de passe-passe. J'essaie de l'imiter et ne trouve jamais les mêmes
résultats. Il nous parle de grossissement. Je ne comprends pas du tout d'où
cela vient. Auteur du site Un flot d'incompréhensions
que j'ai pu constatées auprès d'élèves pourtant assez doués. Voici quelques
explications pour palier les manques sans doute dus à l'insuffisance de temps
passé en classe. |
|
|
|
|
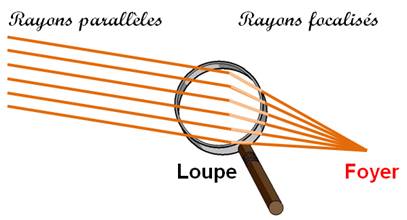
Dans Tintin au Congo, le petit reporter perché sur une branche fait
fuir l'éléphant en lui grillant la couenne à l'aide d'une loupe. La loupe
apparaît également dans le secret de la Licorne. L'un des Dupont s'y grille
le derrière par inadvertance.
L'intérieur de la pipe, là où est déposé le tabac, s'appelle le foyer ou le fourneau. Définition du foyer, là où
on fait du feu; de l’adjectif latin focarius signifiant: de feu. |
|
|
|
|
|
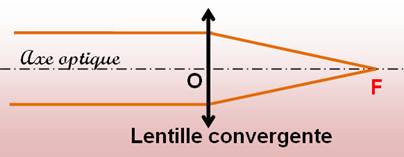
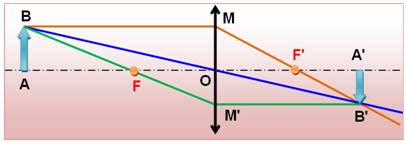
Représentation schématique
|
|
C'est quoi le FOYER? Là où ça converge?
|
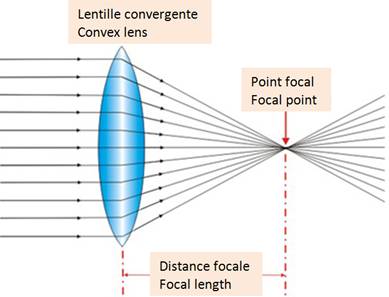
Oui, il est possible d'expliquer le phénomène de convergence.
Il faudrait tracer le trajet des rayons soumis à la diffraction
en entrant et en sortant de la lentille. Au lycée, on se contente de savoir
que, comme on le constate avec la loupe, il existe un point spécifique de
convergence des rayons. Pour obtenir
une image nette, vous avez déjà constaté qu'il faut tenir la loupe à une
distance précise, sinon l'image est floue. Prenez une loupe à fort
grossissement et observez une image en couleur dans un magazine. L'image est
faite de petits points de couleur. Vous expliquerez cette technique plus tard
dans le cours en étudiant la trichromie. |
|
|
||
|
|
|
|
|
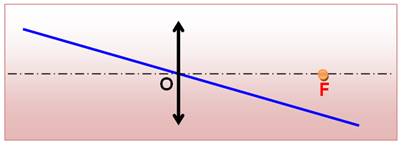
Règle 1
C'est exactement ce que nous avons vu plus haut avec la loupe. |
|
|
|
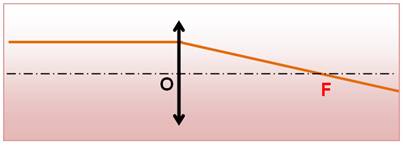
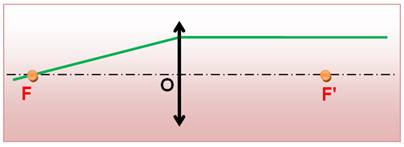
Règle 2
Le centre optique est neutre pour les rayons. |
|
|
|
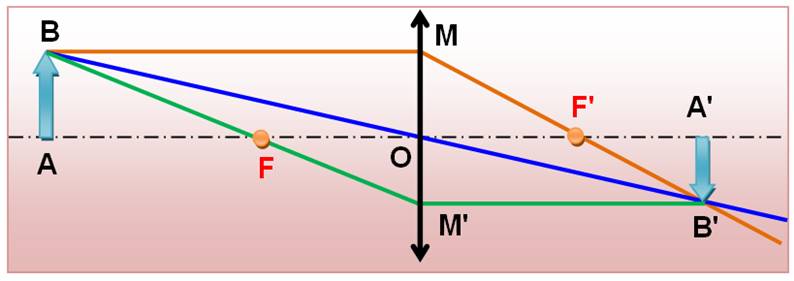
Règle 3
La lentille étant symétrique, il n'y a pas de raison que les
situations, en haut et bas, ne soient pas symétriques. |
Baptême des deux points focaux: F est le point focal objet et F' (F prime) est le point focal image.
Tout ce qui aura trait à l'image sera nommé avec le "prime". |
|
|
|
|
|
Le rapport de taille
entre l'image et l'objet est dans la même proportion que les distances de
l'image et de l'objet au centre optique. Note: la barre
sur les noms des segments signifie simplement que l'on s'intéresse à
l'orientation, au signe. Une longueur sera
positive vers la droite ou vers le haut; négative vers la gauche ou vers le
bas. Comme sur un repère classique en maths.
|
|
Grandissement
|
La formule que nous venons de trouver le plus
simplement du monde est l'une des deux formules à connaître. Elle témoigne du
grossissement ou rapetissement de l'image par rapport à l'objet. C'est le grandissement parfois baptisé par la lettre
grecque gamma.
|
|
|
|
|
|
|
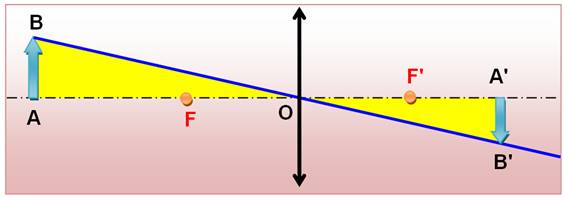
Écran total
|
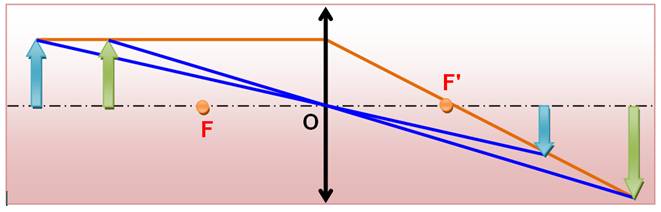
Si l'objet est placé en arrière du foyer objet,
alors l'image se forme de l'autre côté de la lentille. Elle est réelle au
sens où vous pouvez l'observez en plaçant un écran
au foyer image. En rapprochant l'objet du foyer, il faut placer l'écran de
plus en plus loin de la lentille; l'image s'enfuit au loin.
En arrivant au foyer objet, l'image est à l'infini
(rayons marron et bleu parallèles). En dépassant ce point, l'image revient par
derrière (à gauche) sous forme virtuelle, impossible à matérialiser sur un
écran. |
|
|
||
|
|
|
|
|
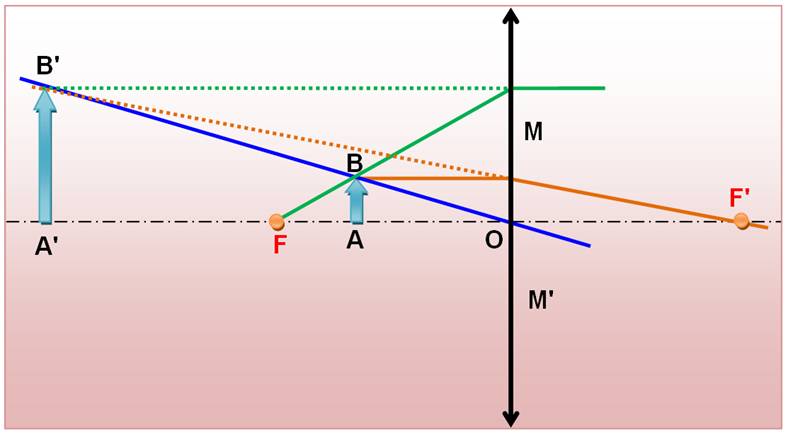
Prenons les triangles
rectangles, ayant leurs angles égaux. |
A'B'F' & OMF' semblables |
|
|
Proportionnalité selon
Thales. |
|
|
|
Par construction de la parallèle. |
|
|
|
Remplacement. |
|
|
|
Rapprochement avec notre
première formel de grandissement. |
|
|
|
Nouvelle identité |
|
|
|
Évaluation de A'F' avec la relation de
Chasles (simple, ici) |
|
|
|
Remplacement. |
|
|
|
Produit en croix. |
|
|
|
Division par OA.OA'.OF' |
|
|
|
Mise en forme sympathique. |
|
|
Association ou conjugaison des foyers
|
Cette identité est connue sous le nom de relation de conjugaison de Descartes. Conjugaison parce qu'elle
associe de façon symétrique, les positions de A et A'. En maths un conjugué et une sorte de
frère jumeau. Et cette conjugaison est fonction de l'inverse de la distance
focale. Pour des raisons purement pratique, les physiciens, ont donné une
nouvelle unité: la dioptrie. Pas de panique! La dioptrie
est un autre nom de l'inverse des mètres, symbolisé par la lettre grecque
delta. Cette grandeur est aussi nommée la vergence
(V) de la lentille.
|
|
|
||
|
|
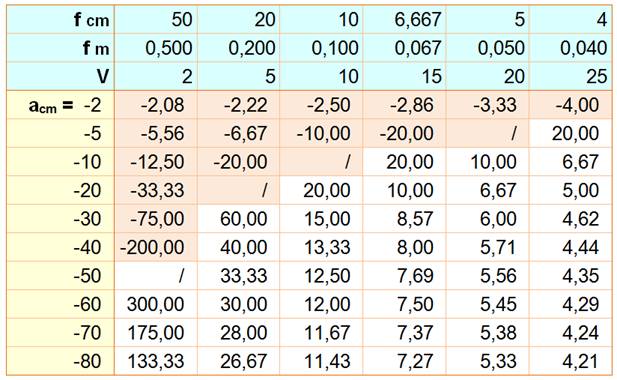
Objet de 2 cm à 10 cm
du centre optique. |
|
|
|
Distance au centre optique
de l'image: a'. Taille de l'image: b'. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Avec a distance à l'objet et a' celle de l'image;
b
la taille de l'objet et b' celle de l'image.
Ce tableau donne la valeur de a' en fonction de a
et de la vergence V
Exemple: avec a = -40 cm et V = 15
on vérifie: 1/0,08 - 1/-0,4 = 12, 5 + 2, 5 = 15 |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/OPTIQUE/Lentille.htm |
![]()