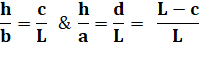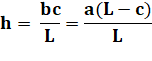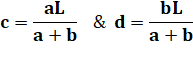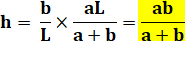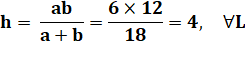|
||||||||||||||||||||
![]()
|
THALÈS de MILET
Autour
de 600 av. J.-C.
Mathématicien Physicien Philosophe
Thalès,
Pittacus, Bias, Solon, Cléobule, Myson, Chilon
|
Anglais
: THALES OF
|
625 / 547 av. J.-C . / 78 ans Certains disent
640 pour la naissance |
|
|
-
met sa fortune au service de ses envies en se retirant des
affaires pour se consacrer aux études et aux voyages.
-
Utilise pour la première fois les démonstrations
déductives. -
Il ouvre la voie aux grandes découvertes des pythagoriciens, puis aux Éléments
d'Euclide.
-
Il fait passer du stade de l'observation et de
l'expérience à celui de la méthode et de la théorie:
|
|
|
Un peu plus de détails |
|
|
THALÈS
-
en particulier: l'astronomie -
et se taille une jolie réputation en rentrant au pays.
-
Hérodote raconte qu'elle survint au cours d'une
bataille. -
Elle a pour effet de stopper les combats. -
Et d'installer la paix pour longtemps. Thalès n'a certainement pas pu prévoir
l'éclipse par calcul des mouvements des astres. Sans doute connaissait-il le saros,
période moyenne de répétition des éclipses.
-
Lesquels savent construire des pyramides
(depuis déjà 1500 ans). -
Thalès les bluffent en donnant la hauteur de la grande pyramide. -
Il utilise les propriétés des triangles
semblables. -
qui deviendra le théorème de Thalès
(nom donné au 18e siècle).
-
Il fait partie des Sept Sages désignés par ses
contemporains.
-
Il démontre des théorèmes qu'Euclide reprendra par la
suite. -
En introduisant des règes de déduction logique. -
Pour nommer cette science, il conserve le vocable
égyptien de "mesure de la Terre" mais le traduit en grec: géométrie.
-
qu'un diamètre
partage un cercle
en deux demi-cercles superposables; -
que les angles à
la base d'un triangle
isocèle sont superposables; -
que tout angle inscrit dans un demi-cercle est un angle
droit; -
etc.
-
L'égalité des nombres
est connue, mis Thalès l'étend à la géométrie. -
Deux figures sont égales (congrues) si en les faisant
glisser et pivoter, il est possible de les superposer.
-
Toute la matière
doit être fondamentalement la même: l'eau.
L'eau se transforme en solide ou en gaz; la nourriture contient généralement
de l'eau; etc. -
Anaximandre, son étudiant, pense que l'humain descend
du poisson. -
Thalès pensait que la matière pouvait être
théoriquement divisée indéfiniment (en entités continues de plus en plus
petites). Il se trompait. Démocrite avait raison avec ses atomes. -
Thalès montre que l'ambre (résine nommé elektron par
les Grecs) une fois frottée est capable d'attire des plumes d'oiseau.
-
La Terre est
sphérique déduction faite à partir de l'observation de l'ombre de la Terre
sur la Lune. -
L'orbite apparente du Soleil
est inclinée par rapport a plan de l'équateur. |
|
|
Contemporains
de Thalès
-
Thalès le rencontrera à la fin de sa vie. -
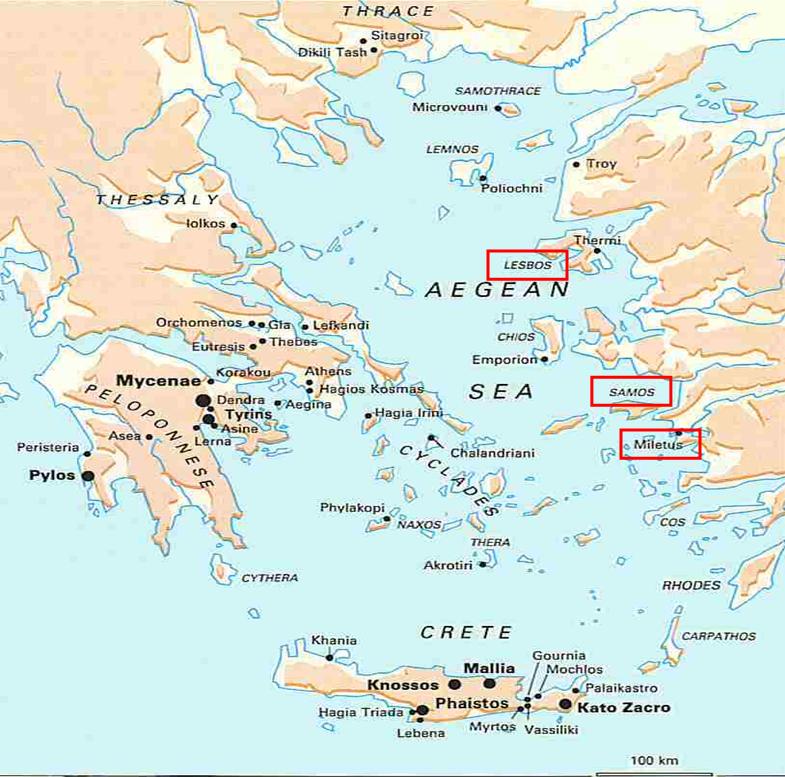
Pythagore est de Samos
et Thalès de Milet, deux îles voisines. -
Avant de se rendre à Milet et rencontrer Thalès,
Pythagore s'est arrêté à Lesbos, une autre île
du coin (origine du mot lesbienne). |
|
Voir Contemporains
À noter
|
En France, le théorème de Thales
se rapporte aux proportions découpées par des sécantes sur des parallèles. En
anglais, il se nomme parfois Thales theorem, mais plutôt: Intercept theorem. En Anglais, le Thales theorem
dit que l'angle inscrit dans un cercle
interceptant un diamètre est un angle droit. >>>
|
![]()
|
|
||
|
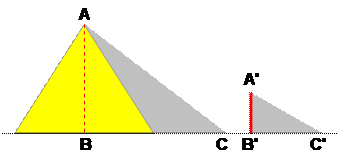
CAS
DU TRIANGLE
Les droites rouges sont parallèles. Autre formulation
Réciproquement, si ces rapports existent, les droites
rouges sont parallèles. |
Notez: en combinant les deux relations citées à gauche:
|
|
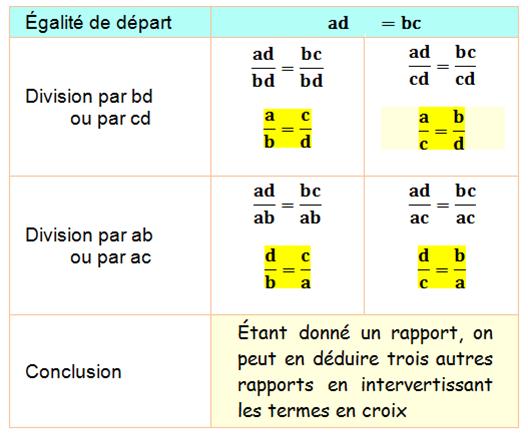
Rappel sur le calcul de rapports
|
a, b, c et
non nuls évidemment ! |
|
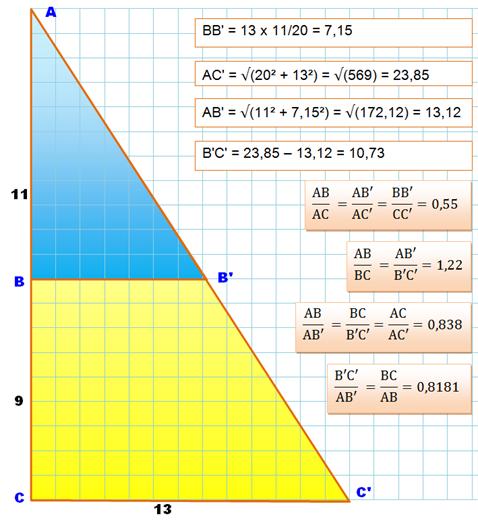
Calcul des rapports sur un exemple simple Une des sécantes est perpendiculaire aux
deux droites parallèles, formant des triangles rectangles. On calcule les rapports indiqués ci-dessus
et on vérifie le théorème de Thales sous tous ces rapports. Note: le calcul de la longueur de BB'
utilise le théorème de Thalès; on aurait tout aussi bien pu le mesurer pour
que la vérification soit pertinente jusqu'au bout. |
|
|
Théorème
de Thalès – CAS GÉNÉRAL
Attention
et BB'/CC' varie.
|
|
|||||
|
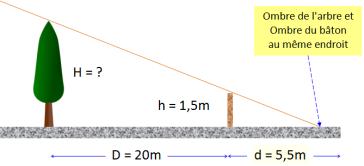
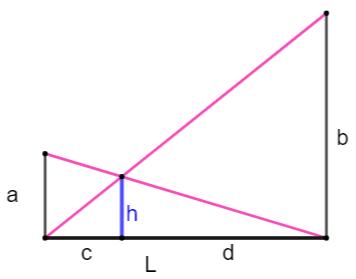
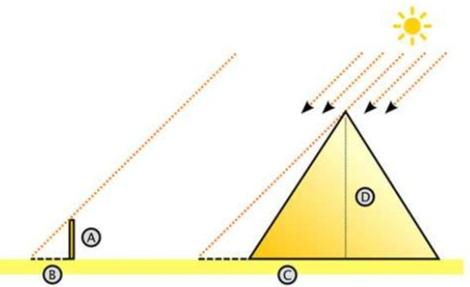
Exemple
classique
-
L'arbre (réduit à une droite passant par le sommet et
le tronc) et le bâton sont les côté parallèles de deux triangles rectangles. -
Ces deux triangles rectangles ont un angle commun
(extrémité à droite). -
Ils sont semblables. (l'un se
déduit de l'autre par un effet de zoom).Nous pouvons appliquer le théorème de
Thalès qui dit que les mesures de l'un et de l'autre sont proportionnelles
(dans le même rapport). |
Les
côtés verticaux sont dans la même proportion que les côtés horizontaux.
H = 25,5 x 1,5 / 5, 5 = 6,95 m |
Voir Hauteur de la pyramide de Khéops
(Thalès) / Hauteur du
donjon (loi des sinus)
|
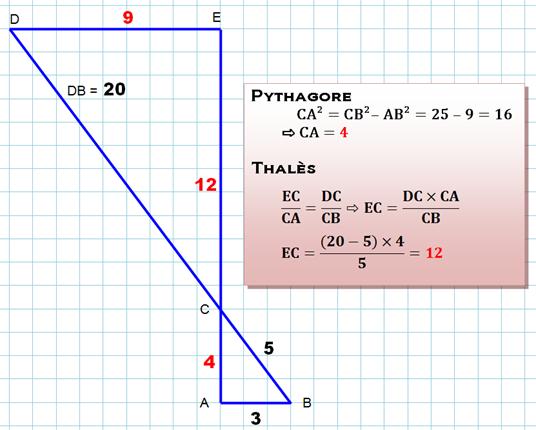
Mariage entre Thalès et Pythagore Sur cette figure AB, BC et BD sont connues
(noirs). Donner les mesures de AC et AE (rouge).
On
trouvera la mesure de DE avec Pythagore:
DE² = 15² – 12² = 81 = 9² |
Voir Construction
de 1/a / Théorème de la
bissectrice / Doubler le triangle rectangle /
Théorème du point
milieu / Théorème de Pythagore
|
|
||
|
Problème Sur cette
figure, on mesure: Solution La
longueur de base L peut être quelconque ! Calculs avec le théorème de Thalès
bc = aL – ac
|
Figure
Exemple
Triplets entiers pour (a, b, c) [3, 6, 2], [4, 12, 3], [5,
20, 4], [6, 12, 4], [6, 30, 5], [8, 24, 6], [9, 18, 6], [10, 15, 6], [12, 24,
8], [15, 30, 10], [20, 30, 12], [21, 28, 12], … |
|
Voir Brève
647
|
|
||||||||
|
|
|
|||||||
|
D = A · C / B (C = ombre + ½ base de la pyramide) |
|
|||||||
Explications du calcul >>> / Quelle est la hauteur de l'immeuble?
Voir
illustration et complément sur le site de Serge Mehl
|
|
|
|
La société
d'électronique professionnelle Thomson-CSF est devenu THALES en
décembre 2000:
Elle a une réputation internationale
dans les domaines des systèmes aéronautiques, des systèmes de défense, des systèmes de sécurité, des grands réseaux critiques, etc.
-
Satellites
(Thales Alenia Space), -
Équipements de bord des avions, -
Systèmes de contrôle de trafic aérien, -
Simulateurs d'entraînement, -
Systèmes d'informations, -
Systèmes de sécurité et de sûreté,
-
Protection de l'environnement, -
Etc.
-
Systèmes de commandement, -
Systèmes de défense des bâtiments
de surface, des sous-marins,
des avions, des hélicoptères … -
Radars, sonars,
périscopes … -
Communication et télécommunications, -
Etc. |
|
Voir le site du GROUPE THALES / CV
de Gérard Villemin / TUS à
Sophia Antipolis
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette Page |
![]()