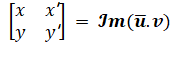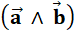Glossaire Vecteur

VECTEUR

Sur cette page

>>> Vecteur – Approche et définition

>>> Vecteur – Propriétés

>>> Anglais

>>> Relation de Chasles

>>> Produit scalaire

>>> Produit vectoriel et produit mixte

>>> En savoir plus

Approche

Comment représenter:

- la direction du Nord,

- le poids de mon cartable qui pèse sur mes épaules,

- la force que j'exerce quand je tire sur mon bagage à roulettes,

- la vitesse de la voiture en ligne droite ou lorsque je vire,

- la direction du Nord, ou plus exactement, l'intensité de l'attraction du pôle nord magnétique,

- etc.

Une flèche plus ou moins longue fera l'affaire :

- elle donne la direction, le sens ;

- sa longueur témoigne du degré de force, de puissance …

Voir Vecteurs – Une approche pour débutants

Définition

Vecteur: segment de droite orienté qui représente une grandeur, comme une force, une vitesse, un champ …
Le vecteur est représenté par un segment fléché ().

Vecteur lié: dont l'origine est un point bien précis; synonyme de bipoint.

Vecteur libre: dont l'origine n'est pas fixée; représente toute la classe des vecteurs qui lui seraient équipollents.

Le nom vecteur vient du latin vector, celui qui transporte; passager d'un navire, cavalier; le verbe étant veho transporter.

Vocabulaire

Norme: sa longueur, notée

Vecteur unitaire: sa norme est égale à 1.

Direction: celle de la droite portant le vecteur.

Sens: orientation de la droite.

Quadrivecteur ou tétravecteur: vecteur à quatre composantes utilisé en théorie de la relativité.

Précision de vocabulaire

Un "vecteur" pris individuellement est appelé: bipoint.

Un vecteur est une classe d'équivalence de bipoints équipollents.

Ce qui veut dire:

équipollent: tous les mêmes par translation (voir ci-dessous).

classe d'équivalence: une famille

Traduction: un vecteur est en fait toute la famille des bipoints translatés.
On représente un vecteur par l'un quelconque de ses bipoints.

Propriétés

ÉGALITÉ

- si les deux vecteurs ont même direction et même sens et si les longueurs AB et CD sont égales, ou

- si ABDC est un parallélogramme, ou

- si les segment [AB] et[CD] ont même milieu, ou

- si CD est un vecteur obtenu à partir du vecteur AB par translation

On dit que les deux vecteurs sont égaux ou équipollents

Définition: deux vecteurs sont équipollents si et seulement si les segments AD et CB ont même milieu. Les points ABDC forment un parallélogramme. Les droites (AB) et (CD) sont parallèles et IJ = LK.

Opérations

ADDITION de vecteurs

- Vecteurs bouts à bouts
Relation de Chasles

Voir Explication et exemple

- Vecteurs avec même origine Règle du parallélogramme

Voir Addition de complexes /

Angles orientés

Addition dans le plan

=> parallélogramme

Addition dans l'espace

=> parallélépipède

MULTIPLICATION par un réel

- Vecteur et un nombre réel non nul, le vecteur est tel que =>

- Si alors les points A, B et C sont alignés.

Norme =

Direction de

Sens de si

Sens contraire de si

Milieu

- Segment [AB] et
I le point milieu de AB,
alors =>

Coordonnées

Polaires

Cartésiennes

Exp./Trigo.

Définition cartésienne

Coordonnées M

Affixe de

(x,y)

z = x + iy

Définition polaire

Coordonnées M

Affixe de

Z = X = iY

Exponentiel / Trigonométrie

Voir exemple application de la relation de Chasles / Cartésien / Polaire

Invention du vecteur

J'appelle somme géométrique d'un nombre quelconque de lignes a, b, c … données en grandeur, direction et sens, une ligne égale et parallèle au dernier côté d'un polygone dont les autres côtés sont a, b, c .. placés bout à bout, chacun dans son sens propre.

Saint-Venant, comptes rendus de l'Académie des sciences en 1845

Anglais

Vector: The term vector is used to describe a quantity
that has a magnitude and a direction.

A point of application is not of concern in mathematics, while it does matter in physics.

A vector is an ordered pair consisting of a positive real number, the magnitude or length, and a direction in space.

The vectors a and b are said to be equal if they have the same magnitude and the same direction.

Relation de Chasles
Relation de Chasles	J'ajoute autant de points intermédiaires que je veux.
Exemple Flèches des vecteurs omises.	Simplifier. 2AB + BC + BD = AB + BC + AB + BD = AC + AD
Exemple Rappel de construction de la somme de vecteurs.	Exprimer AM à partir de cette figure AM + 2BA – 3CA = 0 AM = –2BA + 3CA AM = 2AB – 3AC Avec AB et AC dans le résultat, nous serions tentés de chercher une simplification en CB par relation de Chasles. Pas possible et cette construction montre que nous ne pouvons pas aller plus loin dans l'expression de AM. Il est tout de même possible de tenter quelque chose. AM = 2AB – 2AC – AC AM = 2 (AB – AC) – AC AM = 2 (CA + AB) – AC AM = 2 CB – AC Nous venons de permettre la construction de AF par un autre chemin. pas plus, pas moins.

Voir Relation de Chasles avec les angles orientés

Produit scalaire et déterminant
Nom	Produit scalaire	Déterminant
Valeur simple formel
Représente	Projection k est la projection de v sur u	Aire du parallélogramme
Idée	k = 0 si v est perpendiculaire à u	h = 0 si v est couché sur u; v et u sont colinéaires
Calcul cartésien	xx' + yy' =	xy' – x'y =
Cas particulier
… Sinon	ORTHOGONALITÉ	COLINÉARITÉ Voir Colinéarité
Anglais	Scalar product Vector projection k	Determinant Vector product

Anglais: dot product

Produit scalaire – Résumé
Repère orthonormé direct
Deux vecteurs
Définition du produit scalaire

Propriétés

Voir Démonstration vectorielle du théorème de Pythagore
Produit scalaire et orthogonalité en algèbre linéaire

Produit vectoriel

Le produit vectoriel de deux vecteurs est le vecteur:

orthogonal au deux premiers;

la base est directe (les trois vecteurs u, v et w s'enchaînent comme en vissant); et

le module est donné par la formule en sinus.

Le produit vectoriel de deux vecteurs colinéaires est nul par définition.

Anglais: cross product

Produit vectoriel – Résumé
Repère orthonormé direct
Deux vecteurs
Définition du produit vectoriel – DIRECTION	Perpendiculaire au plan formé par les vecteurs
Définition du produit vectoriel – SENS	Règle des trois doigts (main droite)
Valeur
Norme du produit vectoriel = Aire du parallélogramme (vert sur la figure)			est directement perpendiculaire au plan
Propriétés			Le produit vectoriel de deux vecteurs colinéaires est nul.




Scalaire et vectoriel M volume du parallélépipède		Ce volume (orienté ou signé) correspond au déterminant de la matrice carrée formée par (a,b,c).
Mnémotechnique du produit mixte	Faire ce tableau En positif les trois diagonales de type jaune en a₁, b₁ et c₁: a₁b₂c₃+b₁c₂a₃+c₁a₂b₃; En négatif, les trois diagonales de type rose a₁, b₁ et c₁: a₁b₃c₂+b₁c₃a₂+c₁a₃b₂.