|
||||||||||||||||||||||||||||||||||
![]()
|
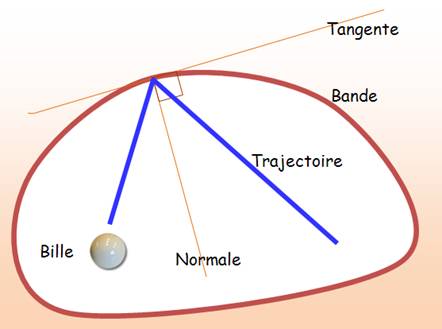
BILLARD La
boule de billard rebondit sur les bords de la table de billard comme un rayon
lumineux se réfléchit sur un miroir. Elle obéit aux mêmes lois la trajectoire
réfléchie. |
Voir Réflexion
|
Deux copains se retrouvent. L'un d'eux est accompagné d'une grosse mite et d'un génie tourbillonnant
autour de lui. -
Pour fêter nos retrouvailles, je te laisse faire
un vœu; mon génie l'exaucera. -
D'accord! je voudrai un milliard. Alors, un beau billard apparaît devant lui. -
Il est sourd lui; je n'ai pas demandé un milliard, pas un billard. -
Qu'est-ce tu crois que j'ai vraiment demandé moi
… |
Voir Pensées & humour

|
|
|
|
Types de jeux de billard Billard français Jeu de carambolage
Billard anglais
Six blouses. Billard américain (american pool)
Six blouses. Table dite 9 pieds (9ft): 2,54m x 1,27 m x 0,76 m. Jeu du huit – majorité des pubs anglais et le plus commun dans le monde:
Billes
1 à 7 au second joueur; Bille 8, noire, n'est pas attribuée; et Billes
9 à 15 au premier joueur. Six blouses. Paquet de 15 billes en triangles. il
faut empocher toutes les billes de son groupe et finir par la noire. Snooker
|
|
|
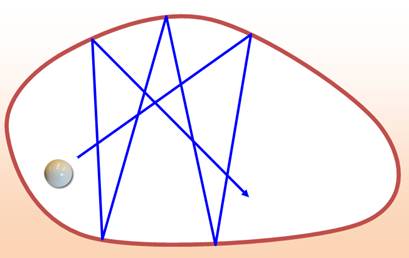
Faire
un trois-bandes: la bille doit rebondir au
moins trois fois sur les
rebords. |

|
|
||
|
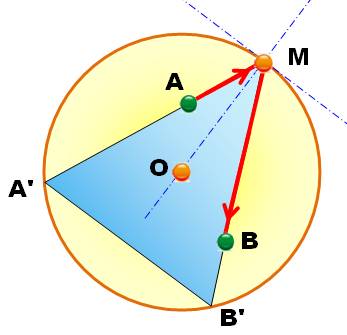
Problème Un billard
circulaire et deux billes A et B placées en deux points quelconques. La bille
A doit rebondir une fois et atteindre la boule B. Où se
trouve le point de rebond? Il s’agit
de la trajectoire d'un rayon lumineux reliant un point à un autre après
réflexion sur un
miroir circulaire. Autres formulations Trouvez
un triangle isocèle inscrit dans un cercle et passant par deux points donnés.
De deux
points dans un cercle, trouvez les droites qui se croisent sur le cercle avec
le même angle par rapport à la tangente en ce point d'intersection. Solution Une
équation du quatrième degré
(biquadratique) du type:
La
solution est non constructible
avec règle et compas car elle nécessite l'extraction d'une racine cubique. Généralisation Cas de
miroirs paraboliques, hyperboliques ou elliptiques. Alors, la solution
nécessite la résolution d'une équation du huitième degré. Anglais Given a light source and a spherical
mirror, find the point on the mirror were the light will be reflected to the
eye of an observer. |
Ptolémée (vers100- vers 170) Ptolémée
est le premier à formuler ce problème en l'an 150. Alhazen Alhazen
traite de cette question dans son traité d'optique. Il trouve une solution
géométrique impliquant les sections coniques, et non par calcul
algébrique. Léonard de Vinci (1452-1519) Léonard de
Vinci le résout avec un système articulé. Autres mathématiciens Christiaan Huygens, James Gregory, Guillaume de l'Hôpital, Isaac
Barrow et bien d'autres se sont
essayés à la résolution de ce problème; tentant l'utilisation de méthodes
analytiques, géométriques, dérivation ou nombres complexes. Peter M. Neumann En 1997, ce professeur à
Oxford, donne la solution: Cette preuve apporta la
solution au dernier problème de géométrie classique. |
|
Ibn al-Haytham Alhazen (Bassora, 965 – Le Caire,
1039)
|
Vari nom:
Abu Ali al-Hasan ibn al-Haytham, plu connu sous le
nom: Alhazen, version latine de al-Hasan Alhazen (illustration) est un physiologiste et
physicien musulman de l’époque médiévale. Il fut l’un
des premiers promoteurs de la méthode expérimentale en sciences, tout en
utilisant les mathématiques pour assoir la physique théorique. Il
s’illustre par ses travaux fondateurs dans les domaines de l’optique
géométrique et physiologique. Très
estimé de la communauté scientifique, Alhazen a devancé de quelques siècles
plusieurs découvertes faites par des scientifiques européens pendant la
Renaissance. Il
influença grandement Roger Bacon et Johannes Kepler. |
Source: France culture – Alhazen,
la science au Moyen Âge – 21/01/2018

|
|
|
|
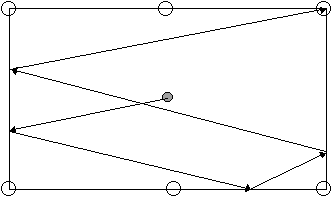
La boule au centre doit être lancée sans effet. Il
faut la faire sortir en 4 bandes (4 rebonds sur les bords)
|
|

|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voici
quelques exemples : Ligne
de visée :
Valeurs
numériques :
v1 = v0 cos a1
et v2 = v0 sin a1
Théorie :
m
v0² = m v1² + m v2²
m v0 = m v1
+ m v2
v0 = v1
cos a1 + v2 cos a2 0 = v1 sin
a1 - v2 sin a2
cos
(a1 + a2) = 0 => a1 + a2 =
90°
v2 = v1
sin a1 / sin a2 v0 = v1
(cos a1 + sin a1 . cos a2 / sin a2 )
cos a2 = sin a1 et sin a2
= cos a1
v1 (cos² a1
+ sin² a1 ) / cos a1 = v1
/ cos a1 = v0
v1 = v0
cos a1 et v2 = v0
sin a1 Attention :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
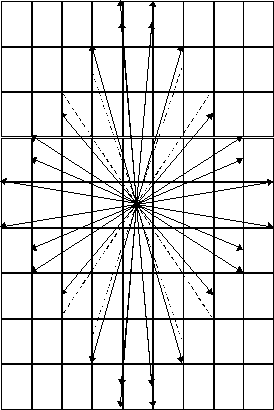
la bille fait q rebonds et p tours avant de
revenir sur la même trajectoire. Dans
la réalité
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Pour les experts
|
|
Cette page |
![]()