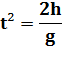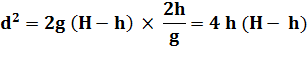|
||||||||||||||||||||||||||||
![]()
|
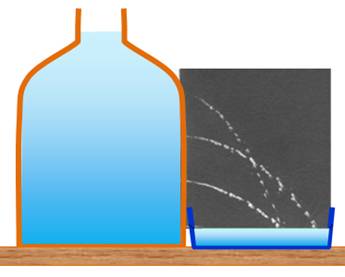
Bouteille percée Tonneau percé Trois trous dans la bouteille Expérience assez classique
en physique: faire des trous dans une bouteille en plastique et observer les
jets produits lorsque la bouteille est remplie d'eau. Encore un cas où
l'intuition, le sens commun, est mis à mal. Il semblerait que les sites
proposent une interprétation sans aller au bout de l'explication du
phénomène. Cette page a été réalisée
sur la base des artiches en anglais cités en référence. |
Anglais: Three-holes bottle
|
|
||
|
La
pression de l'eau est de plus en plus élevée avec la profondeur. Normal! La
masse d'eau au-dessus est de plus en plus grande. L'eau qui
se trouve au fond de la bouteille est soumise à la plus forte pression. Ce qu'il
faut savoir:
p = g .
h . d (g étant
l'accélération de la pesanteur).
|
||
|
Prendre une bouteille en plastique
(ou une brique (pack) de jus de fruit ou de lait). Percez trois ou quatre
trous à différents niveaux. Versez de l'eau dans la
bouteille et observez les trajectoires des filets d'eau. Améliorer l'effet en
masquant les trous avec du ruban adhésif que vous retirerez lorsque la
bouteille sera pleine. Le problème consiste à
déterminer à quelle distance chaque trou va émettre son jet. |
Anglais: Three-holes bottle: in a
fluid at rest, hydrostatic pressure increases with depth. |
|
|
|
|
|
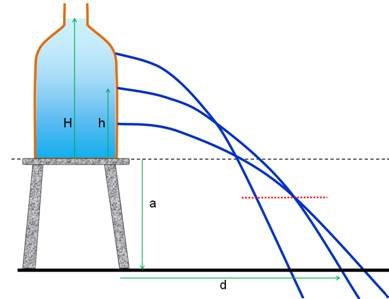
Illustration
Trajectoires paraboliques à la sortie des trous dans la bouteille. Le trait rouge matérialise la base de la bouteille. Source
photo: Le tonneau percé
(vidéo) |
|
|
|
||
|
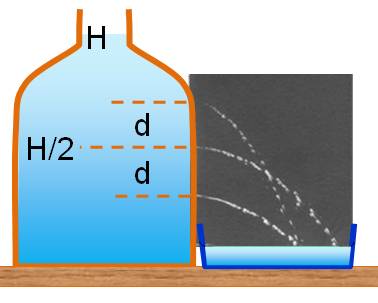
Le jet le plus lointain est
obtenu pour un trou à mi-hauteur d'eau. Les jets de deux trous
équidistants du milieu se retrouvent au même endroit. On pourrait penser que la
pression grandissant, le jet devrait aller de plus en plus loin en faisant le
trou de plus en plus bas. Or, c'est faux! Pensez à un
jet à la base. Il est évident qu'il ne peut pas aller bien loin! Même Léonard de Vinci
s'était fait prendre. Par contre, Torricelli vers 1640 a eu la bonne vision Alors? |
|
|
|
Supposons le liquide non
visqueux et appliquons le théorème de Daniel Bernoulli (1738). Torricelli fut le premier en
1636 à trouver cette relation qui est un cas particulier du théorème de
Bernoulli. |
H est la hauteur totale du liquide; h est la hauteur où se trouve la perforation; g l'accélération
de la pesanteur; et v(h) la vitesse
d'expulsion. |
|
|
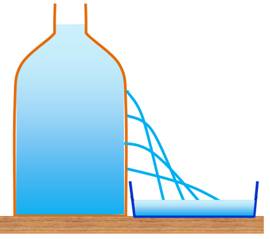
Si la distance
d'atterrissage d du jet ne
dépendait que de la vitesse de sortie alors, plus le trou est bas, plus le
jet irait loin. |
Image classique,
erronée. |
|
|
|
||
|
Le paramètre qui ne doit pas
être ignoré est le temps de vol libre du jet (t). Plus le trou est placé haut et plus le temps de vol est
grand. |
|
|
|
En supposant le jet horizontal
à la sortie du trou, la distance est égale à la vitesse multipliée par
le temps. |
|
|
|
Remarquez la symétrie en h et H –
h qui implique que deux trous, l'un en h et l'autre en H – h provoqueront des
jets qui tomberont au même endroit. |
|
|
|
Si la surface horizontale
d'atterrissage est situé plus bas, à une distance a suffisante (trait pointillé rouge) le jet du bas peut
éventuellement dépasser les deux autres en distance. La situation serait la même
si la bouteille se prolongeait jusqu'à la nouvelle surface horizontale. Notez
que le point milieu vient donc de changer de place. |
|
|
|
On vient simplement de
changer les paramètres géométriques les hauteurs sont augmentée de a, et la distance s'exprime par la
nouvelle formule. |
|
|
Bilan
|
L'expérience
montrée dans les livres ou sur Internet est insuffisamment expliquée. De
toute façon, l'observation du phénomène est délicate. Seule des mesures en
laboratoire permettent de cerner la réalité qui s'avère particulièrement
sensibles aux conditions de réalisation de l'expérience. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Livre |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/PRESSION/Bouteill.htm
|