|
|||||||||||||||||||||||||||||||||
![]()
|
Pompage et pression atmosphérique Expérience de Torricelli Baromètre Sans doute pour certains une
découverte: l'explication surprenante d'un geste banal, boire à la paille. Et
aussi intrigant, l'explication du fonctionnement du siphon. |
|
|
||
|
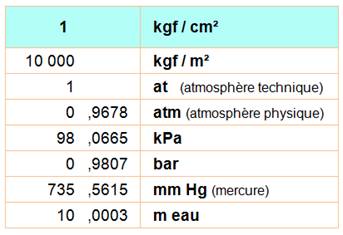
Prenons la pression atmosphérique telle
qu'indiquée sur ce tableau avec ses équivalences. Elle correspond à la
pression atmosphérique moyenne au niveau de la mer sous nos latitudes Au détail près
de la distinction entre atmosphère physique et atmosphère technique que nous
négligerons ici >>> |
Voir Unités de pression |
|
|
Imaginons un tube de 1 cm²
de section, par exemple. Prenons une longueur de tube
telle qu'il contienne un kg de matière. Le tube étant positionné
verticalement, nous aurons la même pression à la base d'un tube rempli:
|
|
|
|
|
||
|
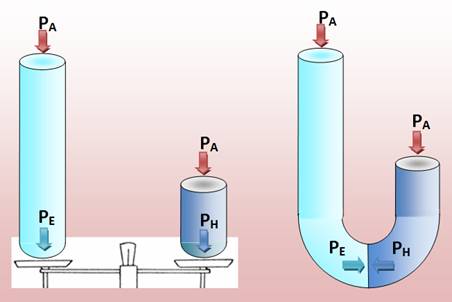
Le tube-eau sur un plateau
d'une balance et le tube-mercure sur l'autre, il y a équilibre, y compris en
ajoutant de chaque côté le poids inévitable de l'air (pression
atmosphérique). Il en va de même si nous raccordons
les deux tubes: le poids de l'un équilibre le poids de l'autre. En versant le même volume
d'un liquide d'un côté du tuyau et d'un autre liquide de l'autre côté (non
miscibles), chacun prend une hauteur différente selon sa masse volumique
(densité). |
|
|
|
On vient de montrer comment équilibrer
l'eau et le mercure. Continuons: comment équilibrer la colonne d'air avec une
colonne de mercure? C'est l'expérience de Torricelli (1643) et l'invention du
baromètre, instrument qui permet de peser l'air de l'atmosphère que nous supportons. Torricelli (1608-1647) est alors le
secrétaire de Galilée, à qui il
succèdera comme professeur de philosophie et de mathématiques.
|
Voir Historique (suite)
|
|
||
|
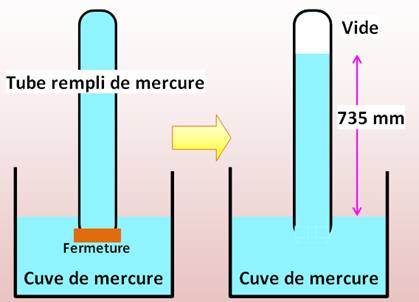
Une cuve contenant du mercure. Un tube de verre de un mètre de
long, fermé à une extrémité et rempli de mercure. L'autre extrémité est fermée
momentanément (bout de carton) et elle est plongée dans la cuve. Le couvercle
en carton est retiré. Alors le mercure s'affaisse
dans le tube en une colonne de 735 mm de haut (760 mm
si nous avions pris l'atmosphère physique. Tout dépend du lieu et des conditions
de l'expérience). |
Attention: la manipulation du mercure est dangereuse! |
|
|
Dans le haut du
tube, outre quelques vapeur de mercure, s'est créé du vide (pas d'air! d'où
viendrait-il?). Ce n'est pas le
vide qui retient le mercure de descendre complètement. Il ne retient rien. C'est la
pression atmosphérique qui pousse. |
L'équilibre est réalisé entre la pression atmosphérique sur la surface
du mercure dans la cuve et le poids de la colonne de mercure dans le tube. Sur ce principe, il invente le baromètre. |
|
|
1er siècle,
Héron d'Alexandrie: première pompes aspirantes. "Ainsi, que l’on prenne un vase léger à ouverture
étroite et qu’on l’applique contre les lèvres en aspirant l’air, ce qui le
raréfie, le vase restera suspendu aux lèvres, car le vide attirera la chair
dans le vase afin de remplir le vide. Il est donc clair que la portion de
l’espace compris dans le vase était devenue vide en partie." Héron 1630,
Jean-Baptiste Baliani suggère l'hypothèse de la pression atmosphérique, sans
la valider. 1638,
Galilée constate qu'effectivement l'eau ne montera pas au-dessus de dix-huit
coudées. "Sagredo: Ce qui est attiré dans la pompe,
n’est-il pas, en somme, un cylindre d’eau qui, attaché par en haut, s’allonge
de plus en plus, atteignant finalement ce point au-delà duquel, tiré par son
propre poids devenu excessif, il se rompt exactement comme une
corde". Galilée 1641,
Magiotti et Bertie mettent en place l'expérience pour confirmer l'impossibilité de monter
l'eau à plus de 10,33 m. 1643,
Torricelli (avec Viviani) imagine une expérience plus simple avec du mercure.
Il confirme par l'expérience l'explication de ce phénomène. "Pour Torricelli (comme pour Baliani; Berti
ou Magiotti), la limite atteinte par la colonne de mercure dans le tube
correspond à une situation d’équilibre entre le poids de cette colonne et le
poids de l’air situé au-dessus de la surface du mercure du récipient". Cécile
Hosson Par peur de l'Inquisition qui avait sévi pour
Galilée, il ne publie pas ses résultats. La nouvelle se répand tout de même (Mersenne). 1648,
Pascal et son expérience du Puy-de-Dôme: il montre l'influence de l'altitude
sur la hauteur de mercure. Pascal vient d’apporter la preuve de l’existence
de la pression atmosphérique et il fondait l’hydrostatique. " La nature n’a aucune répugnance pour le
vide ; elle ne fait aucun effort pour l’éviter ; tous les effets qu’on a attribués
à cette horreur procèdent de la pesanteur et pression de l’air ; elle en est
la seule et véritable cause, et, manque de la connaître, on avait inventé
exprès cette horreur imaginaire du vide, pour rendre raison. " Pascal 1654, Otto
von Guericke et les sphères de Madebourg. Deux demi-sphères couplées, le vide
à l'intérieur. Deux attelages de 8 chevaux essayèrent sans succès de séparer
les deux demi-sphères en tirant chacun de son côté. Démonstration de
l’existence de la pression atmosphérique et de la force qu’elle peut
représenter. 1660, Robert
Boyle réalise une pompe à vide et y reconduit l'expérience de Torricelli. Le
niveau du mercure baisse au fur et à mesure du vide créé. Mariotte fera cette
expérience (1676) en immersion sous l'eau. |
D'après
notemment: Une
reconstruction historique du concept de pression atmosphérique – Cécile
Poisson
|
|
||
|
Prenons un verre d'orangeade
que nous sirotons avec une paille. Fausse explication Le sens
commun dirait que l'aspiration fait monter le liquide dans la paille. Ce
n'est pas la bonne explication! C'est celle qui prévalait avant Torricelli,
au motif que la nature a horreur du vide. C'était comme si, le liquide
s'accrochait à l'air aspiré. Dans le cas où cette colonne de liquide devenait
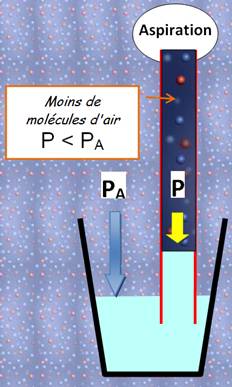
trop grande, on expliquait qu'il y avait décrochement ou cassure de la colonne. Vraie explication C'est la
pression de l'atmosphère à l'autre bout qui pousse. Lorsque nous aspirons,
nous créons un manque d'air (il y a moins de molécules d'air), absence qui va
être comblé par le liquide poussé de l'autre côté (PA). En
aspirant, la pression de l'air (P) dans la paille est réduite (dépression):
moins de molécules donc moins de poids. Dans le verre, la pression de l'air
(PA) sur la surface du liquide cherche à rétablir l'équilibre. Le
liquide monte dans la paille. En aspirant,
nous ne créons pas une pression négative qui attirerait le liquide, mais une
pression moindre qui est vite compensée. |
|
|
Voir Forces et
équilibre
|
|
||
|
Nous
nous intéressons à un cas où la paille est géante, nécessitant
une pompe mécanique pour aspirer. |
||
|
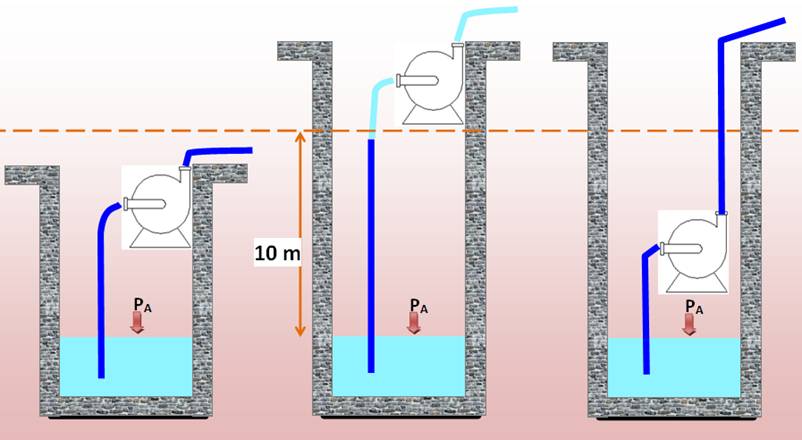
Un puits
et une pompe aspirante. Tant que la
hauteur entre le niveau de l'eau et le tuyau d'admission est inférieure à 10
mètre la pompe fonctionne. La
pression atmosphérique est suffisante pour pousser l'eau et combler le vide
d'air crée par la pompe. |
Si la
hauteur dépasse les 10 mètres, la pression de l'atmosphère n'est plus
suffisante pour faire grimper l'eau. La pompe
fait son boulot en dégageant de la place libre d'air, mais la seule force
agissante pour y faire monter l'eau est la pression atmosphérique. Elle n'est
pas à la "hauteur". |
|
|
Avec une hauteur de plus de 10 mètres, impossible de
faire fonctionner une pompe aspirante; possible avec une pompe refoulante
tant que celle-ci se trouve en-dessous des 10 m. Une pompe de dénoyage
(utilisation dans les mines), sous 16 atmosphères, peut refouler l'eau
jusqu'à 150 mètres de haut. |
||
|
La hauteur théorique n'est jamais atteinte du fait de
frottements. Avec l'altitude, cette hauteur maximale décroit d'environ
0,125 m pour 100 m de plus en altitude. Pour 1500 m, hmax = 10,33 – 15 x
0,125 = 10,33 – 1, 875 = 8,455 m. La pression atmosphère joue proportionnellement. Si p = 980
millibars, alors que la pression atmosphérique normale est 1013 mbar, hmax =
10,33 x 980 / 1013 = 9,993 m La température joue également un rôle. À 50°C, la hauteur
maximale chute de 1,3 m |
|
|
||
|
Deux explications sont
avancées: |
Two competing models have
emerged. In one model, water flowing out of a siphon generates a low-pressure
region at the crown so that atmospheric pressure
pushes water into the siphon. In another, the weight of water flowing out of
a siphon pulls water into the siphon via liquid
cohesion. |
|
|
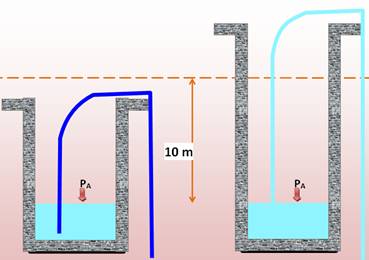
Explication commune La plupart du temps
l'explication donnée est comparable à celle donnée pour les fontainiers. La
conclusion est alors qu'il est impossible de siphonner à plus de 10 m. Comme pour un train qui
suivrait le chemin de l'eau, lorsque les wagons descendants sont plus
nombreux que les wagons montants, la gravité
joue et met en mouvement l'ensemble. Cependant avec cette explication les
wagons ne sont pas attachés, c'est la pression atmosphérique qui pousse le
dernier. |
On dit généralement qu'il serait impossible de
siphonner avec un coude d'une hauteur de plus de 10 m. Ce n'est pas vrai. |
|
|
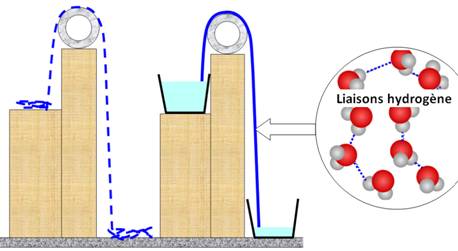
Explication alternative C'est également la gravité
qui est en jeu, conjuguée avec les liaisons hydrogène de l'eau
qui relient les wagons. Ici, l'analogie de la chaîne
est pertinente: le poids de la chaine est plus important à droite qu'à
gauche, et malgré le frottement sur la poulie, la chaine descend sur le sol. |
|
|
|
L'eau qui passe dans le
tuyau du siphon est en fait une longue chaine de milliards de molécules d'eau
"enchainées" par leurs liaisons hydrogène. L'énergie nécessaire pour
faire monter l'eau est largement compensée par la force gravitationnelle (le
poids) qui règne dans la partie descendante. Et, il est vrai que plus la cuve
réceptrice est basse et plus le débit est important. Ce phénomène est bien connu: c'est celui qui fait
monter la sève dans les arbres et ce , naturellement, à beaucoup plus de
10mètres. La hauteur maximale du coude
peut dépasser les 10 m. Elle ne dépend que de la tension superficielle que
l'eau peut supporter, la tension maximum que peut supporter la liaison
hydrogène. L'atmosphère joue son rôle classique en facilitant le phénomène et
en augmentant légèrement la hauteur maximum. Le débit de l'eau (v) dépend
donc de la seule hauteur (h), entre l'entrée et la sortie de l'eau.
Formule dérivée de l'équation de Bernoulli, et
qui peut simplement se déduire des formules classiques: à quelle vitesse une
balle lancée d'une hauteur h arrive-t-elle au sol? Voir le calcul >>> |
||
|
|
||
|
La girafe a un long cou.
Comment fait-elle pour boire. Du sol à son estomac, l'eau doit subir un
dénivelé d'environ 2 mètres. |
Aspiration comme avec une paille? Non. Aspiration dans la bouche et remonter la tête pour faire descendre l'eau dans l'estomac par gravité ? Presque. Autre phénomène? Oui. |
|
|
Compte tenu de la pression
atmosphérique, il est impossible d'aspirer sur une hauteur supérieure à 10
mètres. En pratique, l'homme est incapable d'aspirer dans une paille de plus
de 6 mètres. |
Pour s'abreuver, elle adopte une position curieuse due au fait que ses
pattes son raides. Notez que sa tête peut se mouvoir sur 5 mètres en altitude. Il lui faut
un coeur solide (environ 12 kg) pour gérer la pression sanguine |
|
|
La girafe fonctionne comme
si elle était dotée d'une pompe à refoulement. |
La girafe aspire l'eau par succions succesives et, par le jeu
d'ouvertures et fermetures de l'œsophage, elle remplit son œsophage (environ
5 litres). Puis, elle redresse son cou et laisse agir la gravité. Un mouvement de la machoire inférieure réduit la cavité buccale et
pousse l'eau dans l'œsophage. |
|
D'après La girafe, la
paille et la pompe à piston – Jean-Michel Courty et Édouard Kierlik – Pour la
Science – Juin 2016
|
Le baromètre fonctionne en équilibrant le
poids de l'air de l'atmosphère avec le poids d'une colonne de mercure.
Aspirer de l'eau n'est possible que parce que la pression atmosphérique
"pousse" la surface de l'eau de l'autre côté. Aspirer de l'eau (ou
autres liquides) est possible mais jusqu'à une certaine limite atteinte
lorsque le poids de la colonne d'eau est égal à la pression atmosphérique.
Quant au siphon, l'explication n'est pas encore stabilisée: est-ce l'effet de
la pression atmosphérique ou bien une sorte de cohésion des molécules
d'eau? |
|
Expérience
de Torricelli Ce que je ne comprends pas dans cette
expérience ce n’est pas pourquoi le mercure ne tombe pas plus bas que 0,76m
mais au contraire pourquoi il tombe? La
pression atmosphérique n’a pas lieu sur le haut du tube étant donné que
celui-ci est fermé, je vois ça un peu comme le fait de remplir une paille
avec de l’eau et de boucher l’extrémité supérieure, l’eau ne s’écoule pas car
il n’y a pas de pression atmosphérique. Et donc, je ne vois pas pourquoi là,
le mercure s’échappe vers le bas pour après se stabiliser au 0,76 m. Explications 1)
Je bois à la paille: lorsque j'aspire je pompe les molécules d'air, je crée
du vide. À l'autre bout dans le verre, la pression atmosphérique pousse et
fait monter l'orangeade dans la paille. Ce n'est pas moi qui aspire la
boisson. La boisson occupe l'espace libéré sous l'effet de la pression
atmosphérique à l'autre bout de la paille. 2)
Je mets de l'eau dans une paille et bouche l'extrémité. Le poids de cette
petite quantité d'eau n'est pas suffisant pour compenser la pression
atmosphérique. C'est elle qui gagne. Il faudrait une paille de plus de 10
mètre de haut. Alors, son poids serait suffisant pour vaincre la pression
atmosphérique. Notez que la pression atmosphérique agit dans tous les sens
comme lorsque vous êtes dans l'eau, vous ressentez la pression partout. C'est
la même chose avec l'air. C'est pourquoi, la pression atmosphérique agit même
sur l'extrémité inférieure de la paille. 3)
Dans l'expérience de Torricelli, avec 76 cm, le mercure est suffisamment
pesant pour équilibrer la pression atmosphérique. Dans le haut du tube se
crée un petit espace vide, du "rien"! En fait quelques molécules de
vapeur de mercure. Si le tube était ouvert, la pression agirait sur le
mercure dans le tube comme dans la cuve. Le mercure se mettrait au même
niveau (principe des vases communicants). Pour bien comprendre, imaginons par
la pensée que l'expérience se fasse dans un monde ou règne le vide complet.
Un tube en U. Dans la première branche du U versons de l'air et dans l'autre
du mercure. D'un côté, il faudra 76 cm de mercure et de l'autre 10 à 20 km
d'air (l'épaisseur de l'atmosphère) pour équilibrer le poids du mercure. 4)
Expérience du verre: de l'eau mais sans remplir. Le verre est recouvert par
une plaque de carton et mis tête en bas (manipulation délicate à réussir). La
feuille reste collée et l'eau ne tombe pas. Par contre, si on retire le
carton, l'eau ne tient pas en équilibre, et se répand au sol. L'explication
est délicate. Elle tient au fait que le haut du verre contient de l'air et
non du vide comme avec la paille en 2). Explication détaillée dans: Des
fluides sens dessus dessous – Pour la Science n°467 de septembre 2016. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Livre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/PRESSION/Pompe.htm |