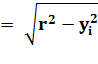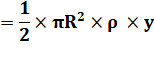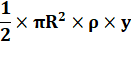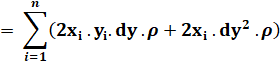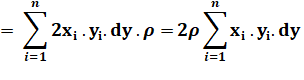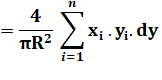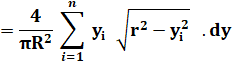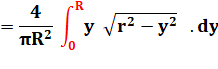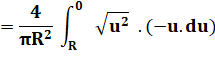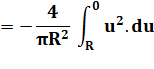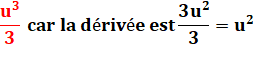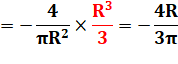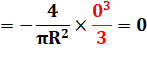|
||||||||||||||||||||||||||||||
![]()
|
Centre de gravité Calcul pour formes complexes Plus que la forme, c'est le
calcul qui s'avère complexe. Il fait appel au principe d'équivalence et aux
calculs de sommes infinies (intégration). Nous allons aborder cela simplement, sans les bagages du calcul
intégral. |
|
|
||
|
|
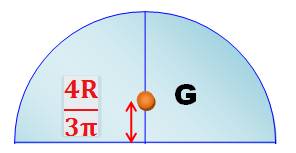
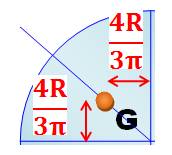
4 / 3Pi =
0,4244… Voici les coordonnées
du centre de gravité du demi-cercle ou du quart de
cercle. Comment les calculer? Oui! Il faut dire disque lorsque le cercle est plein. |
|
|
|
||||
|
|
||||
|
|
|
|||
|
|
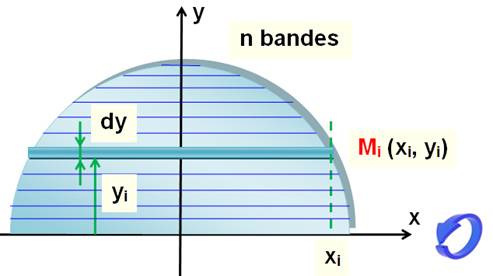
r² |
= xi² + yi² |
||
|
|
xi |
|
||
|
|
mi |
|
||
|
|
di |
= yi + dy |
||
|
|
||
|
|
y |
|
|
|
u² |
= r² – y ² |
|
|
2u.du |
= 0 – 2y. dy |
|
|
u |
varie de r
à 0 |
|
|
y |
|
|
|
||
|
|
u² |
|
|
|
yR |
|
|
|
y0 |
|
|
|
yG |
|
Voir Calcul par intégrales / Primitives
|
Le centre de gravité
ou centre géométrique du demi-disque est situé sur l'axe de symétrie à une
distance du centre de 4R
/ 3Pi = 0,4244131815783875620503567023267…
R Soit, un peu
en-dessous du milieu du rayon. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/STATIQUE/CGFormCo.htm
|